Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
ESPERET, LOUIS
and
JORET, GWENAËL
2014.
Colouring Planar Graphs With Three Colours and No Large Monochromatic Components.
Combinatorics, Probability and Computing,
Vol. 23,
Issue. 4,
p.
551.
Esperet, Louis
and
Ochem, Pascal
2016.
Islands in Graphs on Surfaces.
SIAM Journal on Discrete Mathematics,
Vol. 30,
Issue. 1,
p.
206.
Axenovich, Maria
Ueckerdt, Torsten
and
Weiner, Pascal
2017.
Splitting Planar Graphs of Girth 6 into Two Linear Forests with Short Paths.
Journal of Graph Theory,
Vol. 85,
Issue. 3,
p.
601.
Abreu, Marién
Goedgebeur, Jan
Labbate, Domenico
and
Mazzuoccolo, Giuseppe
2018.
A note on 2-bisections of claw-free cubic graphs.
Discrete Applied Mathematics,
Vol. 244,
Issue. ,
p.
214.
Abreu, Marién
Goedgebeur, Jan
Labbate, Domenico
and
Mazzuoccolo, Giuseppe
2019.
Colourings of cubic graphs inducing isomorphic monochromatic subgraphs.
Journal of Graph Theory,
Vol. 92,
Issue. 4,
p.
415.
Anastos, Michael
and
Bal, Deepak
2020.
A Ramsey property of random regular and k‐out graphs.
Journal of Graph Theory,
Vol. 93,
Issue. 3,
p.
363.
Cheng, Shuting
Wu, Baoyindureng
and
Tramontana, Fabio
2021.
On the
k
-Component Independence Number of a Tree.
Discrete Dynamics in Nature and Society,
Vol. 2021,
Issue. ,
p.
1.
Das, S.
Pokrovskiy, A.
and
Sudakov, B.
2021.
Isomorphic bisections of cubic graphs.
Journal of Combinatorial Theory, Series B,
Vol. 151,
Issue. ,
p.
465.
Liu, Chun-Hung
and
Wood, David R.
2022.
Clustered variants of Hajós' conjecture.
Journal of Combinatorial Theory, Series B,
Vol. 152,
Issue. ,
p.
27.
Dujmović, Vida
Esperet, Louis
Morin, Pat
Walczak, Bartosz
and
Wood, David R.
2022.
Clustered 3-colouring graphs of bounded degree.
Combinatorics, Probability and Computing,
Vol. 31,
Issue. 1,
p.
123.
Dujmović, Vida
Esperet, Louis
Morin, Pat
and
Wood, David R.
2023.
Proof of the Clustered Hadwiger Conjecture.
p.
1921.
Liu, Chun-Hung
2023.
Immersion and clustered coloring.
Journal of Combinatorial Theory, Series B,
Vol. 158,
Issue. ,
p.
252.
Esperet, Louis
and
Wood, David R.
2024.
Colouring strong products.
European Journal of Combinatorics,
Vol. 121,
Issue. ,
p.
103847.
Liu, Chun-Hung
and
Wood, David R.
2024.
Clustered coloring of graphs with bounded layered treewidth and bounded degree.
European Journal of Combinatorics,
Vol. 122,
Issue. ,
p.
103730.
Distel, Marc
Dujmović, Vida
Eppstein, David
Hickingbotham, Robert
Joret, Gwenaël
Micek, Piotr
Morin, Pat
Seweryn, Michał T.
and
Wood, David R.
2024.
Product Structure Extension of the Alon–Seymour–Thomas Theorem.
SIAM Journal on Discrete Mathematics,
Vol. 38,
Issue. 3,
p.
2095.
Illingworth, Freddie
Scott, Alex
and
Wood, David
2024.
Product structure of graphs with an excluded minor.
Transactions of the American Mathematical Society, Series B,
Vol. 11,
Issue. 35,
p.
1233.
Dvořák, Zdeněk
and
Wood, David R.
2025.
Product Structure of Graph Classes with Strongly Sublinear Separators.
Innovations in Graph Theory,
Vol. 2,
Issue. ,
p.
191.
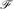 be any non-trivial minor-closed family of graphs. We show that mcc2(G) = O(n2/3) for any n-vertex graph G ∈
be any non-trivial minor-closed family of graphs. We show that mcc2(G) = O(n2/3) for any n-vertex graph G ∈ 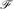 . This bound is asymptotically optimal and it is attained for planar graphs. More generally, for every such
. This bound is asymptotically optimal and it is attained for planar graphs. More generally, for every such 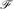 , and every fixed t we show that mcct(G)=O(n2/(t+1)). On the other hand, we have examples of graphs G with no Kt+3 minor and with mcct(G)=Ω(n2/(2t−1)).
, and every fixed t we show that mcct(G)=O(n2/(t+1)). On the other hand, we have examples of graphs G with no Kt+3 minor and with mcct(G)=Ω(n2/(2t−1)).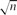 and n.
and n.
