Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kostochka, Alexandr
Mubayi, Dhruv
and
Verstraëte, Jacques
2015.
Turán problems and shadows I: Paths and cycles.
Journal of Combinatorial Theory, Series A,
Vol. 129,
Issue. ,
p.
57.
Verstraëte, Jacques
2016.
Recent Trends in Combinatorics.
Vol. 159,
Issue. ,
p.
83.
Gerbner, Dániel
and
Palmer, Cory
2017.
Extremal Results for Berge Hypergraphs.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 4,
p.
2314.
Füredi, Zoltán
and
Özkahya, Lale
2017.
On 3-uniform hypergraphs without a cycle of a given length.
Discrete Applied Mathematics,
Vol. 216,
Issue. ,
p.
582.
Maherani, L.
and
Shahsiah, M.
2018.
Turán Numbers of Complete 3-Uniform Berge-Hypergraphs.
Graphs and Combinatorics,
Vol. 34,
Issue. 4,
p.
619.
Jiang, Tao
and
Ma, Jie
2018.
Cycles of given lengths in hypergraphs.
Journal of Combinatorial Theory, Series B,
Vol. 133,
Issue. ,
p.
54.
COLLIER-CARTAINO, CLAYTON
GRABER, NATHAN
and
JIANG, TAO
2018.
Linear Turán Numbers of Linear Cycles and Cycle-Complete Ramsey Numbers.
Combinatorics, Probability and Computing,
Vol. 27,
Issue. 3,
p.
358.
English, Sean
Gerbner, Dániel
Methuku, Abhishek
and
Tait, Michael
2019.
Linearity of saturation for Berge hypergraphs.
European Journal of Combinatorics,
Vol. 78,
Issue. ,
p.
205.
Gerbner, Dániel
and
Palmer, Cory
2019.
Counting copies of a fixed subgraph in F-free graphs.
European Journal of Combinatorics,
Vol. 82,
Issue. ,
p.
103001.
Gerbner, Dániel
Methuku, Abhishek
and
Vizer, Máté
2019.
Generalized Turán problems for disjoint copies of graphs.
Discrete Mathematics,
Vol. 342,
Issue. 11,
p.
3130.
Gerbner, Dániel
Methuku, Abhishek
and
Vizer, Máté
2019.
Asymptotics for the Turán number of Berge-K2,.
Journal of Combinatorial Theory, Series B,
Vol. 137,
Issue. ,
p.
264.
Huang, Hao
and
Ma, Jie
2019.
On Tight Cycles in Hypergraphs.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 1,
p.
230.
Méroueh, Arès
2019.
The Ramsey number of loose cycles versus cliques.
Journal of Graph Theory,
Vol. 90,
Issue. 2,
p.
172.
Xu, Zixiang
Zhang, Tao
and
Ge, Gennian
2020.
Some tight lower bounds for Turán problems via constructions of multi-hypergraphs.
European Journal of Combinatorics,
Vol. 89,
Issue. ,
p.
103161.
Gerbner, Dániel
Nagy, Dániel T.
Patkós, Balázs
and
Vizer, Máté
2020.
$t$-Wise Berge and $t$-Heavy Hypergraphs.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 3,
p.
1813.
Gu, Ran
Li, Jiaao
and
Shi, Yongtang
2020.
Anti-Ramsey Numbers of Paths and Cycles in Hypergraphs.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 1,
p.
271.
Lu, Linyuan
and
Wang, Zhiyu
2020.
On the cover Ramsey number of Berge hypergraphs.
Discrete Mathematics,
Vol. 343,
Issue. 9,
p.
111972.
Gerbner, Dániel
Győri, Ervin
Methuku, Abhishek
and
Vizer, Máté
2020.
Generalized Turán problems for even cycles.
Journal of Combinatorial Theory, Series B,
Vol. 145,
Issue. ,
p.
169.
Gerbner, Dániel
Methuku, Abhishek
Omidi, Gholamreza
and
Vizer, Máté
2020.
Ramsey Problems for Berge Hypergraphs.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 1,
p.
351.
Spiro, Sam
and
Verstraëte, Jacques
2021.
Relative Turán numbers for hypergraph cycles.
Discrete Mathematics,
Vol. 344,
Issue. 10,
p.
112542.

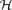 avoiding cycles of length 2
avoiding cycles of length 2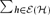 |
|