Hostname: page-component-89b8bd64d-shngb Total loading time: 0 Render date: 2026-05-08T01:57:28.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved Bounds for Incidences Between Points and Circles

Published online by Cambridge University Press:  02 October 2014

MICHA SHARIR ,
ADAM SHEFFER  and
JOSHUA ZAHL
MICHA SHARIR
Affiliation:
School of Computer Science, Tel Aviv University, Tel Aviv 69978, Israel (e-mail: michas@tau.ac.il, sheffera@tau.ac.il)
ADAM SHEFFER
Affiliation:
School of Computer Science, Tel Aviv University, Tel Aviv 69978, Israel (e-mail: michas@tau.ac.il, sheffera@tau.ac.il)
JOSHUA ZAHL
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90024, USA (e-mail: jzahl@mit.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish an improved upper bound for the number of incidences between m points and n circles in three dimensions. The previous best known bound, originally established for the planar case and later extended to any dimension ≥ 2, is O*(m2/3n2/3 + m6/11n9/11 + m + n), where the O*(⋅) notation hides polylogarithmic factors. Since all the points and circles may lie on a common plane (or sphere), it is impossible to improve the bound in ℝ3 without first improving it in the plane.

Nevertheless, we show that if the set of circles is required to be ‘truly three-dimensional’ in the sense that no sphere or plane contains more than q of the circles, for some q ≪ n, then for any ϵ > 0 the bound can be improved to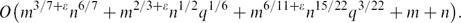

\[O\bigl(m^{3/7+\eps}n^{6/7} + m^{2/3+\eps}n^{1/2}q^{1/6} + m^{6/11+\eps}n^{15/22}q^{3/22} + m + n\bigr).\]
For various ranges of parameters (e.g., when m = Θ(n) and q = o(n7/9)), this bound is smaller than the lower bound Ω*(m2/3n2/3 + m + n), which holds in two dimensions.

We present several extensions and applications of the new bound.

  1. (i) For the special case where all the circles have the same radius, we obtain the improved bound O(m5/11+ϵn9/11 + m2/3+ϵn1/2q1/6 + m + n).

  2. (ii) We present an improved analysis that removes the subpolynomial factors from the bound when m = O(n3/2−ϵ) for any fixed ϵ < 0.

  3. (iii) We use our results to obtain the improved bound O(m15/7) for the number of mutually similar triangles determined by any set of m points in ℝ3.

Our result is obtained by applying the polynomial partitioning technique of Guth and Katz using a constant-degree partitioning polynomial (as was also recently used by Solymosi and Tao). We also rely on various additional tools from analytic, algebraic, and combinatorial geometry.

Keywords

Primary 52C10

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Issue 3 , May 2015 , pp. 490 - 520
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Agarwal, P. K., Apfelbaum, R., Purdy, G. and Sharir, M. (2007) Similar simplices in a d-dimensional point set. In Proc. 23rd ACM Symposium on Computational Geometry, pp. 232–238.CrossRefGoogle Scholar
[2]Agarwal, P. K., Matoušek, J. and Sharir, M. (2013) On range searching with semialgebraic sets~II. SIAM J. Comput. 42 2039–2062.Google Scholar
[3]Agarwal, P., Nevo, E., Pach, J., Pinchasi, R., Sharir, M. and Smorodinsky, S. (2004) Lenses in arrangements of pseudocircles and their applications. J. Assoc. Comput. Mach. 51 139–186.Google Scholar
[4]Akutsu, T., Tamaki, H. and Tokuyama, T. (1998) Distribution of distances and triangles in a point set and algorithms for computing the largest common point sets. Discrete Comput. Geom. 20 307–331.Google Scholar
[5]Alon, N. (1995) Tools from higher algebra. In Handbook of Combinatorics, Vols~1, 2, Elsevier, pp. 1749–1783.Google Scholar
[6]Apfelbaum, R. and Sharir, M. (2011) Non-degenerate spheres in three dimensions. Combin. Probab. Comput. 20 503–512.Google Scholar
[7]Aronov, B., Koltun, V. and Sharir, M. (2005) Incidences between points and circles in three and higher dimensions, Discrete Comput. Geom. 33 185–206.Google Scholar
[8]Aronov, B. and Sharir, M. (2002) Cutting circles into pseudo-segments and improved bounds for incidences. Discrete Comput. Geom. 28 475–490.CrossRefGoogle Scholar
[9]Basu, S. and Sombra, M. Polynomial partitioning on varieties and point–hypersurface incidences in four dimensions. arXiv:1406.2144.Google Scholar
[10]Beauville, A. (1996) Complex Algebraic Surfaces, second edition, Vol. 34 of London Mathematical Society Student Texts, Cambridge University Press.Google Scholar
[11]Bochnak, J., Coste, M. and Roy, M. (1998) Real Algebraic Geometry, Springer.Google Scholar
[12]Brass, P. (2002) Combinatorial geometry problems in pattern recognition. Discrete Comput. Geom. 28 495–510.Google Scholar
[13]Chazelle, B., Edelsbrunner, H., Guibas, L. J., Sharir, M. and Stolfi, J. (1996) Lines in space: Combinatorics and algorithms. Algorithmica 15 428–447.Google Scholar
[14]Cox, D., Little, J. and O'Shea, D. (2004) Using Algebraic Geometry, second edition, Springer.Google Scholar
[15]Cox, D., Little, J. and O'Shea, D. (2007) Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, third edition, Springer.Google Scholar
[16]Elekes, G., Kaplan, H. and Sharir, M. (2011) On lines, joints, and incidences in three dimensions. J. Combin. Theory Ser. A 118 962–977.Google Scholar
[17]Elekes, G. and Sharir, M. (2011) Incidences in three dimensions and distinct distances in the plane. Combin. Probab. Comput. 20 571–608.CrossRefGoogle Scholar
[18]Erdős, P. (1946) On sets of distances of n points. Amer. Math. Monthly 53 248–250.CrossRefGoogle Scholar
[19]Fox, J., Pach, J., Sheffer, A., Suk, A. and Zahl, J. A semi-algebraic version of Zarankiewicz's problem, arXiv:1407.5705.Google Scholar
[20]Fuchs, D. and Tabachnikov, S. (2007) Mathematical Omnibus: Thirty Lectures on Classical Mathematics, AMS.Google Scholar
[21]Fulton, W. (1998) Intersection Theory, Springer.Google Scholar
[22]Guth, L. Distinct distance estimates and low degree polynomial partitioning. arXiv:1404.2321.Google Scholar
[23]Guth, L. and Katz, N. H. (2010) Algebraic methods in discrete analogs of the Kakeya problem. Adv. Math. 225 2828–2839.CrossRefGoogle Scholar
[24]Guth, L. and Katz, N. H. On the Erdős distinct distances problem in the plane. Ann. of Math., to appear. arXiv:1011.4105.Google Scholar
[25]Harris, J. (1992) Algebraic Geometry: A First Course, Springer.CrossRefGoogle Scholar
[26]Hartshorne, R. (1983) Algebraic Geometry, Springer.Google Scholar
[27]Hartshorne, R. (2000) Geometry: Euclid and Beyond, Springer.Google Scholar
[28]Hwang, J. M. (2005) A bound on the number of curves of a given degree through a general point of a projective variety. Compositio Math. 141 703–712.Google Scholar
[29]Kaplan, H., Matoušek, J., Safernová, Z. and Sharir, M. (2012) Unit distances in three dimensions. Combin. Probab. Comput. 21 597–610.Google Scholar
[30]Kaplan, H., Matoušek, J. and Sharir, M. (2012) Simple proofs of classical theorems in discrete geometry via the Guth–Katz polynomial partitioning technique. Discrete Comput. Geom. 48 499–517.Google Scholar
[31]Kaplan, H., Sharir, M. and Shustin, E. (2010) On lines and joints. Discrete Comput. Geom. 44 838–843.Google Scholar
[32]Landsberg, J. M. (1999) Is a linear space contained in a submanifold? On the number of derivatives needed to tell. J. Reine Angew. Math. 508 53–60.Google Scholar
[33]Landsberg, J. M. (2003) Lines on projective varieties. J. Reine Angew. Math. 562 1–3.CrossRefGoogle Scholar
[34]Marcus, A. and Tardos, G. (2006) Intersection reverse sequences and geometric applications. J. Combin. Theory Ser. A 113 675–691.Google Scholar
[35]Matoušek, J. (2002) Lectures on Discrete Geometry, Springer.Google Scholar
[36]Milnor, J. (1964) On the Betti numbers of real varieties. Proc. Amer. Math. Soc. 15 275–280.CrossRefGoogle Scholar
[37]Miranda, R. (1995) Algebraic Curves and Riemann Surfaces, Vol. 5 of Graduate Studies in Mathematics, AMS.CrossRefGoogle Scholar
[38]Nilov, F. and Skopenkov, M. (2013) A surface containing a line and a circle through each point is a quadric. Geom. Dedicata 163 301–310.Google Scholar
[39]Pach, J. and Sharir, M. (2004) Geometric incidences. In Towards a Theory of Geometric Graphs (Pach, J., ed.), Vol. 342 of Contemporary Mathematics, AMS, pp. 185–223.Google Scholar
[40]Quilodrán, R. (2010) The joints problem in Rn. SIAM J. Discrete Math. 23 2211–2213.Google Scholar
[41]Roy, M.-F. and Vorobjov, N. (2002) The complexification and degree of a semi-algebraic set. Math. Z. 239 131–142.Google Scholar
[42]Salmon, G. (1915) A Treatise on the Analytic Geometry of Three Dimensions, Vol. 2, fifth edition, Hodges, Figgis and Co. Ltd., Dublin.Google Scholar
[43]Sard, A. (1942) The measure of the critical values of differentiable maps. Bull. Amer. Math. Soc. 48 883–890.Google Scholar
[44]Sharir, M. and Solomon, N. (2014) Incidences between points and lines in four dimensions. In Proc. 30th ACM Symposium on Computational Geometry, 189–197.Google Scholar
[45]Solymosi, J. and Tao, T. (2012) An incidence theorem in higher dimensions. Discrete Comput. Geom. 48 255–280.CrossRefGoogle Scholar
[46]Székely, L. (1997) Crossing numbers and hard Erdős problems in discrete geometry. Combin. Probab. Comput. 6 353–358.Google Scholar
[47]Thom, R. (1965) Sur l'homologie des variétés algebriques réelles. In Differential and Combinatorial Topology (Cairns, S. S., ed.), Princeton University Press, pp. 255–265.Google Scholar
[48]Warren, H. E. (1968) Lower bound for approximation by nonlinear manifolds. Trans. Amer. Math. Soc. 133 167–178.CrossRefGoogle Scholar
[49]Whitney, H. (1957) Elementary structure of real algebraic varieties. Ann. of Math. 66 545–556.Google Scholar
[50]Zahl, J. (2013) An improved bound on the number of point–surface incidences in three dimensions. Contrib. Discrete Math. 8 100–121.Google Scholar
[51]Zahl, J. A Szemerédi–Trotter type theorem in ℝ4. arXiv:1203.4600.Google Scholar