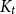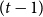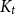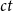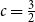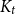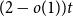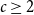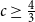1. Introduction
Preliminaries. Given a number
![]() $t \in \mathbb{N}$
, a
$t \in \mathbb{N}$
, a
![]() $K_t$
-minor is a graph
$K_t$
-minor is a graph
![]() $G$
whose vertex set can be partitioned into
$G$
whose vertex set can be partitioned into
![]() $t$
pairwise disjoint non-empty sets
$t$
pairwise disjoint non-empty sets
![]() $Z_1,\ldots,Z_t$
, such that for every
$Z_1,\ldots,Z_t$
, such that for every
![]() $i \in [t]$
, the induced subgraph
$i \in [t]$
, the induced subgraph
![]() $G[Z_i]$
is connected, and furthermore, for every two distinct
$G[Z_i]$
is connected, and furthermore, for every two distinct
![]() $i, j \in [t]$
, there exists at least one edge in
$i, j \in [t]$
, there exists at least one edge in
![]() $G$
with endpoints in the sets
$G$
with endpoints in the sets
![]() $Z_i$
and
$Z_i$
and
![]() $Z_j$
. We say that a graph contains
$Z_j$
. We say that a graph contains
![]() $K_t$
as a minor or that it contains a
$K_t$
as a minor or that it contains a
![]() $K_t$
-minor if it admits a subgraph which is a
$K_t$
-minor if it admits a subgraph which is a
![]() $K_t$
-minor.
$K_t$
-minor.
Given a graph
![]() $G$
and a colour-set
$G$
and a colour-set
![]() $S$
, a proper colouring of
$S$
, a proper colouring of
![]() $G$
with colours from
$G$
with colours from
![]() $S$
is a mapping
$S$
is a mapping
![]() $c\,{:}\,V(G) \rightarrow S$
such that
$c\,{:}\,V(G) \rightarrow S$
such that
![]() $c^{-1}(s)$
is an independent set, for every
$c^{-1}(s)$
is an independent set, for every
![]() $s \in S$
. Given a graph
$s \in S$
. Given a graph
![]() $G$
, a list assignment for
$G$
, a list assignment for
![]() $G$
is an assignment
$G$
is an assignment
![]() $L\,{:}\,V(G) \rightarrow 2^{\mathbb{N}}$
of finite sets
$L\,{:}\,V(G) \rightarrow 2^{\mathbb{N}}$
of finite sets
![]() $L(v)$
(called lists) to the vertices
$L(v)$
(called lists) to the vertices
![]() $v \in V(G)$
. An
$v \in V(G)$
. An
![]() $L$
-colouring of
$L$
-colouring of
![]() $G$
is defined as a proper colouring
$G$
is defined as a proper colouring
![]() $c\,{:}\,V(G) \rightarrow \mathbb{N}$
of
$c\,{:}\,V(G) \rightarrow \mathbb{N}$
of
![]() $G$
in which every vertex is assigned a colour from its respective list, that is,
$G$
in which every vertex is assigned a colour from its respective list, that is,
![]() $c(v) \in L(v)$
for every
$c(v) \in L(v)$
for every
![]() $v \in V(G)$
. With this, we may define the chromatic number
$v \in V(G)$
. With this, we may define the chromatic number
![]() $\chi(G)$
of a graph
$\chi(G)$
of a graph
![]() $G$
as the smallest integer
$G$
as the smallest integer
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $G$
admits an
$G$
admits an
![]() $L$
-colouring, where
$L$
-colouring, where
![]() $L(v)\,{:\!=}\,[k]$
for every
$L(v)\,{:\!=}\,[k]$
for every
![]() $v \in V(G)$
.
$v \in V(G)$
.
In a similar way, the list chromatic number
![]() $\chi _\ell(G)$
of a graph
$\chi _\ell(G)$
of a graph
![]() $G$
is defined as the smallest number
$G$
is defined as the smallest number
![]() $k \ge 1$
such that
$k \ge 1$
such that
![]() $G$
admits an
$G$
admits an
![]() $L$
-colouring for every assignment
$L$
-colouring for every assignment
![]() $L(\,{\cdot}\,)$
of colour lists to the vertices of
$L(\,{\cdot}\,)$
of colour lists to the vertices of
![]() $G$
, provided that
$G$
, provided that
![]() $|L(v)| \ge k$
for every
$|L(v)| \ge k$
for every
![]() $v \in V(G)$
.
$v \in V(G)$
.
Clearly,
![]() $\chi(G) \le \chi _\ell(G)$
for every graph
$\chi(G) \le \chi _\ell(G)$
for every graph
![]() $G$
, but in general
$G$
, but in general
![]() $\chi _\ell(G)$
is not bounded from above by a function in
$\chi _\ell(G)$
is not bounded from above by a function in
![]() $\chi(G)$
, as shown for example by complete bipartite graphs.
$\chi(G)$
, as shown for example by complete bipartite graphs.
Hadwiger’s conjecture, arguably one of the most important open problems in graph theory, states the following upper bound on the chromatic number of graphs with no
![]() $K_t$
-minor:
$K_t$
-minor:
Conjecture 1. (Hadwiger [Reference Hadwiger7], 1943) For every
![]() $t \in \mathbb{N}$
, if
$t \in \mathbb{N}$
, if
![]() $G$
is a graph not containing a
$G$
is a graph not containing a
![]() $K_t$
-minor, then
$K_t$
-minor, then
![]() $\chi(G) \le t-1$
.
$\chi(G) \le t-1$
.
Hadwiger’s conjecture and its variants have received a lot of attention in the past, and a very good overview of partial results on this topic until about
![]() $2$
years ago can be found in the survey article [Reference Seymour17] by Seymour. In the following, let us briefly highlight the milestone results regarding Hadwiger’s conjecture obtained so far.
$2$
years ago can be found in the survey article [Reference Seymour17] by Seymour. In the following, let us briefly highlight the milestone results regarding Hadwiger’s conjecture obtained so far.
As a result of Wagner [Reference Wagner22], it was known that the case
![]() $t=5$
of Hadwiger’s conjecture is equivalent to the statement of the famous four colour conjecture. After its confirmative resolution by Appel, Haken and Koch [Reference Appel and Haken1, Reference Appel, Haken and Koch2] in 1977, Hadwiger’s conjecture had been proved for all values
$t=5$
of Hadwiger’s conjecture is equivalent to the statement of the famous four colour conjecture. After its confirmative resolution by Appel, Haken and Koch [Reference Appel and Haken1, Reference Appel, Haken and Koch2] in 1977, Hadwiger’s conjecture had been proved for all values
![]() $t \le 5$
. Notably, in 1993, Robertson, Seymour and Thomas [Reference Robertson, Seymour and Thomas16] managed to go one step further and to prove Hadwiger’s conjecture also for the case
$t \le 5$
. Notably, in 1993, Robertson, Seymour and Thomas [Reference Robertson, Seymour and Thomas16] managed to go one step further and to prove Hadwiger’s conjecture also for the case
![]() $t=6$
. As of today, all the cases
$t=6$
. As of today, all the cases
![]() $t \ge 7$
of Hadwiger’s conjecture remain open problems.
$t \ge 7$
of Hadwiger’s conjecture remain open problems.
The evident difficulty of the exact version of Hadwiger’s conjecture has inspired many researchers to study its asymptotic relaxation, known as the Linear Hadwiger’s conjecture:
Conjecture 2.
There exists an absolute constant
![]() $c\gt 0$
such that every graph
$c\gt 0$
such that every graph
![]() $G$
not containing a
$G$
not containing a
![]() $K_t$
-minor satisfies
$K_t$
-minor satisfies
![]() $\chi(G) \le ct$
.
$\chi(G) \le ct$
.
While also the Linear Hadwiger’s conjecture remains open, there has been a lot of progress. By classical results of Kostochka [Reference Kostochka10] and Thomason [Reference Thomason19] from 1984, it was known that
![]() $K_t$
-minor-free graphs are
$K_t$
-minor-free graphs are
![]() $O(t\sqrt{\log t})$
-colourable. While already quite close to a linear bound, it has proven difficult to overcome this order of magnitude during more than
$O(t\sqrt{\log t})$
-colourable. While already quite close to a linear bound, it has proven difficult to overcome this order of magnitude during more than
![]() $30$
years of research. Finally, in 2019, Norine, Postle and Song [Reference Norine, Postle and Song11] managed to break this barrier, by proving that the maximum chromatic number of
$30$
years of research. Finally, in 2019, Norine, Postle and Song [Reference Norine, Postle and Song11] managed to break this barrier, by proving that the maximum chromatic number of
![]() $K_t$
-minor-free graphs is in
$K_t$
-minor-free graphs is in
![]() $O(t(\log t)^{1/4+o(1)})$
. Very soon afterwards, several related results, extensions and improvements of this bound have been obtained, see [Reference Norine and Postle12–Reference Postle15]. The current state of the art-bound of
$O(t(\log t)^{1/4+o(1)})$
. Very soon afterwards, several related results, extensions and improvements of this bound have been obtained, see [Reference Norine and Postle12–Reference Postle15]. The current state of the art-bound of
![]() $O(t \log \log t)$
has been obtained only couple of months ago by Delcourt and Postle [Reference Delcourt and Postle6].
$O(t \log \log t)$
has been obtained only couple of months ago by Delcourt and Postle [Reference Delcourt and Postle6].
Parallel to the development of Hadwiger’s conjecture, which concerns the ordinary chromatic number, the list chromatic number of graphs with no
![]() $K_t$
-minor has also received a considerable amount of interest. For example, Borowiecki [Reference Borowiecki5] asked whether every graph with no
$K_t$
-minor has also received a considerable amount of interest. For example, Borowiecki [Reference Borowiecki5] asked whether every graph with no
![]() $K_t$
-minor has list chromatic number at most
$K_t$
-minor has list chromatic number at most
![]() $t-1$
(which would strengthen Hadwiger’s conjecture). While this is easily seen to be true for
$t-1$
(which would strengthen Hadwiger’s conjecture). While this is easily seen to be true for
![]() $t \le 4$
, already for
$t \le 4$
, already for
![]() $t=5$
there exist examples of planar graphs (hence
$t=5$
there exist examples of planar graphs (hence
![]() $K_5$
-minor-free) with list chromatic number
$K_5$
-minor-free) with list chromatic number
![]() $5$
, as constructed first by Voigt [Reference Voigt21]. Later, Thomassen [Reference Thomassen20] proved that
$5$
, as constructed first by Voigt [Reference Voigt21]. Later, Thomassen [Reference Thomassen20] proved that
![]() $5$
is also the correct upper bound for the list chromatic number of planar graphs, and using Wagner’s result [Reference Wagner22], this carries over to
$5$
is also the correct upper bound for the list chromatic number of planar graphs, and using Wagner’s result [Reference Wagner22], this carries over to
![]() $K_5$
-minor-free graphs, see [Reference He, Miao and Shen8, Reference Škrekovski18]. For every
$K_5$
-minor-free graphs, see [Reference He, Miao and Shen8, Reference Škrekovski18]. For every
![]() $t \ge 6$
, the maximum list chromatic number of
$t \ge 6$
, the maximum list chromatic number of
![]() $K_t$
-minor-free graphs remains unknown.
$K_t$
-minor-free graphs remains unknown.
Since the exact version of Hadwiger’s conjecture does not extend to list colouring, it is natural to study asymptotic versions. The current state of the art-upper bound on the list chromatic number of
![]() $K_t$
-minor-free graphs is
$K_t$
-minor-free graphs is
![]() $O(t(\log \log t)^2)$
, as was recently proved by Delcourt and Postle [Reference Delcourt and Postle6]. Compare also [Reference Norine and Postle12, Reference Postle15] for the previous asymptotic upper bounds of magnitudes
$O(t(\log \log t)^2)$
, as was recently proved by Delcourt and Postle [Reference Delcourt and Postle6]. Compare also [Reference Norine and Postle12, Reference Postle15] for the previous asymptotic upper bounds of magnitudes
![]() $O(t(\log t)^{1/4+o(1)})$
and
$O(t(\log t)^{1/4+o(1)})$
and
![]() $O(t(\log \log t)^6)$
, respectively.
$O(t(\log \log t)^6)$
, respectively.
The following List Hadwiger conjecture was first stated by Kawarabayashi and Mohar [Reference Kawarabayashi and Mohar9] in 2007, compare also the entry [24] in the Open Problem Garden.
Conjecture 3.
There exists an absolute constant
![]() $c\gt 0$
such that every
$c\gt 0$
such that every
![]() $K_t$
-minor-free graph
$K_t$
-minor-free graph
![]() $G$
satisfies
$G$
satisfies
![]() $\chi _\ell(G) \le ct$
.
$\chi _\ell(G) \le ct$
.
At first, an even stronger conclusion, namely that every
![]() $K_t$
-minor-free graph is
$K_t$
-minor-free graph is
![]() $t$
-list-colourable, was believed to be possible, compare for example [Reference Kawarabayashi and Mohar9, Reference Wood23]. However, this stronger conjecture was disproved by the following result of Barát, Joret and Wood [Reference Barát, Joret and Wood3] from 2011, which shows that
$t$
-list-colourable, was believed to be possible, compare for example [Reference Kawarabayashi and Mohar9, Reference Wood23]. However, this stronger conjecture was disproved by the following result of Barát, Joret and Wood [Reference Barát, Joret and Wood3] from 2011, which shows that
![]() $c \ge \frac{4}{3}$
in Conjecture 3 is necessary.
$c \ge \frac{4}{3}$
in Conjecture 3 is necessary.
Theorem 4.
For every integer
![]() $t \ge 1$
there exists a graph with no
$t \ge 1$
there exists a graph with no
![]() $K_{3t+2}$
-minor and list chromatic number greater than
$K_{3t+2}$
-minor and list chromatic number greater than
![]() $4t$
.
$4t$
.
Kawarabayashi and Mohar stated in [Reference Kawarabayashi and Mohar9] that they believe that Conjecture 3 holds true for
![]() $c=\frac{3}{2}$
, and this statement also appears as Conjecture 8.4 in the survey article [Reference Seymour17] by Seymour:
$c=\frac{3}{2}$
, and this statement also appears as Conjecture 8.4 in the survey article [Reference Seymour17] by Seymour:
Conjecture 5.
Every graph
![]() $G$
without a
$G$
without a
![]() $K_t$
-minor satisfies
$K_t$
-minor satisfies
![]() $\chi _\ell(G) \le \frac{3}{2}t$
.
$\chi _\ell(G) \le \frac{3}{2}t$
.
In this note, we disprove Conjecture 5 by showing that the maximum list chromatic number of
![]() $K_t$
-minor-free graphs is at least
$K_t$
-minor-free graphs is at least
![]() $2t-o(t)$
, and hence
$2t-o(t)$
, and hence
![]() $c \ge 2$
in Conjecture 3 is necessary. The proof enhances an idea from [Reference Barát, Joret and Wood3] by using probabilistic arguments.
$c \ge 2$
in Conjecture 3 is necessary. The proof enhances an idea from [Reference Barát, Joret and Wood3] by using probabilistic arguments.
Theorem 6.
For every
![]() $\varepsilon \in (0,1)$
there is
$\varepsilon \in (0,1)$
there is
![]() $t_0=t_0(\varepsilon )$
such that for every
$t_0=t_0(\varepsilon )$
such that for every
![]() $t \ge t_0$
there exists a graph with no
$t \ge t_0$
there exists a graph with no
![]() $K_t$
-minor and list chromatic number at least
$K_t$
-minor and list chromatic number at least
![]() $(2-\varepsilon )t$
.
$(2-\varepsilon )t$
.
It would be interesting to see whether our lower-bound construction could be optimal up to the lower-order term, or whether further improvement of the lower bound is possible.
Problem 7.
Does every
![]() $K_t$
-minor-free graph
$K_t$
-minor-free graph
![]() $G$
satisfy
$G$
satisfy
![]() $\chi _\ell(G) \le 2t$
?
$\chi _\ell(G) \le 2t$
?
2. Proof of Theorem 6
In the following, for a natural number
![]() $n \in \mathbb{N}$
and a probability
$n \in \mathbb{N}$
and a probability
![]() $p \in [0,1]$
, we denote by
$p \in [0,1]$
, we denote by
![]() $G(n,n,p)$
the bipartite Erdős-Renyi graph, that is, a random bipartite graph
$G(n,n,p)$
the bipartite Erdős-Renyi graph, that is, a random bipartite graph
![]() $G$
with bipartition
$G$
with bipartition
![]() $A \cup B$
such that
$A \cup B$
such that
![]() $|A|=|B|=n$
, in which every pair
$|A|=|B|=n$
, in which every pair
![]() $ab$
with
$ab$
with
![]() $a \in A, b \in B$
is selected as an edge of
$a \in A, b \in B$
is selected as an edge of
![]() $G$
with probability
$G$
with probability
![]() $p$
, independently from all other such pairs.
$p$
, independently from all other such pairs.
Lemma 8.
Let
![]() $\varepsilon \in (0,1)$
be fixed, let
$\varepsilon \in (0,1)$
be fixed, let
![]() $f=f(\varepsilon ) \in \mathbb{N}$
and
$f=f(\varepsilon ) \in \mathbb{N}$
and
![]() $\delta =\delta (\varepsilon ) \in (0,1)$
be constants chosen such that
$\delta =\delta (\varepsilon ) \in (0,1)$
be constants chosen such that
![]() $f \delta \lt 1$
. Let
$f \delta \lt 1$
. Let
![]() $p=p(n)\,{:\!=}\,n^{-\delta }$
. Then w.h.p. as
$p=p(n)\,{:\!=}\,n^{-\delta }$
. Then w.h.p. as
![]() $n \rightarrow \infty$
, the random graph
$n \rightarrow \infty$
, the random graph
![]() $G=G(n,n,p(n))$
with bipartition
$G=G(n,n,p(n))$
with bipartition
![]() $A \cup B$
satisfies both of the following properties:
$A \cup B$
satisfies both of the following properties:
-
For every subset
 $X \subseteq A$
such that
$X \subseteq A$
such that
 $|X| \ge \varepsilon n$
and every collection of pairwise disjoint non-empty subsets
$|X| \ge \varepsilon n$
and every collection of pairwise disjoint non-empty subsets
 $Y_1,\ldots,Y_k \subseteq B$
such that
$Y_1,\ldots,Y_k \subseteq B$
such that
 $k \ge \varepsilon n$
and
$k \ge \varepsilon n$
and
 $\max \{|Y_1|,\ldots,|Y_k|\} \le f$
, there exists a vertex
$\max \{|Y_1|,\ldots,|Y_k|\} \le f$
, there exists a vertex
 $x \in X$
and some
$x \in X$
and some
 $j \in [k]$
such that
$j \in [k]$
such that
 $G$
contains all the edges
$G$
contains all the edges
 $xy, y \in Y_j$
. The same statement holds symmetrically for the case when
$xy, y \in Y_j$
. The same statement holds symmetrically for the case when
 $X \subseteq B$
and
$X \subseteq B$
and
 $Y_1,\ldots,Y_k \subseteq A$
.
$Y_1,\ldots,Y_k \subseteq A$
. -
 $G$
has maximum degree at most
$G$
has maximum degree at most
 $\varepsilon n$
.
$\varepsilon n$
.
Proof.
-
Let
 $E_n$
denote the probability event that
$E_n$
denote the probability event that
 $G$
does not satisfy the property claimed in the first item. We need to show that
$G$
does not satisfy the property claimed in the first item. We need to show that
 $\mathbb{P}(E_n) \rightarrow 0$
as
$\mathbb{P}(E_n) \rightarrow 0$
as
 $n \rightarrow \infty$
. So consider a fixed subset
$n \rightarrow \infty$
. So consider a fixed subset
 $X \subseteq A$
(or symmetrically,
$X \subseteq A$
(or symmetrically,
 $X \subseteq B$
) such that
$X \subseteq B$
) such that
 $|X| \ge \varepsilon n$
, and a fixed collection
$|X| \ge \varepsilon n$
, and a fixed collection
 $Y_1,\ldots,Y_k$
of disjoint non-empty subsets of
$Y_1,\ldots,Y_k$
of disjoint non-empty subsets of
 $B$
(or symmetrically,
$B$
(or symmetrically,
 $A$
), where
$A$
), where
 $k \ge \varepsilon n$
and
$k \ge \varepsilon n$
and
 $\max \{|Y_1|,\ldots,|Y_k|\} \le f$
. Let
$\max \{|Y_1|,\ldots,|Y_k|\} \le f$
. Let
 $E(X,Y_1,\ldots,Y_k)$
be the probability event ‘there exists no pair
$E(X,Y_1,\ldots,Y_k)$
be the probability event ‘there exists no pair
 $(x,j) \in X \times [k]$
such that
$(x,j) \in X \times [k]$
such that
 $x$
is fully connected to the vertices in
$x$
is fully connected to the vertices in
 $Y_j$
’. Fixing a vertex
$Y_j$
’. Fixing a vertex
 $x \in X$
and an index
$x \in X$
and an index
 $j \in [k]$
, clearly the probability of the event that ‘
$j \in [k]$
, clearly the probability of the event that ‘
 $x$
is not fully connected to
$x$
is not fully connected to
 $Y_j$
’ equals
$Y_j$
’ equals
 $1-p^{|Y_j|} \le 1-p^{f}$
. Since these events are independent for different choices of
$1-p^{|Y_j|} \le 1-p^{f}$
. Since these events are independent for different choices of
 $(x,j)$
, we conclude that
With a rough estimate, there are at most
$(x,j)$
, we conclude that
With a rough estimate, there are at most \begin{equation*}\mathbb {P}(E(X,Y_1,\ldots,Y_k)) \le \big(1-p^{f}\big)^{|X|\cdot k} \le \big(1-p^{f}\big)^{\varepsilon ^2n^2}\le \exp\!(\!-p^{f}\varepsilon ^2 n^2)=\exp\!\left(\!-\varepsilon ^2n^{2-f\delta }\right).\end{equation*}
ways to select the sets
\begin{equation*}\mathbb {P}(E(X,Y_1,\ldots,Y_k)) \le \big(1-p^{f}\big)^{|X|\cdot k} \le \big(1-p^{f}\big)^{\varepsilon ^2n^2}\le \exp\!(\!-p^{f}\varepsilon ^2 n^2)=\exp\!\left(\!-\varepsilon ^2n^{2-f\delta }\right).\end{equation*}
ways to select the sets \begin{equation*}2 \cdot 2^n\cdot (n+1)^{n} = \exp\!(\!\ln\!(2)(n+1)+n \ln\!(n+1))\end{equation*}
\begin{equation*}2 \cdot 2^n\cdot (n+1)^{n} = \exp\!(\!\ln\!(2)(n+1)+n \ln\!(n+1))\end{equation*}
 $X,Y_1,\ldots,Y_k$
. Hence, applying a union bound we find that
The right hand side of the above inequality tends to
$X,Y_1,\ldots,Y_k$
. Hence, applying a union bound we find that
The right hand side of the above inequality tends to \begin{equation*}\mathbb {P}(E_n) \le \exp\!(\!\ln\!(2)(n+1)+n \ln\!(n+1)-\varepsilon ^2n^{2-f\delta }).\end{equation*}
\begin{equation*}\mathbb {P}(E_n) \le \exp\!(\!\ln\!(2)(n+1)+n \ln\!(n+1)-\varepsilon ^2n^{2-f\delta }).\end{equation*}
 $0$
as
$0$
as
 $n \rightarrow \infty$
, since
$n \rightarrow \infty$
, since
 $f\delta \lt 1$
and hence
$f\delta \lt 1$
and hence
 $\varepsilon ^2n^{2-f\delta }=\Omega (n^{2-f\delta })$
grows faster than
$\varepsilon ^2n^{2-f\delta }=\Omega (n^{2-f\delta })$
grows faster than
 $\ln\!(2)(n+1)+n \ln\!(n+1)=O(n\ln n)$
. This proves that
$\ln\!(2)(n+1)+n \ln\!(n+1)=O(n\ln n)$
. This proves that
 $G$
satisfies the properties claimed by the first item w.h.p., as required.
$G$
satisfies the properties claimed by the first item w.h.p., as required.
-
To show that also the property claimed by the second item holds true w.h.p., consider the probability that a fixed vertex
 $x \in A \cup B$
has more than
$x \in A \cup B$
has more than
 $\varepsilon n$
neighbours in
$\varepsilon n$
neighbours in
 $G$
. Note that the degree of
$G$
. Note that the degree of
 $x$
in
$x$
in
 $G(n,n,p)$
is distributed like a binomial random variable
$G(n,n,p)$
is distributed like a binomial random variable
 $B(n,p)$
, and hence its expectancy is
$B(n,p)$
, and hence its expectancy is
 $np=n^{1-\delta }$
, which is smaller than
$np=n^{1-\delta }$
, which is smaller than
 $\frac{\varepsilon n}{2}$
for
$\frac{\varepsilon n}{2}$
for
 $n$
sufficiently large in terms of
$n$
sufficiently large in terms of
 $\varepsilon$
and
$\varepsilon$
and
 $\delta$
. Applying Chernoff’s bound we find for every sufficiently large
$\delta$
. Applying Chernoff’s bound we find for every sufficiently large
 $n$
:
Since this bound applies to every choice of
$n$
:
Since this bound applies to every choice of \begin{equation*}\mathbb {P}(d_G(x)\gt \varepsilon n )\le \mathbb {P}(B(n,p)\gt 2np) \le \exp\!\left (-\frac {1}{3}np\right )=\exp\!\left (-\frac {1}{3}n^{1-\delta }\right ).\end{equation*}
\begin{equation*}\mathbb {P}(d_G(x)\gt \varepsilon n )\le \mathbb {P}(B(n,p)\gt 2np) \le \exp\!\left (-\frac {1}{3}np\right )=\exp\!\left (-\frac {1}{3}n^{1-\delta }\right ).\end{equation*}
 $x \in A \cup B$
, applying a union bound we find that the probability that
$x \in A \cup B$
, applying a union bound we find that the probability that
 $G$
has maximum degree more than
$G$
has maximum degree more than
 $\varepsilon n$
is at most
which tends to
$\varepsilon n$
is at most
which tends to \begin{equation*}2n\exp\!\left (-\frac {1}{3}n^{1-\delta }\right )=\exp\!\left (\ln\!(2n)-\frac {1}{3}n^{1-\delta }\right )\end{equation*}
\begin{equation*}2n\exp\!\left (-\frac {1}{3}n^{1-\delta }\right )=\exp\!\left (\ln\!(2n)-\frac {1}{3}n^{1-\delta }\right )\end{equation*}
 $0$
as
$0$
as
 $n \rightarrow \infty$
, as desired (here we used that
$n \rightarrow \infty$
, as desired (here we used that
 $\delta \lt 1$
and hence
$\delta \lt 1$
and hence
 $n^{1-\delta }$
grows faster than
$n^{1-\delta }$
grows faster than
 $\ln\!(2n)$
).
$\ln\!(2n)$
).
The next lemma uses Lemma 8 to obtain a useful deterministic statement about the existence of graphs with certain properties, which are then handy when constructing the lower-bound examples for Theorem 6.
Lemma 9.
For every
![]() $\varepsilon \in (0,1)$
, there is
$\varepsilon \in (0,1)$
, there is
![]() $n_0=n_0(\varepsilon )$
such that for every
$n_0=n_0(\varepsilon )$
such that for every
![]() $n \ge n_0$
, there exists a graph
$n \ge n_0$
, there exists a graph
![]() $H$
whose vertex set
$H$
whose vertex set
![]() $V(H)=A \cup B$
is partitioned into two disjoint sets
$V(H)=A \cup B$
is partitioned into two disjoint sets
![]() $A$
and
$A$
and
![]() $B$
of size
$B$
of size
![]() $n$
, and such that the following properties hold:
$n$
, and such that the following properties hold:
-
Both
 $A$
and
$A$
and
 $B$
are cliques of
$B$
are cliques of
 $H$
,
$H$
, -
every vertex in
 $H$
has at most
$H$
has at most
 $\varepsilon n$
non-neighbours in
$\varepsilon n$
non-neighbours in
 $H$
, and
$H$
, and
-
for every
 $t \in \mathbb{N}$
such that
$t \in \mathbb{N}$
such that
 $t \ge (1+2\varepsilon ) n$
,
$t \ge (1+2\varepsilon ) n$
,
 $H$
does not contain
$H$
does not contain
 $K_t$
as a minor.
$K_t$
as a minor.
Proof. Let
![]() $f\,{:\!=}\,\lceil \frac{1}{\varepsilon } \rceil \in \mathbb{N}$
and
$f\,{:\!=}\,\lceil \frac{1}{\varepsilon } \rceil \in \mathbb{N}$
and
![]() $\delta \,{:\!=}\,\frac{\varepsilon }{2}$
. Then
$\delta \,{:\!=}\,\frac{\varepsilon }{2}$
. Then
![]() $f\delta \lt 1$
, and hence we may apply Lemma 8. It follows directly that there exists
$f\delta \lt 1$
, and hence we may apply Lemma 8. It follows directly that there exists
![]() $n_0=n_0(\varepsilon ) \in \mathbb{N}$
such that for every
$n_0=n_0(\varepsilon ) \in \mathbb{N}$
such that for every
![]() $n \ge n_0$
there exists a bipartite graph
$n \ge n_0$
there exists a bipartite graph
![]() $G$
, whose bipartition classes
$G$
, whose bipartition classes
![]() $A$
and
$A$
and
![]() $B$
are both of size
$B$
are both of size
![]() $n$
, and such that
$n$
, and such that
-
For every subset
 $X \subseteq A$
such that
$X \subseteq A$
such that
 $|X| \ge \varepsilon n$
and every collection of pairwise disjoint non-empty subsets
$|X| \ge \varepsilon n$
and every collection of pairwise disjoint non-empty subsets
 $Y_1,\ldots,Y_k \subseteq B$
such that
$Y_1,\ldots,Y_k \subseteq B$
such that
 $k \ge \varepsilon n$
and
$k \ge \varepsilon n$
and
 $\max \{|Y_1|,\ldots,|Y_k|\} \le f$
, there exists a vertex
$\max \{|Y_1|,\ldots,|Y_k|\} \le f$
, there exists a vertex
 $x \in X$
and some
$x \in X$
and some
 $j \in [k]$
such that
$j \in [k]$
such that
 $G$
contains all the edges
$G$
contains all the edges
 $xy, y \in Y_j$
. The same statement holds symmetrically for the case when
$xy, y \in Y_j$
. The same statement holds symmetrically for the case when
 $X \subseteq B$
and
$X \subseteq B$
and
 $Y_1,\ldots,Y_k \subseteq A$
.
$Y_1,\ldots,Y_k \subseteq A$
. -
 $G$
has maximum degree at most
$G$
has maximum degree at most
 $\varepsilon n$
.
$\varepsilon n$
.
We now define
![]() $H$
as the complement of
$H$
as the complement of
![]() $G$
(also with vertex set
$G$
(also with vertex set
![]() $A \cup B$
). Since
$A \cup B$
). Since
![]() $G$
is bipartite, clearly
$G$
is bipartite, clearly
![]() $A$
and
$A$
and
![]() $B$
form cliques in
$B$
form cliques in
![]() $H$
, verifying the first item. The second item follows directly from the fact that
$H$
, verifying the first item. The second item follows directly from the fact that
![]() $\Delta(G) \le \varepsilon n$
.
$\Delta(G) \le \varepsilon n$
.
It hence remains to verify the last item. Towards a contradiction, suppose that there exists a number
![]() $t \in \mathbb{N}$
,
$t \in \mathbb{N}$
,
![]() $t \ge (1+2\varepsilon )n$
, such that
$t \ge (1+2\varepsilon )n$
, such that
![]() $H$
contains
$H$
contains
![]() $K_t$
as a minor. This implies that there exists a collection
$K_t$
as a minor. This implies that there exists a collection
![]() $\mathcal{Z}$
of non-empty and pairwise disjoint subsets of
$\mathcal{Z}$
of non-empty and pairwise disjoint subsets of
![]() $V(H)$
such that
$V(H)$
such that
![]() $|\mathcal{Z}|=t$
and such that for every two distinct
$|\mathcal{Z}|=t$
and such that for every two distinct
![]() $Z, Z' \in \mathcal{Z}$
, there exists at least one edge in
$Z, Z' \in \mathcal{Z}$
, there exists at least one edge in
![]() $H$
connecting a vertex in
$H$
connecting a vertex in
![]() $Z$
to a vertex in
$Z$
to a vertex in
![]() $Z'$
. Let us denote
$Z'$
. Let us denote
![]() $\mathcal{Z}_s\,{:\!=}\,\{Z \in \mathcal{Z}||Z|=s\}$
, and
$\mathcal{Z}_s\,{:\!=}\,\{Z \in \mathcal{Z}||Z|=s\}$
, and
![]() $z_s\,{:\!=}\,|\mathcal{Z}_s|$
, for every
$z_s\,{:\!=}\,|\mathcal{Z}_s|$
, for every
![]() $s \ge 1$
. We clearly have
$s \ge 1$
. We clearly have
Rearranging yields that
![]() $z_1 \ge 4\varepsilon n$
. From this, we may conclude that either
$z_1 \ge 4\varepsilon n$
. From this, we may conclude that either
![]() $A$
or
$A$
or
![]() $B$
contains at least
$B$
contains at least
![]() $2 \varepsilon n$
singletons from
$2 \varepsilon n$
singletons from
![]() $\mathcal{Z}$
. By symmetry (possibly by renaming
$\mathcal{Z}$
. By symmetry (possibly by renaming
![]() $A$
and
$A$
and
![]() $B$
), we may assume w.l.o.g. that
$B$
), we may assume w.l.o.g. that
![]() $B$
contains at least
$B$
contains at least
![]() $2 \varepsilon n$
singletons from
$2 \varepsilon n$
singletons from
![]() $\mathcal{Z}$
, and denote the set of these singletons by
$\mathcal{Z}$
, and denote the set of these singletons by
![]() $X$
. Let us now define
$X$
. Let us now define
![]() $\mathcal{Z}_A\,{:\!=}\,\{Z \in \mathcal{Z}|Z \subseteq A\}$
and
$\mathcal{Z}_A\,{:\!=}\,\{Z \in \mathcal{Z}|Z \subseteq A\}$
and
![]() $\mathcal{Z}_B\,{:\!=}\,\{Z \in \mathcal{Z}|Z \cap B \neq \emptyset \}$
. Since the sets in
$\mathcal{Z}_B\,{:\!=}\,\{Z \in \mathcal{Z}|Z \cap B \neq \emptyset \}$
. Since the sets in
![]() $\mathcal{Z}$
are pairwise disjoint, we can see that
$\mathcal{Z}$
are pairwise disjoint, we can see that
![]() $|\mathcal{Z}_B| \le |B|=n$
, and therefore
$|\mathcal{Z}_B| \le |B|=n$
, and therefore
![]() $|\mathcal{Z}_A|=t-|\mathcal{Z}_B| \ge t-n \ge 2\varepsilon n$
. Since
$|\mathcal{Z}_A|=t-|\mathcal{Z}_B| \ge t-n \ge 2\varepsilon n$
. Since
![]() $|A|=n$
, the latter implies that there are at least
$|A|=n$
, the latter implies that there are at least
![]() $\varepsilon n$
distinct sets in
$\varepsilon n$
distinct sets in
![]() $\mathcal{Z}_A$
which have size at most
$\mathcal{Z}_A$
which have size at most
![]() $\frac{1}{\varepsilon }$
. Let
$\frac{1}{\varepsilon }$
. Let
![]() $Y_1,\ldots,Y_k$
with
$Y_1,\ldots,Y_k$
with
![]() $k \ge \varepsilon n$
be an enumeration of the sets in
$k \ge \varepsilon n$
be an enumeration of the sets in
![]() $\mathcal{Z}_A$
of size at most
$\mathcal{Z}_A$
of size at most
![]() $\frac{1}{\varepsilon } \le f$
. By the above, there exists
$\frac{1}{\varepsilon } \le f$
. By the above, there exists
![]() $j \in [k]$
and a vertex
$j \in [k]$
and a vertex
![]() $x \in X$
such that
$x \in X$
such that
![]() $xy \in E(G)$
for every
$xy \in E(G)$
for every
![]() $y \in Y_j$
. Since
$y \in Y_j$
. Since
![]() $H$
is the complement of
$H$
is the complement of
![]() $G$
, this means that
$G$
, this means that
![]() $\{x\}$
and
$\{x\}$
and
![]() $Y_j$
are distinct sets in
$Y_j$
are distinct sets in
![]() $\mathcal{Z}$
, which do not have any connecting edge. This is a contradiction to our initial assumptions, and hence we have shown that the third item claimed in the lemma is also satisfied. This concludes the proof.
$\mathcal{Z}$
, which do not have any connecting edge. This is a contradiction to our initial assumptions, and hence we have shown that the third item claimed in the lemma is also satisfied. This concludes the proof.
We are now ready for the proof of Theorem 6. The only missing ingredient is the following well-known ‘pasting-lemma’, compare Lemma 3 in [Reference Barát, Joret and Wood3].
Lemma 10.
Let
![]() $G_1$
and
$G_1$
and
![]() $G_2$
be -minor-free graphs, and let
$G_2$
be -minor-free graphs, and let
![]() $V(G_1) \cap V(G_2)=C$
. If
$V(G_1) \cap V(G_2)=C$
. If
![]() $C$
forms a clique in both
$C$
forms a clique in both
![]() $G_1$
and
$G_1$
and
![]() $G_2$
, then the graph
$G_2$
, then the graph
![]() $G_1 \cup G_2$
is also
$G_1 \cup G_2$
is also
![]() $K_t$
-minor-free.
$K_t$
-minor-free.
Proof of Theorem 6. Let a fixed
![]() $\varepsilon \in (0,1)$
be given. Pick some
$\varepsilon \in (0,1)$
be given. Pick some
![]() $\varepsilon ' \in (0,1)$
such that
$\varepsilon ' \in (0,1)$
such that
![]() $\frac{2-\varepsilon '}{1+2\varepsilon '} \ge 2-\frac{\varepsilon }{2}$
. Let
$\frac{2-\varepsilon '}{1+2\varepsilon '} \ge 2-\frac{\varepsilon }{2}$
. Let
![]() $n_0=n_0(\varepsilon ') \in \mathbb{N}$
be as in Lemma 9, and define
$n_0=n_0(\varepsilon ') \in \mathbb{N}$
be as in Lemma 9, and define
![]() $t_0\,{:\!=}\,\max \{\lceil (1+2\varepsilon ')n_0\rceil,\left \lceil \frac{4}{\varepsilon }\right \rceil \}$
. Now, let
$t_0\,{:\!=}\,\max \{\lceil (1+2\varepsilon ')n_0\rceil,\left \lceil \frac{4}{\varepsilon }\right \rceil \}$
. Now, let
![]() $t \ge t_0$
be any given integer. Define
$t \ge t_0$
be any given integer. Define
![]() $n\,{:\!=}\,\left \lfloor \frac{t}{1+2\varepsilon '}\right \rfloor \ge n_0$
. Applying Lemma 9, we find that there exists a graph
$n\,{:\!=}\,\left \lfloor \frac{t}{1+2\varepsilon '}\right \rfloor \ge n_0$
. Applying Lemma 9, we find that there exists a graph
![]() $H$
whose vertex set is partitioned into two non-empty sets
$H$
whose vertex set is partitioned into two non-empty sets
![]() $A$
and
$A$
and
![]() $B$
of size
$B$
of size
![]() $n$
, such that both
$n$
, such that both
![]() $A$
and
$A$
and
![]() $B$
form cliques in
$B$
form cliques in
![]() $H$
, every vertex in
$H$
, every vertex in
![]() $H$
has at most
$H$
has at most
![]() $\varepsilon ' n$
non-neighbours, and
$\varepsilon ' n$
non-neighbours, and
![]() $H$
is
$H$
is
![]() $K_t$
-minor-free (since
$K_t$
-minor-free (since
![]() $t \ge (1+2\varepsilon ')n$
, by definition of
$t \ge (1+2\varepsilon ')n$
, by definition of
![]() $n$
).
$n$
).
For every possible assignment
![]() $c \in [2n-1]^A$
of colours from
$c \in [2n-1]^A$
of colours from
![]() $[2n-1]$
to vertices in
$[2n-1]$
to vertices in
![]() $A$
, denote by
$A$
, denote by
![]() $H(c)$
an isomorphic copy of
$H(c)$
an isomorphic copy of
![]() $H$
, such that the vertex set of
$H$
, such that the vertex set of
![]() $H(c)$
decomposes into the sets
$H(c)$
decomposes into the sets
![]() $A$
and
$A$
and
![]() $B(c)$
of size
$B(c)$
of size
![]() $n$
. More precisely, the distinct copies
$n$
. More precisely, the distinct copies
![]() $H(c), c \in [2n-1]^A$
of
$H(c), c \in [2n-1]^A$
of
![]() $H$
share the same set
$H$
share the same set
![]() $A$
but have pairwise disjoint sets
$A$
but have pairwise disjoint sets
![]() $B(c)$
. Since
$B(c)$
. Since
![]() $A$
forms a clique of size
$A$
forms a clique of size
![]() $n$
in the
$n$
in the
![]() $K_t$
-minor-free graph
$K_t$
-minor-free graph
![]() $H(c)$
for every colouring
$H(c)$
for every colouring
![]() $c\,{:}\,A \rightarrow [2n-1]$
, it follows by repeated application of Lemma 10 that the graph
$c\,{:}\,A \rightarrow [2n-1]$
, it follows by repeated application of Lemma 10 that the graph
![]() $\mathbf{G}$
with vertex set
$\mathbf{G}$
with vertex set
![]() $A \cup \bigcup _{c \in [2n-1]^A}{B(c)}$
, obtained as the union of the graphs
$A \cup \bigcup _{c \in [2n-1]^A}{B(c)}$
, obtained as the union of the graphs
![]() $H(c), c \in [2n-1]^A$
, is
$H(c), c \in [2n-1]^A$
, is
![]() $K_t$
-minor-free.
$K_t$
-minor-free.
Now, consider an assignment
![]() $L\,{:}\,V(\mathbf{G}) \rightarrow 2^{\mathbb{N}}$
of colour lists to the vertices of
$L\,{:}\,V(\mathbf{G}) \rightarrow 2^{\mathbb{N}}$
of colour lists to the vertices of
![]() $\mathbf{G}$
as follows: For every vertex
$\mathbf{G}$
as follows: For every vertex
![]() $a \in A$
, we define
$a \in A$
, we define
![]() $L(a)\,{:\!=}\,[2n-1]$
, and for every vertex
$L(a)\,{:\!=}\,[2n-1]$
, and for every vertex
![]() $b \in B(c)$
for some colouring
$b \in B(c)$
for some colouring
![]() $c \in [2n-1]^A$
of
$c \in [2n-1]^A$
of
![]() $A$
, we define
$A$
, we define
![]() $L(b)\,{:\!=}\, [2n-1] \setminus \{c(a)|a \in A, ab \notin E(H(c))\}$
. Note that since every vertex in
$L(b)\,{:\!=}\, [2n-1] \setminus \{c(a)|a \in A, ab \notin E(H(c))\}$
. Note that since every vertex in
![]() $B(c)$
has at most
$B(c)$
has at most
![]() $\varepsilon ' n$
non-neighbours in
$\varepsilon ' n$
non-neighbours in
![]() $H(c)$
, we have
$H(c)$
, we have
![]() $|L(v)| \ge 2n-1-\varepsilon ' n$
for every vertex
$|L(v)| \ge 2n-1-\varepsilon ' n$
for every vertex
![]() $v \in V(\mathbf{G})$
.
$v \in V(\mathbf{G})$
.
We now claim that
![]() $\mathbf{G}$
does not admit a proper colouring with colours chosen from the lists
$\mathbf{G}$
does not admit a proper colouring with colours chosen from the lists
![]() $L(v), v \in V(\mathbf{G})$
, which will then prove that
$L(v), v \in V(\mathbf{G})$
, which will then prove that
![]() $\chi _\ell (\mathbf{G}) \ge 2n-\varepsilon ' n$
. Indeed, suppose towards a contradiction there exists a proper colouring
$\chi _\ell (\mathbf{G}) \ge 2n-\varepsilon ' n$
. Indeed, suppose towards a contradiction there exists a proper colouring
![]() $c_{\mathbf{G}}\,{:}\,V(\mathbf{G}) \rightarrow \mathbb{N}$
of
$c_{\mathbf{G}}\,{:}\,V(\mathbf{G}) \rightarrow \mathbb{N}$
of
![]() $\mathbf{G}$
such that
$\mathbf{G}$
such that
![]() $c_{\mathbf{G}}(v) \in L(v)$
for every
$c_{\mathbf{G}}(v) \in L(v)$
for every
![]() $v \in V(\mathbf{G})$
. Let
$v \in V(\mathbf{G})$
. Let
![]() $c$
be the restriction of
$c$
be the restriction of
![]() $c_{\mathbf{G}}$
to
$c_{\mathbf{G}}$
to
![]() $A$
, and consider the proper colouring of
$A$
, and consider the proper colouring of
![]() $H(c)$
obtained by restricting
$H(c)$
obtained by restricting
![]() $c_{\mathbf{G}}$
. Since
$c_{\mathbf{G}}$
. Since
![]() $H(c)$
has order
$H(c)$
has order
![]() $2n$
and
$2n$
and
![]() $c_{\mathbf{G}}(v) \in [2n-1]$
for every
$c_{\mathbf{G}}(v) \in [2n-1]$
for every
![]() $v \in V(H(c))$
, there must exist two (necessarily non-adjacent) vertices in
$v \in V(H(c))$
, there must exist two (necessarily non-adjacent) vertices in
![]() $H(c)$
which have the same colour with respect to
$H(c)$
which have the same colour with respect to
![]() $c_{\mathbf{G}}$
. Concretely, there exist
$c_{\mathbf{G}}$
. Concretely, there exist
![]() $a \in A$
,
$a \in A$
,
![]() $b\in B(c)$
such that
$b\in B(c)$
such that
![]() $ab \notin E(H(c))$
and
$ab \notin E(H(c))$
and
![]() $c_{\mathbf{G}}(a)=c_{\mathbf{G}}(b)$
. This however yields a contradiction, since
$c_{\mathbf{G}}(a)=c_{\mathbf{G}}(b)$
. This however yields a contradiction, since
![]() $c_{\mathbf{G}}(b) \in L(b)$
and by definition
$c_{\mathbf{G}}(b) \in L(b)$
and by definition
![]() $c(a)=c_{\mathbf{G}}(a)$
is not included in the list of
$c(a)=c_{\mathbf{G}}(a)$
is not included in the list of
![]() $b$
.
$b$
.
We conclude that indeed,
![]() $\mathbf{G}$
is a
$\mathbf{G}$
is a
![]() $K_t$
-minor-free graph which satisfies
$K_t$
-minor-free graph which satisfies
 \begin{align*}\chi _\ell (\mathbf {G}) \ge (2-\varepsilon ')n&=(2-\varepsilon ')\left \lfloor \frac {t}{1+2\varepsilon '}\right \rfloor \gt (2-\varepsilon ')\left (\frac {t}{1+2\varepsilon '}-1\right )\\[3pt] &\ge \left (2-\frac {\varepsilon }{2}\right )t-(2-\varepsilon ') \ge (2-\varepsilon )t,\end{align*}
\begin{align*}\chi _\ell (\mathbf {G}) \ge (2-\varepsilon ')n&=(2-\varepsilon ')\left \lfloor \frac {t}{1+2\varepsilon '}\right \rfloor \gt (2-\varepsilon ')\left (\frac {t}{1+2\varepsilon '}-1\right )\\[3pt] &\ge \left (2-\frac {\varepsilon }{2}\right )t-(2-\varepsilon ') \ge (2-\varepsilon )t,\end{align*}
where for the last inequality we used
![]() $t \ge t_0 \ge \frac{4}{\varepsilon }$
.
$t \ge t_0 \ge \frac{4}{\varepsilon }$
.