Article contents
Largest Components in Random Hypergraphs
Published online by Cambridge University Press: 04 April 2018
Abstract
In this paper we consider j-tuple-connected components in random k-uniform hypergraphs (the j-tuple-connectedness relation can be defined by letting two j-sets be connected if they lie in a common edge and considering the transitive closure; the case j = 1 corresponds to the common notion of vertex-connectedness). We show that the existence of a j-tuple-connected component containing Θ(nj) j-sets undergoes a phase transition and show that the threshold occurs at edge probability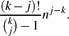 $$\frac{(k-j)!}{\binom{k}{j}-1}n^{j-k}.$$
$$\frac{(k-j)!}{\binom{k}{j}-1}n^{j-k}.$$
Our main original contribution is a bounded degree lemma, which controls the structure of the component grown in the search process.
Keywords
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2018
Footnotes
The first and third authors were supported by short visit grants 5639 and 5472, respectively, from the European Science Foundation (ESF) within the ‘Random Geometry of Large Interacting Systems and Statistical Physics’ (RGLIS) programme.
The second author is supported by Austrian Science Fund (FWF): P26826, W1230, Doctoral Programme ‘Discrete Mathematics’.
References
- 9
- Cited by

