Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-25T13:51:35.169Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Limit Theorems for the Giant Component of Random Hypergraphs†

Published online by Cambridge University Press:  13 February 2014

MICHAEL BEHRISCH ,
AMIN COJA-OGHLAN  and
MIHYUN KANG
MICHAEL BEHRISCH
Affiliation:
Institute of Transportation Systems, German Aerospace Center, Rutherfordstrasse 2, 12489 Berlin, Germany (e-mail: michael.behrisch@dlr.de)
AMIN COJA-OGHLAN
Affiliation:
Goethe University, Mathematics Institute, 60054 Frankfurt am Main, Germany (e-mail: acoghlan@math.uni-frankfurt.de)
MIHYUN KANG
Affiliation:
TU Graz, Institut für Optimierung und Diskrete Mathematik (Math B), Steyrergasse 30, 8010 Graz, Austria (e-mail: kang@math.tugraz.at)
Get access Rights & Permissions [Opens in a new window]

Abstract

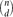Let Hd(n,p) signify a random d-uniform hypergraph with n vertices in which each of the $\binom{n}{d}$ possible edges is present with probability p=p(n) independently, and let Hd(n,m) denote a uniformly distributed d-uniform hypergraph with n vertices and m edges. We derive local limit theorems for the joint distribution of the number of vertices and the number of edges in the largest component of Hd(n,p) and Hd(n,m) in the regime 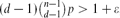$(d-1)\binom{n-1}{d-1}p>1+\varepsilon$, resp. d(d−1)m/n>1+ϵ, where ϵ>0 is arbitrarily small but fixed as n → ∞. The proofs are based on a purely probabilistic approach.

Keywords

Primary 05C80Secondary 05C65
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 3 , May 2014 , pp. 331 - 366
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

An extended abstract version of this work appeared in the proceedings of RANDOM 2007, Vol. 4627 of Lecture Notes in Computer Science, Springer, pp. 341–352.

References

[1]Alon, N. and Spencer, J. (2000) The Probabilistic Method, second edition, Wiley.Google Scholar
[2]Andriamampianina, T. and Ravelomanana, V. (2005) Enumeration of connected uniform hypergraphs. In Proc. FPSAC 2005.Google Scholar
[3]Barbour, A. D., Karoński, M. and Ruciński, A. (1989) A central limit theorem for decomposable random variables with applications to random graphs. J. Combin. Theory Ser. B 47 125–145.Google Scholar
[4]Barraez, D., Boucheron, S. and Fernandez de la Vega, W. (2000) On the fluctuations of the giant component. Combin. Probab. Comput. 9 287–304.Google Scholar
[5]Behrisch, M. (2007) Stochastical models for networks in the life sciences. PhD thesis, Humboldt Universität zu Berlin.Google Scholar
[6]Behrisch, M., Coja-Oghlan, A. and Kang, M. (2010) The order of the giant component of random hypergraphs. Random Struct. Alg. 36 149–184.Google Scholar
[7]Behrisch, M., Coja-Oghlan, A. and Kang, M. (2014) The asymptotic probability that a random d-uniform hypergraph is connected. Combin. Probab. Comput. doi:10.1017/S0963548314000029.Google Scholar
[8]Bender, E. A., Canfield, E. R. and McKay, B. D. (1990) The asymptotic number of labeled connected graphs with a given number of vertices and edges. Random Struct. Alg. 1 127–169.Google Scholar
[9]Bender, E. A., Canfield, E. R. and McKay, B. D. (1992) Asymptotic properties of labeled connected graphs. Random Struct. Alg. 3 183–202.Google Scholar
[10]Bollobás, B. (2001) Random Graphs, second edition, Cambridge University Press.CrossRefGoogle Scholar
[11]Bollobás, B. and Riordan, O. (2012) Asymptotic normality of the size of the giant component via a random walk. J. Combin. Theory Ser. B 102 53–61.Google Scholar
[12]Bollobás, B. and Riordan, O. (2012) Asymptotic normality of the size of the giant component in a random hypergraph. Random Struct. Alg. 41 441–450.Google Scholar
[13]Coja-Oghlan, A., Moore, C. and Sanwalani, V. (2007) Counting connected graphs and hypergraphs via the probabilistic method. Random Struct. Alg. 31 288–329.Google Scholar
[14]Coppersmith, D., Gamarnik, D., Hajiaghayi, M. and Sorkin, G. B. (2004) Random MAX SAT, random MAX CUT, and their phase transitions. Random Struct. Alg. 24 502–545.Google Scholar
[15]Erdős, P. and Rényi, A. (1959) On random graphs I. Publicationes Math. Debrecen 5 290–297.Google Scholar
[16]Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Publ. Math. Inst. Hungar. Acad. Sci. 5 17–61.Google Scholar
[17]van der Hofstad, R. and Spencer, J. (2006) Counting connected graphs asymptotically. European J. Combin. 27 1294–1320.Google Scholar
[18]Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.Google Scholar
[19]Karoński, M. and Łuczak, T. (1997) The number of connected sparsely edged uniform hypergraphs. Discrete Math. 171 153–168.Google Scholar
[20]Karoński, M. and Łuczak, T. (2002) The phase transition in a random hypergraph. J. Comput. Appl. Math. 142 125–135.Google Scholar
[21]Łuczak, T. (1990) On the number of sparse connected graphs. Random Struct. Alg. 1 171–173.Google Scholar
[22]O'Connell, N. (1998) Some large deviation results for sparse random graphs. Probab. Theory Rel. Fields 110 277–285.Google Scholar
[23]Pittel, B. (1990) On tree census and the giant component in sparse random graphs. Random Struct. Alg. 1 311–342.Google Scholar
[24]Pittel, B. and Wormald, N. C. (2003) Asymptotic enumeration of sparse graphs with a minimum degree constraint. J. Combin. Theory Ser. A 101 249–263.Google Scholar
[25]Pittel, B. and Wormald, N. C. (2005) Counting connected graphs inside out. J. Combin. Theory Ser. B 93 127–172.Google Scholar
[26]Ravelomanana, V. and Rijamamy, A. L. (2006) Creation and growth of components in a random hypergraph process. In Computing and Combinatorics, Vol. 4112 of Lecture Notes in Computer Science, Springer, pp. 350–359.CrossRefGoogle Scholar
[27]Rudin, W. (1987) Real and Complex Analysis, third edition, McGraw-Hill.Google Scholar
[28]Schmidt-Pruzan, J. and Shamir, E. (1985) Component structure in the evolution of random hypergraphs. Combinatorica 5 81–94.Google Scholar
[29]Stepanov, V. E. (1970) On the probability of connectedness of a random graph gm(t). Theory Probab. Appl. 15 55–67.Google Scholar