Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-28T13:05:45.664Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Resilience and Hamiltonicity Maker–Breaker Games in Random Regular Graphs

Published online by Cambridge University Press:  16 December 2010

SONNY BEN-SHIMON ,
MICHAEL KRIVELEVICH  and
BENNY SUDAKOV
SONNY BEN-SHIMON
Affiliation:
School of Computer Science, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv 69978, Israel (e-mail: sonny@tau.ac.il)
MICHAEL KRIVELEVICH
Affiliation:
School of Mathematical Sciences, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv 69978, Israel (e-mail: krivelev@tau.ac.il)
BENNY SUDAKOV
Affiliation:
Department of Mathematics, UCLA, Los Angles 90005, CA, USA (e-mail: bsudakov@math.ucla.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

For an increasing monotone graph property 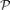the local resilience of a graph G with respect to 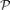is the minimal r for which there exists a subgraph H ⊆ G with all degrees at most r, such that the removal of the edges of H from G creates a graph that does not possess 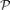. This notion, which was implicitly studied for some ad hoc properties, was recently treated in a more systematic way in a paper by Sudakov and Vu. Most research conducted with respect to this distance notion focused on the binomial random graph model 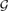(n, p) and some families of pseudo-random graphs with respect to several graph properties, such as containing a perfect matching and being Hamiltonian, to name a few. In this paper we continue to explore the local resilience notion, but turn our attention to random and pseudo-random regular graphs of constant degree. We investigate the local resilience of the typical random d-regular graph with respect to edge and vertex connectivity, containing a perfect matching, and being Hamiltonian. In particular, we prove that for every positive ϵ and large enough values of d, with high probability, the local resilience of the random d-regular graph, 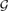n, d, with respect to being Hamiltonian, is at least (1−ϵ)d/6. We also prove that for the binomial random graph model 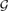(n, p), for every positive ϵ > 0 and large enough values of K, if p > 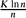then, with high probability, the local resilience of 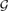(n, p) with respect to being Hamiltonian is at least (1−ϵ)np/6. Finally, we apply similar techniques to positional games, and prove that if d is large enough then, with high probability, a typical random d-regular graph G is such that, in the unbiased Maker–Breaker game played on the edges of G, Maker has a winning strategy to create a Hamilton cycle.

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 2 , March 2011 , pp. 173 - 211
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, third edition, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley.CrossRefGoogle Scholar
[2]Beck, J. (2008) Combinatorial Games: Tic-Tac-Toe Theory, Cambridge University Press.CrossRefGoogle Scholar
[3]Bollobás, B. (1981) Random graphs. In Combinatorics (Temperley, H. N. V., ed.), Vol. 52 of London Mathematical Society Lecture Notes, Cambridge University Press, pp. 80–102.CrossRefGoogle Scholar
[4]Bollobás, B. (1983) Almost all regular graphs are Hamiltonian. Europ. J. Combin. 4 94–106.CrossRefGoogle Scholar
[5]Bollobás, B. (2001) Random Graphs, Cambridge University Press.CrossRefGoogle Scholar
[6]Broder, A., Frieze, A., Suen, S. and Upfal, E. (1999) Optimal construction of edge-disjoint paths in random graphs. SIAM J. Comput. 28 541–573.CrossRefGoogle Scholar
[7]Chung, F. (2004) Discrete isoperimetric inequalities. In Surveys in Differential Geometry: Eigenvalues of Laplacians and Other Geometric Operators (Grigor'yan, A. and Yau, S. T., eds), Vol. IX, International Press.Google Scholar
[8]Chvátal, V. and Erdős, P. (1978) Biased positional games. Ann. Discrete Math. 2 221–228.CrossRefGoogle Scholar
[9]Dellamonica, D., Kohayakawa, Y., Marciniszyn, M. and Steger, A. (2008) On the resilience of long cycles in random graphs. Electron. J. Combin. 15 R32.CrossRefGoogle Scholar
[10]Diestel, R. (2005) Graph Theory, third edition, Vol. 173 of Graduate Texts in Mathematics, Springer.Google Scholar
[11]Fenner, T. and Frieze, A. (1984) Hamiltonian cycles in random regular graphs. J. Combin. Theory Ser. B 37 103–198.CrossRefGoogle Scholar
[12]Friedman, J. (2008) A proof of Alon's second eigenvalue conjecture and related problems. Mem. Amer. Math. Soc. 195 (910).Google Scholar
[13]Frieze, A. (1988) Finding Hamilton cycles in sparse random graphs. J. Combin. Theory Ser. B 44 230–250.CrossRefGoogle Scholar
[14]Frieze, A. and Krivelevich, M. (2008) On two Hamiltonian cycle problems in random graphs. Israel J. Math. 166 221–234.CrossRefGoogle Scholar
[15]Greenhill, C., Kim, J. H., Janson, S. and Wormald, N. C. (2002) Permutation pseudographs and contiguity. Combin. Probab. Comput. 11 273–298.CrossRefGoogle Scholar
[16]Hefetz, D., Krivelevich, M., Stojaković, M. and Szabó, T. (2009) A sharp threshold for the Hamilton cycle Maker–Breaker game. Random Struct. Alg. 34 112–122.CrossRefGoogle Scholar
[17]Hefetz, D., Krivelevich, M., Stojaković, M. and Szabó, T. Global Maker-Breaker games on sparse graphs. Europ. J. Combin., to appear.Google Scholar
[18]Hefetz, D., Krivelevich, M. and Szabó, T. (2009) Hamilton cycles in highly connected and expanding graphs. Combinatorica 29 547–568.CrossRefGoogle Scholar
[19]Hefetz, D. and Stich, S. (2009) On two problems regarding the Hamilton cycle game. Electron. J. Combin. 16 R28.CrossRefGoogle Scholar
[20]Janson, S. (1995) Random regular graphs: Asymptotic distributions and contiguity. Combin. Probab. Comput. 4 369–405.CrossRefGoogle Scholar
[21]Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley.CrossRefGoogle Scholar
[22]Kim, J. H., Sudakov, B. and Vu, V. H. (2002) On the asymmetry of random regular graphs. Random Struct. Alg. 21 216–224.CrossRefGoogle Scholar
[23]Kim, J. H., Sudakov, B. and Vu, V. H. (2007) Small subgraphs of random regular graphs. Discrete Math. 307 1961–1967.CrossRefGoogle Scholar
[24]Kim, J. H. and Vu, V. H. (2004) Sandwiching random graphs. Adv. Math. 188 444–469.CrossRefGoogle Scholar
[25]Kim, J. H. and Wormald, N. C. (2001) Random matchings which induce Hamilton cycles, and Hamiltonian decompositions of random regular graphs. J. Combin. Theory Ser. B 81 20–44.CrossRefGoogle Scholar
[26]Krivelevich, M., Lee, C. and Sudakov, B. (2010) Resilient pancyclicity of random and pseudo-random graphs. SIAM J. Discrete Math. 24 1–16.CrossRefGoogle Scholar
[27]Krivelevich, M. and Sudakov, B. (2003) Sparse pseudo-random graphs are Hamiltonian. J. Graph Theory 42 17–33.CrossRefGoogle Scholar
[28]Krivelevich, M. and Sudakov, B. (2006) Pseudo-random graphs. In More Sets, Graphs and Numbers: A Salute to Vera Sòs and András Hajnal (Győri, E., Katona, G. O. H. and Lovász, L., eds), Vol. 15 of Bolyai Society Mathematical Studies, Springer, pp. 199–262.CrossRefGoogle Scholar
[29]Krivelevich, M., Sudakov, B., Vu, V. H. and Wormald, N. (2001) Random regular graphs of high degree. Random Struct. Alg. 18 346–363.CrossRefGoogle Scholar
[30]Lehman, A. (1964) A solution of the Shannon switching game. J. Soc. Ind. Appl. Math. 12 687–725.CrossRefGoogle Scholar
[31]McDiarmid, C. (1998) Concentration. In Probabilistic Methods for Algorithmic Discrete Mathematics (Habib, M., McDiarmid, C., Ramirez-Alfonsin, J. and Reed, B., eds), Springer, pp. 195–248.CrossRefGoogle Scholar
[32]McKay, B. D. (1985) Asymptotics for symmetric 0–1 matrices with prescribed row sums. Ars Combinatorica 19 15–26.Google Scholar
[33]Nilli, A. (1991) On the second eigenvalue of a graph. Discrete Math. 91 207–210.CrossRefGoogle Scholar
[34]Pósa, L. (1976) Hamiltonian circuits in random graphs. Discrete Math. 14 359–364.CrossRefGoogle Scholar
[35]Robinson, R. and Wormald, N. (1992) Almost all cubic graphs are Hamiltonian. Random Struct. Alg. 3 117–125.CrossRefGoogle Scholar
[36]Robinson, R. and Wormald, N. (1994) Almost all regular graphs are Hamiltonian. Random Struct. Alg. 5 363–374.CrossRefGoogle Scholar
[37]Sudakov, B. and Vu, V. H. (2008) The local resilience of random graphs. Random Struct. Alg. 33 409–433.CrossRefGoogle Scholar
[38]Turán, P. (1941) Eine Extremalaufgabe aus der Graphentheorie. Mat. Fiz. Lapok 48 436–452.Google Scholar
[39]Wormald, N. C. (1981) The asymptotic connectivity of labelled regular graphs. J. Combin. Theory Ser. B 31 156–167.CrossRefGoogle Scholar
[40]Wormald, N. C. (1999) Models of random regular graphs. In Surveys in Combinatorics (Lamb, J. and Preece, D., eds), Vol. 276 of London Mathematical Society Lecture Notes, Cambridge University Press, pp. 239–298.Google Scholar