Article contents
Minimizing the number of 5-cycles in graphs with given edge-density
Published online by Cambridge University Press: 09 October 2019
Abstract
Motivated by the work of Razborov about the minimal density of triangles in graphs we study the minimal density of the 5-cycle C5. We show that every graph of order n and size 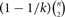 $ (1 - 1/k) \left( {\matrix{n \cr 2 }} \right) $, where k ≥ 3 is an integer, contains at least
$ (1 - 1/k) \left( {\matrix{n \cr 2 }} \right) $, where k ≥ 3 is an integer, contains at least $$({1 \over {10}} - {1 \over {2k}} + {1 \over {{k^2}}} - {1 \over {{k^3}}} + {2 \over {5{k^4}}}){n^5} + o({n^5})$$
$$({1 \over {10}} - {1 \over {2k}} + {1 \over {{k^2}}} - {1 \over {{k^3}}} + {2 \over {5{k^4}}}){n^5} + o({n^5})$$
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
Supported in part by Simons Foundation grant 426894.
Supported in part by Simons Foundation grant 522400.
Supported in part by NSF grant DMS-1600390.
Supported in part by ERC grant 306493.
References
- 3
- Cited by

