Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aistleitner, Christoph
2014.
On the limit distribution of the normality measure of random binary sequences.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 5,
p.
968.

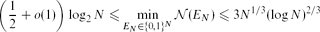
 (
(