Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-25T01:00:15.086Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Universal and Canonically Coloured Sequences

Published online by Cambridge University Press:  01 September 2009

ANDRZEJ DUDEK ,
PETER FRANKL  and
VOJTĚCH RÖDL
ANDRZEJ DUDEK
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA (e-mail: adudek@andrew.cmu.edu)
PETER FRANKL
Affiliation:
Peter Frankl Office, Ltd., 3-12-25 Shibuya, Shibuya-ku, Tokyo 150-0002, Japan (e-mail: Peter111F@aol.com)
VOJTĚCH RÖDL
Affiliation:
Department of Mathematics and Computer Science, Emory University, Atlanta, GA 30322, USA (e-mail: rodl@mathcs.emory.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

A sequence X = {xi}ni=1 over an alphabet containing t symbols is t-universal if every permutation of those symbols is contained as a subsequence. Kleitman and Kwiatkowski showed that the minimum length of a t-universal sequence is (1 − o(1))t2. In this note we address a related Ramsey-type problem. We say that an r-colouring χ of the sequence X is canonical if χ(xi) = χ(xj) whenever xi = xj. We prove that for any fixedt the length of the shortest sequence over an alphabet of size t, which has the property that every r-colouring of its entries contains a t-universal and canonically coloured subsequence, is at most 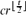. This is best possible up to a multiplicative constant c independent of r.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 5: New Directions in Algorithms, Combinatorics and Optimization , September 2009 , pp. 683 - 689
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Kleitman, D. J. and Kwiatkowski, D. J. (1976) A lower bound on the length of a sequence containing all permutations as subsequences. J. Combin. Theory Ser. A 21 129–136.CrossRefGoogle Scholar
[2]Koutas, P. J. and Hu, T. C. (1975) Shortest string containing all permutations. Discrete Math. 11 125–132.CrossRefGoogle Scholar
[3]Mohanty, S. P. (1980) Shortest string containing all permutations. Discrete Math. 31 91–95.CrossRefGoogle Scholar
[4]Newey, M. C. (1973) Notes on a problem involving permutations as subsequences. Computer Science Department Report, CS-73-340 Stanford University, Stanford, CA.Google Scholar