The Ramsey number, 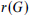, of a graph G is the minimum integer N such that, in every 2-colouring of the edges of the complete graph 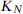on N vertices, there is a monochromatic copy of G. In 1975, Burr and Erdős posed a problem on Ramsey numbers of d-degenerate graphs, i.e., graphs in which every subgraph has a vertex of degree at most d. They conjectured that for every d there exists a constant c(d) such that for any d-degenerate graph G of order n.

In this paper we prove that 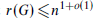for each such G. In fact, we show that, for every , sufficiently large n, and any graph H of order 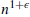, either H or its complement contains a (d,n)-common graph, that is, a graph in which every set of d vertices has at least n common neighbours. It is easy to see that any (d,n)-common graph contains every d-degenerate graph G of order n. We further show that, for every constant C, there is an n and a graph H of order 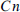such that neither H nor its complement contains a 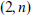-common graph.