Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Achlioptas, Dimitris
Kirousis, Lefteris M.
Kranakis, Evangelos
Krizanc, Danny
Molloy, Michael S. O.
and
Stamatiou, Yannis C.
1997.
Principles and Practice of Constraint Programming-CP97.
Vol. 1330,
Issue. ,
p.
107.
Achlioptas, Dimitris
2000.
Setting 2 variables at a time yields a new lower bound for random 3-SAT (extended abstract).
p.
28.
Achlioptas, Dimitris
Kirousis, Lefteris M.
Kranakis, Evangelos
and
Krizanc, Danny
2001.
Rigorous results for random (2+p)-SAT.
Theoretical Computer Science,
Vol. 265,
Issue. 1-2,
p.
109.
Dubois, Olivier
2001.
Upper bounds on the satisfiability threshold.
Theoretical Computer Science,
Vol. 265,
Issue. 1-2,
p.
187.
Achlioptas, Dimitris
Molloy, Michael S. O.
Kirousis, Lefteris M.
Stamatiou, Yannis C.
Kranakis, Evangelos
and
Krizanc, Danny
2001.
Random Constraint Satisfaction: A More Accurate Picture.
Constraints,
Vol. 6,
Issue. 4,
p.
329.
Bollobás, Béla
Borgs, Christian
Chayes, Jennifer T.
Kim, Jeong Han
and
Wilson, David B.
2001.
The scaling window of the 2‐SAT transition.
Random Structures & Algorithms,
Vol. 18,
Issue. 3,
p.
201.
Kaporis, Alexis C.
Kirousis, Lefteris M.
and
Lalas, Efthimios G.
2002.
Algorithms — ESA 2002.
Vol. 2461,
Issue. ,
p.
574.
Achlioptas, D.
and
Moore, C.
2002.
The asymptotic order of the random k-SAT threshold.
p.
779.
Kaporis, Alexis C.
Kirousis, Lefteris M.
and
Lalas, Efthimios
2003.
Selecting Complementary Pairs of Literals.
Electronic Notes in Discrete Mathematics,
Vol. 16,
Issue. ,
p.
47.
Franco, John
and
Swaminathan, Ram
2003.
On good algorithms for determining unsatisfiability of propositional formulas.
Discrete Applied Mathematics,
Vol. 130,
Issue. 2,
p.
129.
Franco, John
2005.
Typical case complexity of Satisfiability Algorithms and the threshold phenomenon.
Discrete Applied Mathematics,
Vol. 153,
Issue. 1-3,
p.
89.
Plagne, Alain
2006.
On threshold properties ofk-SAT: An additive viewpoint.
European Journal of Combinatorics,
Vol. 27,
Issue. 7,
p.
1186.
Achlioptas, Dimitris
and
Moore, Cristopher
2006.
Random k‐SAT: Two Moments Suffice to Cross a Sharp Threshold.
SIAM Journal on Computing,
Vol. 36,
Issue. 3,
p.
740.
Fernandez de la Vega, Wenceslas
and
Karpinski, Marek
2007.
1.0957-Approximation Algorithm for Random MAX-3SAT.
RAIRO - Operations Research,
Vol. 41,
Issue. 1,
p.
95.
Boufkhad, Yacine
and
Hugel, Thomas
2010.
Theory and Applications of Satisfiability Testing – SAT 2010.
Vol. 6175,
Issue. ,
p.
99.

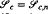 be the set of all such
be the set of all such 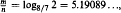 , that if
, that if 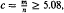 , then almost all
, then almost all 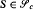 are unsatisfiable.
are unsatisfiable.