Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-27T15:42:46.623Z Has data issue: false hasContentIssue false
  • English
  • Français

On the maximum number of edges in 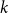$k$-critical graphs

Part of: Graph theory

Published online by Cambridge University Press:  24 July 2023

Cong Luo ,
Jie Ma  and
Tianchi Yang
Cong Luo
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, China
Jie Ma
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, China
Tianchi Yang*
Affiliation:
Department of Mathematics, National University of Singapore, Singapore, Singapore
*
Corresponding author: Tianchi Yang; Email: tcyang@nus.edu.sg
Get access Rights & Permissions [Opens in a new window]

Abstract

A graph is called 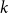$k$-critical if its chromatic number is 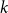$k$ but every proper subgraph has chromatic number less than 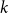$k$. An old and important problem in graph theory asks to determine the maximum number of edges in an $n$-vertex 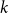$k$-critical graph. This is widely open for every integer 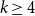$k\geq 4$. Using a structural characterisation of Greenwell and Lovász and an extremal result of Simonovits, Stiebitz proved in 1987 that for 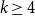$k\geq 4$ and sufficiently large $n$, this maximum number is less than the number of edges in the $n$-vertex balanced complete 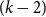$(k-2)$-partite graph. In this paper, we obtain the first improvement in the above result in the past 35 years. Our proofs combine arguments from extremal graph theory as well as some structural analysis. A key lemma we use indicates a partial structure in dense 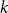$k$-critical graphs, which may be of independent interest.

Keywords

critical graphs

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 6 , November 2023 , pp. 900 - 911
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, H. L. and Zhou, B. (1992) On a conjecture of Gallai concerning complete subgraphs of $k$ -critical graphs. Discrete Math. 100 223–228.CrossRefGoogle Scholar
Dirac, G. A. (1952) A property of 4-chromatic graphs and some remarks on critical graphs. J. London Math. Soc. 27(1) 85–92.CrossRefGoogle Scholar
Füredi, Z. (2015) A proof of the stability of extremal graphs, Simonovits’ stability from Szemerédi’s regularity. J. Combin. Theory Ser. B 115 66–71.CrossRefGoogle Scholar
Gao, J. and Ma, J. (2023) Tight bounds towards a conjecture of Gallai. Combinatorica, to appear. DOI: 10.1007/s00493-023-00020-z.CrossRefGoogle Scholar
Greenwell, D. and Lovász, L. (1974) Applications of product colouring. Acta Math. Acad. Sci. Hungar. 25(3-4) 335–340.CrossRefGoogle Scholar
Jensen, T. R. and Toft, B. (1995) Graph coloring problems. Wiley-Interscience Series in Discrete Mathematics and Optimization. John Wiley & Sons, Inc., New York: A Wiley-Interscience Publication. Google Scholar
Kézdy, A. E. and Snevily, H. S. (1997) On extensions of a conjecture of Gallai. J. Combin. Theory Ser. B 70(2) 317–324.10.1006/jctb.1997.1764CrossRefGoogle Scholar
Pegden, W. (2013) Critical graphs without triangles: an optimum density construction. Combinatorica 33(4) 495–512.CrossRefGoogle Scholar
Reiman, I. (1958) Über ein Problem von K. Zarankiewicz. Acta Math. Acad. Sci. Hungar. 9(3-4) 269–273.CrossRefGoogle Scholar
Simonovits, M. (1968) A method for solving extremal problems in graph theory, stability problems. In Theory of Graphs (Proc. Colloq. Tihany, 1966), New York: Academic Press.Google Scholar
Stiebitz, M. (1987) Subgraphs of colour-critical graphs. Combinatorica 7(3) 303–312.CrossRefGoogle Scholar
Toft, B. (1970) On the maximal number of edges of critical $k$ -chromatic graphs. Studia Sci. Math. Hungar. 5 461–470.Google Scholar