Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McDiarmid, Colin
and
Yolov, Nikola
2019.
Random perfect graphs.
Random Structures & Algorithms,
Vol. 54,
Issue. 1,
p.
148.

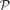

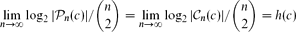
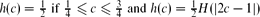 otherwise, where
otherwise, where 