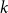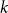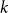1. Introduction
A widely studied generalisation of the notion of a Hamilton cycle is that of the
![]() $k$
th power of a Hamilton cycle: the
$k$
th power of a Hamilton cycle: the
![]() $k$
th power of a Hamilton cycle
$k$
th power of a Hamilton cycle
![]() $C$
is obtained from
$C$
is obtained from
![]() $C$
by adding an edge between every pair of vertices of distance at most
$C$
by adding an edge between every pair of vertices of distance at most
![]() $k$
on
$k$
on
![]() $C$
. We usually call the
$C$
. We usually call the
![]() $2$
nd power of a Hamilton cycle the square of a Hamilton cycle. As well as being natural objects in their own right, finding the
$2$
nd power of a Hamilton cycle the square of a Hamilton cycle. As well as being natural objects in their own right, finding the
![]() $k$
th power of a Hamilton cycle in a graph
$k$
th power of a Hamilton cycle in a graph
![]() $G$
ensures that
$G$
ensures that
![]() $G$
contains other well-studied graph structures. For example, an
$G$
contains other well-studied graph structures. For example, an
![]() $n$
-vertex square of a Hamilton cycle contains every possible collection of vertex-disjoint paths and cycles on
$n$
-vertex square of a Hamilton cycle contains every possible collection of vertex-disjoint paths and cycles on
![]() $n$
vertices. Further, if
$n$
vertices. Further, if
![]() $k+1$
divides
$k+1$
divides
![]() $n$
, then an
$n$
, then an
![]() $n$
-vertex
$n$
-vertex
![]() $k$
th power of a Hamilton cycle contains a
$k$
th power of a Hamilton cycle contains a
![]() $K_{k+1}$
-factor.Footnote
1
Powers of Hamilton cycles have also been used as the ‘building blocks’ for proving several bandwidth theorems; see, for example, [Reference Böttcher, Schacht and Taraz5, Reference Ebsen, Maesaka, Reiher, Schacht and Schülke11, Reference Staden and Treglown34].
$K_{k+1}$
-factor.Footnote
1
Powers of Hamilton cycles have also been used as the ‘building blocks’ for proving several bandwidth theorems; see, for example, [Reference Böttcher, Schacht and Taraz5, Reference Ebsen, Maesaka, Reiher, Schacht and Schülke11, Reference Staden and Treglown34].
A major branch of extremal graph theory concerns minimum degree conditions that force a spanning structure in a graph. For example, Dirac’s theorem asserts that every graph
![]() $G$
on
$G$
on
![]() $n \geq 3$
vertices and of minimum degree
$n \geq 3$
vertices and of minimum degree
![]() $\delta (G) \geq n/2$
contains a Hamilton cycle. The following famous conjecture provides a generalisation of Dirac’s theorem to powers of Hamilton cycles.
$\delta (G) \geq n/2$
contains a Hamilton cycle. The following famous conjecture provides a generalisation of Dirac’s theorem to powers of Hamilton cycles.
Conjecture 1.1 (Pósa and Seymour, see [Reference Erdős and Fieldler12, Reference Seymour33]). Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $n\geq k\geq 2$
vertices. If
$n\geq k\geq 2$
vertices. If
![]() $\delta (G) \geq \frac {k}{k+1} n$
then
$\delta (G) \geq \frac {k}{k+1} n$
then
![]() $G$
contains the
$G$
contains the
![]() $k$
th power of a Hamilton cycle.
$k$
th power of a Hamilton cycle.
Note that the minimum degree condition in Conjecture 1.1 cannot be lowered. Indeed, in the case when
![]() $k+1$
divides
$k+1$
divides
![]() $n$
, consider the complete
$n$
, consider the complete
![]() $(k+1)$
-partite graph
$(k+1)$
-partite graph
![]() $G$
in which all but two classes have size
$G$
in which all but two classes have size
![]() $n/(k+1)$
, one class has size
$n/(k+1)$
, one class has size
![]() $n/(k+1)+1$
, and the last class has size
$n/(k+1)+1$
, and the last class has size
![]() $n/(k+1)-1$
. Then
$n/(k+1)-1$
. Then
![]() $G$
does not contain a
$G$
does not contain a
![]() $K_{k+1}$
-factor and
$K_{k+1}$
-factor and
![]() $\delta (G)=kn/(k+1)-1$
.
$\delta (G)=kn/(k+1)-1$
.
Whilst Pósa’s conjecture (the
![]() $k=2$
case) was posed in the early 1960s, and Seymour’s conjecture (for arbitrary
$k=2$
case) was posed in the early 1960s, and Seymour’s conjecture (for arbitrary
![]() $k$
) in 1974, it was not until the 1990s that significant progress was made on the problem. Indeed, after several partial results towards the Pósa–Seymour conjecture (see, e.g. [Reference Fan and Häggkvist14–Reference Faudree, Gould, Jacobson, Schelp and Kulli18, Reference Komlós, Sárközy and Szemerédi24, Reference Komlós, Sárközy and Szemerédi26]), Komlós, Sárközy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi27] applied Szemerédi’s regularity lemma to prove Conjecture 1.1 for sufficiently large graphs. Subsequently, proofs of Pósa’s conjecture for large graphs have been obtained that avoid the regularity lemma [Reference Châu, DeBiasio and Kierstead7, Reference Levitt, Sárközy and Szemerédi28].
$k$
) in 1974, it was not until the 1990s that significant progress was made on the problem. Indeed, after several partial results towards the Pósa–Seymour conjecture (see, e.g. [Reference Fan and Häggkvist14–Reference Faudree, Gould, Jacobson, Schelp and Kulli18, Reference Komlós, Sárközy and Szemerédi24, Reference Komlós, Sárközy and Szemerédi26]), Komlós, Sárközy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi27] applied Szemerédi’s regularity lemma to prove Conjecture 1.1 for sufficiently large graphs. Subsequently, proofs of Pósa’s conjecture for large graphs have been obtained that avoid the regularity lemma [Reference Châu, DeBiasio and Kierstead7, Reference Levitt, Sárközy and Szemerédi28].
1.1 Powers of Hamilton cycles in digraphs
It is also natural to study powers of Hamilton cycles in directed graphs. Recall that digraphs are graphs such that every pair of vertices has at most two edges between them, at most one oriented in each direction. Oriented graphs are orientations of simple graphs; so there is at most one directed edge between any pair of vertices. A tournament is an oriented complete graph. Note that oriented graphs are a subclass of digraphs. In this setting, the
![]() $k$
th power of a Hamilton cycle
$k$
th power of a Hamilton cycle
![]() $C$
is the digraph obtained from
$C$
is the digraph obtained from
![]() $C$
by adding a directed edge from
$C$
by adding a directed edge from
![]() $x$
to
$x$
to
![]() $y$
if there is a directed path of length at most
$y$
if there is a directed path of length at most
![]() $k$
from
$k$
from
![]() $x$
to
$x$
to
![]() $y$
on
$y$
on
![]() $C$
.
$C$
.
Given a digraph
![]() $G$
and
$G$
and
![]() $x \in V(G)$
, we write
$x \in V(G)$
, we write
![]() $d^+_G(x)$
(or simply
$d^+_G(x)$
(or simply
![]() $d^+(x)$
) for the outdegree of
$d^+(x)$
) for the outdegree of
![]() $x$
in
$x$
in
![]() $G$
and
$G$
and
![]() $d^-_G(x)$
(or simply
$d^-_G(x)$
(or simply
![]() $d^-(x)$
) for the indegree of
$d^-(x)$
) for the indegree of
![]() $x$
in
$x$
in
![]() $G$
. The minimum semi-degree
$G$
. The minimum semi-degree
![]() $\delta ^0(G)$
of
$\delta ^0(G)$
of
![]() $G$
is the minimum of all the in- and outdegrees of the vertices in
$G$
is the minimum of all the in- and outdegrees of the vertices in
![]() $G$
. The minimum total degree
$G$
. The minimum total degree
![]() $\delta (G)$
is the minimum number of edges incident to a vertex in
$\delta (G)$
is the minimum number of edges incident to a vertex in
![]() $G$
. Ghouila-Houri [Reference Ghouila-Houri21] proved that every strongly connected
$G$
. Ghouila-Houri [Reference Ghouila-Houri21] proved that every strongly connected
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with minimum total degree
$G$
with minimum total degree
![]() $\delta (G)\geq n$
contains a Hamilton cycle. Note that there are
$\delta (G)\geq n$
contains a Hamilton cycle. Note that there are
![]() $n$
-vertex digraphs
$n$
-vertex digraphs
![]() $G$
with
$G$
with
![]() $\delta (G) = \lfloor 3n/2\rfloor - 2$
that are not strongly connected (and thus do not contain a Hamilton cycle), so the strongly connected condition in Ghouila-Houri’s theorem is necessary.Footnote
2
An immediate consequence of Ghouila-Houri’s theorem is that having minimum semi-degree
$\delta (G) = \lfloor 3n/2\rfloor - 2$
that are not strongly connected (and thus do not contain a Hamilton cycle), so the strongly connected condition in Ghouila-Houri’s theorem is necessary.Footnote
2
An immediate consequence of Ghouila-Houri’s theorem is that having minimum semi-degree
![]() $\delta ^0(G) \geq n/2$
forces a Hamilton cycle, and this is best possible.
$\delta ^0(G) \geq n/2$
forces a Hamilton cycle, and this is best possible.
The problem of determining the minimum semi-degree threshold that forces the
![]() $k$
th power of a Hamilton cycle in a digraph was raised in [Reference Treglown35]. Indeed, as stated in [Reference Treglown35], one would expect a positive answer to the following question.
$k$
th power of a Hamilton cycle in a digraph was raised in [Reference Treglown35]. Indeed, as stated in [Reference Treglown35], one would expect a positive answer to the following question.
Question 1.2.
Does every
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with
$G$
with
![]() $\delta ^0 (G) \geq \frac {k}{k+1}n$
contain the
$\delta ^0 (G) \geq \frac {k}{k+1}n$
contain the
![]() $k$
th power of a Hamilton cycle?
$k$
th power of a Hamilton cycle?
By replacing edges with ‘double edges’ in the extremal example of the Pósa–Seymour conjecture, one can see that, if true, the minimum semi-degree condition in Question 1.2 would be tight. Question 1.2 does seem to be rather challenging, and we are unaware of any progress on the problem.
An aim of this paper is to raise the analogous question for the minimum total degree threshold; we propose the following conjecture.
Conjecture 1.3.
Let
![]() $k \in \mathbb{N}$
and suppose
$k \in \mathbb{N}$
and suppose
![]() $n \in \mathbb N$
is sufficiently large. Write
$n \in \mathbb N$
is sufficiently large. Write
![]() $n=(k+3)q+r$
where
$n=(k+3)q+r$
where
![]() $q,r \in \mathbb Z$
and
$q,r \in \mathbb Z$
and
![]() $0\leq r\leq k+2$
. Every
$0\leq r\leq k+2$
. Every
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with
$G$
with
 \begin{align*} \delta (G)\geq \begin{cases} 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -3 & \text{ if } r = k+2 ,\\[6pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -2 & \text{ if } r = k \text{ or } r=k+1 , \\[6pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -1 & \text{ otherwise,} \\ \end{cases} \end{align*}
\begin{align*} \delta (G)\geq \begin{cases} 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -3 & \text{ if } r = k+2 ,\\[6pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -2 & \text{ if } r = k \text{ or } r=k+1 , \\[6pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -1 & \text{ otherwise,} \\ \end{cases} \end{align*}
contains the
![]() $k$
th power of a Hamilton cycle.
$k$
th power of a Hamilton cycle.
In Section 3, we provide an extremal example that shows, if true, the minimum total degree condition in Conjecture 1.3 is best possible (see Proposition 3.1). Also note that Ghouila-Houri’s theorem implies that Conjecture 1.3 holds for
![]() $k=1$
since an
$k=1$
since an
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with
$G$
with
![]() $\delta (G)\geq \lfloor \frac {3n}{2}\rfloor -1$
is strongly connected. On this note, one may wonder if it is possible to significantly relax the minimum total degree condition in Conjecture 1.3 at the expense of introducing some strong connectivity condition (perhaps of a similar form to the conclusion of the statement of Lemma 5.14). We suspect that this is true and, moreover, further progress on Conjecture 1.3 is likely to provide insight into precisely what form such a statement should take.
$\delta (G)\geq \lfloor \frac {3n}{2}\rfloor -1$
is strongly connected. On this note, one may wonder if it is possible to significantly relax the minimum total degree condition in Conjecture 1.3 at the expense of introducing some strong connectivity condition (perhaps of a similar form to the conclusion of the statement of Lemma 5.14). We suspect that this is true and, moreover, further progress on Conjecture 1.3 is likely to provide insight into precisely what form such a statement should take.
Our first result yields an asymptotic version of Conjecture 1.3 in the case of the square of a Hamilton cycle (i.e.
![]() $k=2$
).
$k=2$
).
Theorem 1.4.
Given any
![]() $\eta \gt 0$
, there exists
$\eta \gt 0$
, there exists
![]() $n_0 \in \mathbb N$
so that for any
$n_0 \in \mathbb N$
so that for any
![]() $n \geq n_0$
, the following holds. If
$n \geq n_0$
, the following holds. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex digraph with
$n$
-vertex digraph with
then
![]() $G$
contains the square of a Hamilton cycle.
$G$
contains the square of a Hamilton cycle.
In Section 8.1, we explain why we believe it challenging to generalise Theorem1.4 to an asymptotic solution of Conjecture 1.3 for all
![]() $k \in \mathbb N$
. In particular, whilst some of our auxiliary results for Theorem1.4 apply to this more general question, the main stumbling block is establishing a suitable connecting lemma.
$k \in \mathbb N$
. In particular, whilst some of our auxiliary results for Theorem1.4 apply to this more general question, the main stumbling block is establishing a suitable connecting lemma.
1.2 Powers of Hamilton cycles in oriented graphs
There has also been interest in powers of Hamilton cycles in oriented graphs. In this setting, the emphasis has been on the study of minimum semi-degree results rather than minimum total degree results; this is natural since if
![]() $G$
is an
$G$
is an
![]() $n$
-vertex transitive tournament, then
$n$
-vertex transitive tournament, then
![]() $\delta (G)=n-1$
and
$\delta (G)=n-1$
and
![]() $G$
does not contain a (power of a) Hamilton cycle.
$G$
does not contain a (power of a) Hamilton cycle.
Answering a question of Thomassen from 1979, Keevash, Kühn, and Osthus [Reference Keevash, Kühn and Osthus22] proved that every sufficiently large
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
![]() $\delta ^0 (G) \geq (3n - 4)/8$
contains a Hamilton cycle. Moreover, the minimum semi-degree condition here cannot be lowered.
$\delta ^0 (G) \geq (3n - 4)/8$
contains a Hamilton cycle. Moreover, the minimum semi-degree condition here cannot be lowered.
The second goal of this paper is to study the minimum semi-degree threshold for forcing the
![]() $k$
th power of a Hamilton cycle in an oriented graph.
$k$
th power of a Hamilton cycle in an oriented graph.
When
![]() $G$
is a tournament, then much is known. As discussed in [Reference Draganić, Munhá Correia and Sudakov10], every
$G$
is a tournament, then much is known. As discussed in [Reference Draganić, Munhá Correia and Sudakov10], every
![]() $n$
-vertex tournament
$n$
-vertex tournament
![]() $G$
with
$G$
with
![]() $\delta ^0 (G) \geq (n-2)/4$
contains a Hamilton cycle, and this degree condition is best possible. Bollobás and Häggkvist [Reference Bollobás and Häggkvist4] proved that actually one only needs to boost the minimum semi-degree slightly to force the
$\delta ^0 (G) \geq (n-2)/4$
contains a Hamilton cycle, and this degree condition is best possible. Bollobás and Häggkvist [Reference Bollobás and Häggkvist4] proved that actually one only needs to boost the minimum semi-degree slightly to force the
![]() $k$
th power of a Hamilton cycle: that is, for a fixed
$k$
th power of a Hamilton cycle: that is, for a fixed
![]() $k \in \mathbb N$
,
$k \in \mathbb N$
,
![]() $\delta ^0 (G) \geq (1+o(1))n/4$
ensures the
$\delta ^0 (G) \geq (1+o(1))n/4$
ensures the
![]() $k$
th power of a Hamilton cycle in an
$k$
th power of a Hamilton cycle in an
![]() $n$
-vertex tournament
$n$
-vertex tournament
![]() $G$
. This result has recently been significantly refined by Draganić, Munhá Correia, and Sudakov [Reference Draganić, Munhá Correia and Sudakov10], who proved that one can take
$G$
. This result has recently been significantly refined by Draganić, Munhá Correia, and Sudakov [Reference Draganić, Munhá Correia and Sudakov10], who proved that one can take
![]() $\delta ^0 (G) \geq n/4+ cn^{1-1/\lceil k/2 \rceil }$
here, for some constant
$\delta ^0 (G) \geq n/4+ cn^{1-1/\lceil k/2 \rceil }$
here, for some constant
![]() $c=c(k)$
.
$c=c(k)$
.
Draganić, Dross, Fox, Girão, Havet, Korándi, Lochet, Munhá Correia, Scott, and Sudakov [Reference Draganić, Dross and Fox9] proved that every tournament contains the
![]() $k$
th power of path of length at least
$k$
th power of path of length at least
![]() $\frac {n}{2^{4k+6}k}$
which is close to best possible since there are tournaments where the longest
$\frac {n}{2^{4k+6}k}$
which is close to best possible since there are tournaments where the longest
![]() $k$
th power of path has length less than
$k$
th power of path has length less than
![]() $\frac {k(k+1)n}{2^k}$
. They also proved an exact result for square paths; that is, every tournament contains a square path of length at least
$\frac {k(k+1)n}{2^k}$
. They also proved an exact result for square paths; that is, every tournament contains a square path of length at least
![]() $\lceil 2n/3\rceil -1$
, and this is best possible.
$\lceil 2n/3\rceil -1$
, and this is best possible.
For oriented graphs that are not tournaments, essentially nothing is known about
![]() $k$
th powers of paths and cycles (whether it be short cycles or Hamilton cycles). Until now, it has not even been proven that a minimum semi-degree of
$k$
th powers of paths and cycles (whether it be short cycles or Hamilton cycles). Until now, it has not even been proven that a minimum semi-degree of
![]() $\delta ^0 (G) \geq (1-\varepsilon )n/2$
suffices to force the square of a Hamilton cycle (for some tiny
$\delta ^0 (G) \geq (1-\varepsilon )n/2$
suffices to force the square of a Hamilton cycle (for some tiny
![]() $\varepsilon \gt 0$
). The next theorem gives such a result. In fact, the result holds for
$\varepsilon \gt 0$
). The next theorem gives such a result. In fact, the result holds for
![]() $k$
th powers of Hamilton cycles more generally, and actually determines the ‘order of magnitude’ of the function between
$k$
th powers of Hamilton cycles more generally, and actually determines the ‘order of magnitude’ of the function between
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $k$
.
$k$
.
Theorem 1.5.
For any
![]() $k\geq 2$
, there exists an
$k\geq 2$
, there exists an
![]() $n_0\in \mathbb N$
such that the following holds for all
$n_0\in \mathbb N$
such that the following holds for all
![]() $n \ge n_0$
. Suppose
$n \ge n_0$
. Suppose
![]() $G$
is an
$G$
is an
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
Then
![]() $G$
contains the
$G$
contains the
![]() $k$
th power of a Hamilton cycle. Furthermore, for every
$k$
th power of a Hamilton cycle. Furthermore, for every
![]() $k\geq 15$
and sufficiently large
$k\geq 15$
and sufficiently large
![]() $n\in \mathbb N$
, there is an
$n\in \mathbb N$
, there is an
![]() $n$
-vertex oriented graph
$n$
-vertex oriented graph
![]() $R_k$
with
$R_k$
with
![]() $\delta ^0(R_k) \gt (\frac {1}{2}-\frac {4}{2^{k/5}})n$
that does not contain the
$\delta ^0(R_k) \gt (\frac {1}{2}-\frac {4}{2^{k/5}})n$
that does not contain the
![]() $k$
th power of a Hamilton cycle.
$k$
th power of a Hamilton cycle.
The furthermore part of Theorem1.5 is proven via Proposition 3.3 in Section 3.2. We suspect that it may be well out of reach to determine (even asymptotically) the minimum semi-degree threshold for forcing the
![]() $k$
th power of a Hamilton cycle. In fact, as indicated above, it has been a challenge to find the ‘right’ candidate for an extremal example even for the
$k$
th power of a Hamilton cycle. In fact, as indicated above, it has been a challenge to find the ‘right’ candidate for an extremal example even for the
![]() $k=2$
case of the problem. Treglown [Reference Treglown35] provided a construction that shows one requires a minimum semi-degree of at least
$k=2$
case of the problem. Treglown [Reference Treglown35] provided a construction that shows one requires a minimum semi-degree of at least
![]() $\delta ^0 (G) \geq 5n/12$
. Later, DeBiasio, cf. [Reference Draganić, Munhá Correia and Sudakov10, Section 1], used a slightly unbalanced blow-up of the Paley tournament on seven vertices to show that
$\delta ^0 (G) \geq 5n/12$
. Later, DeBiasio, cf. [Reference Draganić, Munhá Correia and Sudakov10, Section 1], used a slightly unbalanced blow-up of the Paley tournament on seven vertices to show that
![]() $\delta ^0 (G) \geq 3n/7 -1$
is necessary. We give another example of an oriented graph with large minimum semi-degree and no square of a Hamilton cycle, beating all previous known constructions.
$\delta ^0 (G) \geq 3n/7 -1$
is necessary. We give another example of an oriented graph with large minimum semi-degree and no square of a Hamilton cycle, beating all previous known constructions.
Proposition 1.6.
Given any
![]() $n\in 11\mathbb N$
, there is an
$n\in 11\mathbb N$
, there is an
![]() $n$
-vertex oriented graph
$n$
-vertex oriented graph
![]() $G_2$
with
$G_2$
with
![]() $\delta (G_2)\geq 5n/11-2$
that does not contain the square of a Hamilton cycle.
$\delta (G_2)\geq 5n/11-2$
that does not contain the square of a Hamilton cycle.
The paper is organised as follows. In the next section, we give an overview of the proofs of Theorems1.4 and 1.5. In particular, each of these proofs relies on its own absorbing, connecting, and almost covering lemmas. In Sections 5 and 6, we prove these auxiliary lemmas for Theorems1.4 and 1.5, respectively. Prior to this, in Section 3, we provide the extremal example for Conjecture 1.3 as well as the constructions
![]() $R_k$
and
$R_k$
and
![]() $G_2$
from Theorem1.5 and Proposition 1.6. In Section 4, we introduce some useful tools including Szemerédi’s regularity lemma. The proofs of Theorems1.4 and 1.5 are presented in Section 7. Finally, we give some concluding remarks and results in Section 8. In particular, in Section 8.2, we discuss the Turán problem for oriented graphs.
$G_2$
from Theorem1.5 and Proposition 1.6. In Section 4, we introduce some useful tools including Szemerédi’s regularity lemma. The proofs of Theorems1.4 and 1.5 are presented in Section 7. Finally, we give some concluding remarks and results in Section 8. In particular, in Section 8.2, we discuss the Turán problem for oriented graphs.
Notation. Throughout,
![]() $\mathbb N$
denotes the set of positive integers (i.e. it does not contain
$\mathbb N$
denotes the set of positive integers (i.e. it does not contain
![]() $0$
).
$0$
).
Let
![]() $G$
be a digraph. We define
$G$
be a digraph. We define
![]() $|G| \,:\!= |V(G)|$
and
$|G| \,:\!= |V(G)|$
and
![]() $e(G) \,:\!= |E(G)|$
. Given
$e(G) \,:\!= |E(G)|$
. Given
![]() $x \in V(G)$
, we write
$x \in V(G)$
, we write
![]() $N^+_G(x)$
for the out-neighbourhood of
$N^+_G(x)$
for the out-neighbourhood of
![]() $x$
in
$x$
in
![]() $G$
and write
$G$
and write
![]() $N^-_G(x)$
for the in-neighbourhood of
$N^-_G(x)$
for the in-neighbourhood of
![]() $x$
in
$x$
in
![]() $G$
. Thus,
$G$
. Thus,
![]() $|N^+_G(x)|=d^+_G(x)$
and
$|N^+_G(x)|=d^+_G(x)$
and
![]() $|N^-_G(x)|=d^-_G(x)$
. Given
$|N^-_G(x)|=d^-_G(x)$
. Given
![]() $Y\subseteq V(G)$
we define
$Y\subseteq V(G)$
we define
![]() $N^+_G(x,Y) \,:\!= N^+_G(x) \cap Y$
and
$N^+_G(x,Y) \,:\!= N^+_G(x) \cap Y$
and
![]() $N^-_G(x,Y) \,:\!= N^-_G(x) \cap Y$
. Set
$N^-_G(x,Y) \,:\!= N^-_G(x) \cap Y$
. Set
![]() $d^+_G(x,Y) \,:\!= |N^+_G(x,Y)|$
and
$d^+_G(x,Y) \,:\!= |N^+_G(x,Y)|$
and
![]() $d^-_G(x,Y) \,:\!= |N^-_G(x,Y)|$
, and let
$d^-_G(x,Y) \,:\!= |N^-_G(x,Y)|$
, and let
![]() $d_G(x,Y) \,:\!= d^+_G(x,Y)+ d^-_G(x,Y)$
. We define
$d_G(x,Y) \,:\!= d^+_G(x,Y)+ d^-_G(x,Y)$
. We define
![]() $d_G(x) \,:\!= d_G(x,V(G))$
.
$d_G(x) \,:\!= d_G(x,V(G))$
.
Given two vertices
![]() $x$
and
$x$
and
![]() $y$
of
$y$
of
![]() $G$
, we write
$G$
, we write
![]() $xy$
for the edge directed from
$xy$
for the edge directed from
![]() $x$
to
$x$
to
![]() $y$
. Given subsets
$y$
. Given subsets
![]() $A,B\subseteq V(G)$
(not-necessarily disjoint), let
$A,B\subseteq V(G)$
(not-necessarily disjoint), let
![]() $E_G(A,B)$
(or simply
$E_G(A,B)$
(or simply
![]() $E(A,B)$
) be the set of all
$E(A,B)$
) be the set of all
![]() $xy\in E(G)$
such that
$xy\in E(G)$
such that
![]() $x\in A$
and
$x\in A$
and
![]() $y\in B$
. Let
$y\in B$
. Let
![]() $e_G(A,B) \,:\!= |E(A,B)|$
; we omit the subscript
$e_G(A,B) \,:\!= |E(A,B)|$
; we omit the subscript
![]() $G$
here when the digraph
$G$
here when the digraph
![]() $G$
is clear from the context. Note that
$G$
is clear from the context. Note that
![]() $e_G(A,B)=\sum _{v\in A}d^+_G(v,B)$
.
$e_G(A,B)=\sum _{v\in A}d^+_G(v,B)$
.
If
![]() $A, B\subseteq V(G)$
are disjoint then we define
$A, B\subseteq V(G)$
are disjoint then we define
![]() $G[A,B]$
to be the subdigraph of
$G[A,B]$
to be the subdigraph of
![]() $G$
where
$G$
where
![]() $V(G[A,B])=A \cup B$
and
$V(G[A,B])=A \cup B$
and
![]() $E(G[A\cup B])=E_G(A,B)$
. Given
$E(G[A\cup B])=E_G(A,B)$
. Given
![]() $X \subseteq V(G)$
, we write
$X \subseteq V(G)$
, we write
![]() $G[X]$
for the subdigraph of
$G[X]$
for the subdigraph of
![]() $G$
induced by
$G$
induced by
![]() $X$
. We write
$X$
. We write
![]() $G{\setminus} X$
for the subdigraph of
$G{\setminus} X$
for the subdigraph of
![]() $G$
induced by
$G$
induced by
![]() $V(G){\setminus} X$
.
$V(G){\setminus} X$
.
We write
![]() $C_k$
for the directed cycle on
$C_k$
for the directed cycle on
![]() $k$
vertices. Given a digraph
$k$
vertices. Given a digraph
![]() $G$
, the
$G$
, the
![]() $k$
th power of
$k$
th power of
![]() $G$
is the digraph obtained from
$G$
is the digraph obtained from
![]() $G$
as follows: for each distinct
$G$
as follows: for each distinct
![]() $x,y \in V(G)$
, add the directed edge
$x,y \in V(G)$
, add the directed edge
![]() $xy$
if there is a directed path of length at most
$xy$
if there is a directed path of length at most
![]() $k$
from
$k$
from
![]() $x$
to
$x$
to
![]() $y$
in
$y$
in
![]() $G$
. For brevity we call the
$G$
. For brevity we call the
![]() $k$
th power of a directed path a
$k$
th power of a directed path a
![]() $k$
-path and the
$k$
-path and the
![]() $k$
th power of a directed cycle a
$k$
th power of a directed cycle a
![]() $k$
-cycle. We write
$k$
-cycle. We write
![]() $C^k_{\ell }$
to denote the
$C^k_{\ell }$
to denote the
![]() $k$
-cycle on
$k$
-cycle on
![]() $\ell$
vertices.
$\ell$
vertices.
Given a (di)graph
![]() $G$
and
$G$
and
![]() $t\in \mathbb{N}$
, we let
$t\in \mathbb{N}$
, we let
![]() $G(t)$
denote the
$G(t)$
denote the
![]() $t$
-blow-up of
$t$
-blow-up of
![]() $G$
. More precisely,
$G$
. More precisely,
![]() $V(G(t)) \,:\!= \{v^{j} \colon v \in V(G) \text{ and } j\in [t]\}$
and
$V(G(t)) \,:\!= \{v^{j} \colon v \in V(G) \text{ and } j\in [t]\}$
and
![]() $E(G(t)) \,:\!= \{v^mw^{\ell }\; :\; v w \in E(G) \text{ and }m,\ell \in [t]\}.$
$E(G(t)) \,:\!= \{v^mw^{\ell }\; :\; v w \in E(G) \text{ and }m,\ell \in [t]\}.$
We say that an oriented graph
![]() $G$
is semi-regular if for all
$G$
is semi-regular if for all
![]() $v\in V(G)$
,
$v\in V(G)$
,
![]() $|d^+_G(v)-d^-_G(v)|\leq 1$
.
$|d^+_G(v)-d^-_G(v)|\leq 1$
.
Given (di)graphs
![]() $G$
and
$G$
and
![]() $H$
, an
$H$
, an
![]() $H$
-tiling in
$H$
-tiling in
![]() $G$
is a collection of vertex-disjoint copies of
$G$
is a collection of vertex-disjoint copies of
![]() $H$
in
$H$
in
![]() $G$
. An
$G$
. An
![]() $H$
-factor in
$H$
-factor in
![]() $G$
is a collection of vertex-disjoint copies of
$G$
is a collection of vertex-disjoint copies of
![]() $H$
in
$H$
in
![]() $G$
that together cover
$G$
that together cover
![]() $V(G)$
.
$V(G)$
.
Throughout the paper, we omit all floor and ceiling signs whenever these are not crucial. The constants in the hierarchies used to state our results are chosen from right to left. For example, if we claim that a result holds whenever
![]() $0\lt a\ll b\ll c\le 1$
, then there are non-decreasing functions
$0\lt a\ll b\ll c\le 1$
, then there are non-decreasing functions
![]() $f\; :\; (0,1]\to (0,1]$
and
$f\; :\; (0,1]\to (0,1]$
and
![]() $g\; :\; (0,1]\to (0,1]$
such that the result holds for all
$g\; :\; (0,1]\to (0,1]$
such that the result holds for all
![]() $0\lt a,b,c\le 1$
with
$0\lt a,b,c\le 1$
with
![]() $b\le f(c)$
and
$b\le f(c)$
and
![]() $a\le g(b)$
. Note that
$a\le g(b)$
. Note that
![]() $a \ll b$
implies that we may assume in the proof that, for example,
$a \ll b$
implies that we may assume in the proof that, for example,
![]() $a \lt b$
or
$a \lt b$
or
![]() $a \lt b^2$
.
$a \lt b^2$
.
2. Overview of the proofs of Theorems1.4 and 1.5
The proofs of both Theorems1.4 and 1.5 are similar and follow the same high-level strategy, though the details in each case are different. In particular, for both, we use the connecting–absorbing method, a technique first developed by Rödl, Ruciński, and Szemerédi [Reference Rödl, Ruciński and Szemerédi32]. Suppose one wishes to embed the
![]() $k$
th power of a Hamilton cycle in an
$k$
th power of a Hamilton cycle in an
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
, and let
$G$
, and let
![]() $0\lt \varepsilon \ll \eta \ll 1$
. Then, roughly speaking, an application of this method consists of three main steps:
$0\lt \varepsilon \ll \eta \ll 1$
. Then, roughly speaking, an application of this method consists of three main steps:
-
• Step 1, the absorbing
 $k$
-path
$k$
-path
 $P_A$
. Find a
$P_A$
. Find a
 $k$
-path
$k$
-path
 $P_A$
in
$P_A$
in
 $G$
such that
$G$
such that
 $|P_A|\leq \eta n$
. The
$|P_A|\leq \eta n$
. The
 $k$
-path
$k$
-path
 $P_A$
has the property that given any set
$P_A$
has the property that given any set
 $L \subseteq V(G) {\setminus} V(P_A)$
such that
$L \subseteq V(G) {\setminus} V(P_A)$
such that
 $|L|\leq 2 \varepsilon n$
,
$|L|\leq 2 \varepsilon n$
,
 $G$
contains a
$G$
contains a
 $k$
-path
$k$
-path
 $P$
with vertex set
$P$
with vertex set
 $V(P_A) \cup L$
, where the first
$V(P_A) \cup L$
, where the first
 $k$
vertices on
$k$
vertices on
 $P$
are the same as the first
$P$
are the same as the first
 $k$
vertices on
$k$
vertices on
 $P_A$
; similarly, the last
$P_A$
; similarly, the last
 $k$
vertices on
$k$
vertices on
 $P$
are the same as the last
$P$
are the same as the last
 $k$
vertices on
$k$
vertices on
 $P_A$
.
$P_A$
. -
• Step 2, the reservoir set
 $\mathfrak R$
. Let
$\mathfrak R$
. Let
 $G' \,:\!= G{\setminus} V(P_A)$
. Find a set
$G' \,:\!= G{\setminus} V(P_A)$
. Find a set
 $\mathfrak R \subseteq V(G')$
such that
$\mathfrak R \subseteq V(G')$
such that
 $|\mathfrak R|\leq \varepsilon n$
and so that
$|\mathfrak R|\leq \varepsilon n$
and so that
 $\mathfrak R$
has the following property: given arbitrary disjoint ordered
$\mathfrak R$
has the following property: given arbitrary disjoint ordered
 $k$
-sets
$k$
-sets
 $X,Y \subseteq V(G)$
, there are many short
$X,Y \subseteq V(G)$
, there are many short
 $k$
-paths
$k$
-paths
 $P$
in
$P$
in
 $G$
so that the first
$G$
so that the first
 $k$
vertices on
$k$
vertices on
 $P$
are the elements of
$P$
are the elements of
 $X$
, ordered as in
$X$
, ordered as in
 $X$
; the last
$X$
; the last
 $k$
vertices on
$k$
vertices on
 $P$
are the elements of
$P$
are the elements of
 $Y$
, ordered as in
$Y$
, ordered as in
 $Y$
; and
$Y$
; and
 $V(P){\setminus} (X \cup Y) \subseteq \mathfrak R$
.
$V(P){\setminus} (X \cup Y) \subseteq \mathfrak R$
. -
• Step 3, almost covering with
 $k$
-paths. Let
$k$
-paths. Let
 $G'' \,:\!= G'{\setminus} \mathfrak R$
. Find a collection
$G'' \,:\!= G'{\setminus} \mathfrak R$
. Find a collection
 $\mathcal P$
of a bounded number of vertex-disjoint
$\mathcal P$
of a bounded number of vertex-disjoint
 $k$
-paths in
$k$
-paths in
 $G''$
that together cover all but at most
$G''$
that together cover all but at most
 $\varepsilon n$
of the vertices in
$\varepsilon n$
of the vertices in
 $G''$
.
$G''$
.
These three steps then yield the
![]() $k$
th power of a Hamilton cycle in
$k$
th power of a Hamilton cycle in
![]() $G$
. Indeed, one can use the reservoir set
$G$
. Indeed, one can use the reservoir set
![]() $\mathfrak R$
to connect together all of the
$\mathfrak R$
to connect together all of the
![]() $k$
-paths in
$k$
-paths in
![]() $\mathcal P$
and
$\mathcal P$
and
![]() $P_A$
into a single
$P_A$
into a single
![]() $k$
-cycle
$k$
-cycle
![]() $C^k$
in
$C^k$
in
![]() $G$
that covers all but at most
$G$
that covers all but at most
![]() $\varepsilon n$
of the vertices from
$\varepsilon n$
of the vertices from
![]() $G''$
and some of the vertices from
$G''$
and some of the vertices from
![]() $\mathfrak R$
. In total at most
$\mathfrak R$
. In total at most
![]() $2\varepsilon n$
vertices in
$2\varepsilon n$
vertices in
![]() $G$
are not covered by
$G$
are not covered by
![]() $C^k$
; these can then be absorbed by
$C^k$
; these can then be absorbed by
![]() $P_A$
to obtain the
$P_A$
to obtain the
![]() $k$
th power of a Hamilton cycle in
$k$
th power of a Hamilton cycle in
![]() $G$
.
$G$
.
As mentioned earlier, the proofs of Theorems1.4 and 1.5 each rely on their own absorbing, connecting and almost covering lemmas. The almost covering lemmas are used to complete Step 3. Roughly speaking, the connecting lemmas ensure that for any disjoint ordered
![]() $k$
-sets
$k$
-sets
![]() $X,Y \subseteq V(G)$
we can find many short
$X,Y \subseteq V(G)$
we can find many short
![]() $k$
-paths
$k$
-paths
![]() $P$
in
$P$
in
![]() $G$
so that the first
$G$
so that the first
![]() $k$
vertices on
$k$
vertices on
![]() $P$
are the elements of
$P$
are the elements of
![]() $X$
, ordered as in
$X$
, ordered as in
![]() $X$
, and the last
$X$
, and the last
![]() $k$
vertices on
$k$
vertices on
![]() $P$
are the elements of
$P$
are the elements of
![]() $Y$
, ordered as in
$Y$
, ordered as in
![]() $Y$
. These connecting lemmas are then used to construct the reservoir in Step 2.
$Y$
. These connecting lemmas are then used to construct the reservoir in Step 2.
In fact, the connecting lemmas are also used in Step 1. Indeed, the absorbing lemmas establish that for every vertex
![]() $v \in V(G)$
, there are many short
$v \in V(G)$
, there are many short
![]() $k$
-paths
$k$
-paths
![]() $P_v$
in
$P_v$
in
![]() $G$
with the property that one can insert
$G$
with the property that one can insert
![]() $v$
into the middle of
$v$
into the middle of
![]() $P_v$
so that the resulting digraph is still a
$P_v$
so that the resulting digraph is still a
![]() $k$
-path. By randomly sampling amongst all such
$k$
-path. By randomly sampling amongst all such
![]() $k$
-paths
$k$
-paths
![]() $P_v$
(for all
$P_v$
(for all
![]() $v \in V(G)$
), and then joining the selected
$v \in V(G)$
), and then joining the selected
![]() $k$
-paths up via the connecting lemma, one can obtain the absorbing
$k$
-paths up via the connecting lemma, one can obtain the absorbing
![]() $k$
-path
$k$
-path
![]() $P_A$
from Step 1.
$P_A$
from Step 1.
In the case of Theorem1.5, things are a little more subtle than we have indicated above. Indeed, we cannot actually achieve Step 2 for arbitrary ordered
![]() $k$
-sets
$k$
-sets
![]() $X,Y \subseteq V(G)$
since there may be a choice of
$X,Y \subseteq V(G)$
since there may be a choice of
![]() $X$
and
$X$
and
![]() $Y$
for which the vertices in
$Y$
for which the vertices in
![]() $X$
do not even have a single common out-neighbour (or the vertices in
$X$
do not even have a single common out-neighbour (or the vertices in
![]() $Y$
do not have a common in-neighbour). Thus, we need to argue more carefully to ensure we only ever connect between ‘well-behaved’
$Y$
do not have a common in-neighbour). Thus, we need to argue more carefully to ensure we only ever connect between ‘well-behaved’
![]() $X,Y \subseteq V(G)$
.
$X,Y \subseteq V(G)$
.
By applying two results from [Reference Czygrinow, DeBiasio, Molla and Treglown8], the proofs of the absorbing and almost covering lemmas for Theorem1.4 are not too difficult. The main work for this theorem is proving the connecting lemma. The proof of Theorem1.5 is a little more involved. In the proofs of the absorbing and connecting lemmas, we make use of the method of dependent random choice. The proof of the almost covering lemma is quite non-standard, and we apply the aforementioned result of Draganić, Munhá Correia, and Sudakov [Reference Draganić, Munhá Correia and Sudakov10] on powers of Hamilton cycles in tournaments of large minimum semi-degree.
3. The extremal examples
3.1 The extremal example for Conjecture 1.3
The following provides an extremal construction
![]() $G$
for Conjecture 1.3.
$G$
for Conjecture 1.3.
Proposition 3.1.
Let
![]() $k,q\in \mathbb N$
and
$k,q\in \mathbb N$
and
![]() $r\in \mathbb Z$
such that
$r\in \mathbb Z$
such that
![]() $n=(k+3)q+r$
where
$n=(k+3)q+r$
where
![]() $0\leq r\leq k+2$
. There exists an
$0\leq r\leq k+2$
. There exists an
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with
$G$
with
 \begin{equation*}\delta (G)= \begin{cases} 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -4 & \textit{ if } r=k+2, \\[7pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -3 & \textit{ if } r = k \textit{ or } r=k+1 , \\[7pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -2 & \textit{ otherwise,}\end{cases} \end{equation*}
\begin{equation*}\delta (G)= \begin{cases} 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -4 & \textit{ if } r=k+2, \\[7pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -3 & \textit{ if } r = k \textit{ or } r=k+1 , \\[7pt] 2\left\lceil \left(1-\frac {1}{k+3}\right)n\right\rceil -2 & \textit{ otherwise,}\end{cases} \end{equation*}
that does not contain the
![]() $k$
th power of a Hamilton cycle.
$k$
th power of a Hamilton cycle.
Proof. Let
![]() $k,q\in \mathbb N$
and
$k,q\in \mathbb N$
and
![]() $r\in \mathbb Z$
such that
$r\in \mathbb Z$
such that
![]() $n=(k+3)q+r$
, where
$n=(k+3)q+r$
, where
![]() $0\leq r\leq k+2$
. Define integers
$0\leq r\leq k+2$
. Define integers
![]() $r_1,\ldots , r_{k+1}$
as equally as possible so that
$r_1,\ldots , r_{k+1}$
as equally as possible so that
![]() $2 \geq r_1 \geq r_2 \geq \ldots \geq r_{k+1} \geq 0$
and
$2 \geq r_1 \geq r_2 \geq \ldots \geq r_{k+1} \geq 0$
and
![]() $r=\sum _{i=1}^{k+1}r_i$
.
$r=\sum _{i=1}^{k+1}r_i$
.
Let
![]() $G$
be the
$G$
be the
![]() $n$
-vertex digraph consisting of
$n$
-vertex digraph consisting of
![]() $k-1$
independent sets
$k-1$
independent sets
![]() $V_1,\ldots , V_{k-1}$
and two other classes
$V_1,\ldots , V_{k-1}$
and two other classes
![]() $V_k$
and
$V_k$
and
![]() $V_{k+1}$
so that there are all possible double edges going out of the
$V_{k+1}$
so that there are all possible double edges going out of the
![]() $k-1$
independent sets; all possible double edges inside of
$k-1$
independent sets; all possible double edges inside of
![]() $V_{k}$
and inside of
$V_{k}$
and inside of
![]() $V_{k+1}$
; all possible directed edges from
$V_{k+1}$
; all possible directed edges from
![]() $V_k$
to
$V_k$
to
![]() $V_{k+1}$
(but none from
$V_{k+1}$
(but none from
![]() $V_{k+1}$
to
$V_{k+1}$
to
![]() $V_k$
). Moreover, we choose the classes so that
$V_k$
). Moreover, we choose the classes so that
![]() $|V_i|=q+r_i$
for all
$|V_i|=q+r_i$
for all
![]() $i \in [k-1]$
, and
$i \in [k-1]$
, and
![]() $|V_i|=2q+r_i$
for all
$|V_i|=2q+r_i$
for all
![]() $i \in \{k,k+1\}$
.
$i \in \{k,k+1\}$
.
Let
![]() $v\in V_i$
. If
$v\in V_i$
. If
![]() $i\in [k-1]$
, then
$i\in [k-1]$
, then
![]() $d_G(v)=2((k+2)q+r)-2r_i=2\lceil (1-\frac {1}{k+3})n\rceil -2r_i$
. If
$d_G(v)=2((k+2)q+r)-2r_i=2\lceil (1-\frac {1}{k+3})n\rceil -2r_i$
. If
![]() $i\in \{k,k+1\}$
, then
$i\in \{k,k+1\}$
, then
![]() $d_G(v)=2((k+2)q+r)-r_j-2=2\lceil (1-\frac {1}{k+3})n\rceil -r_j-2$
where
$d_G(v)=2((k+2)q+r)-r_j-2=2\lceil (1-\frac {1}{k+3})n\rceil -r_j-2$
where
![]() $j\! \in\! \{k,k+1\} {\setminus} \{i\}$
. Therefore,
$j\! \in\! \{k,k+1\} {\setminus} \{i\}$
. Therefore,
![]() $\delta (G)$
is as in the statement of the proposition.
$\delta (G)$
is as in the statement of the proposition.
Suppose for a contradiction that there is a
![]() $k$
th power of a Hamilton cycle
$k$
th power of a Hamilton cycle
![]() $C$
in
$C$
in
![]() $G$
. Notice that every transitive tournament on
$G$
. Notice that every transitive tournament on
![]() $k+1$
vertices in
$k+1$
vertices in
![]() $G$
contains at least two vertices from
$G$
contains at least two vertices from
![]() $V_k \cup V_{k+1}$
. By following the same ordering of vertices in
$V_k \cup V_{k+1}$
. By following the same ordering of vertices in
![]() $V_k \cup V_{k+1}$
appearing in
$V_k \cup V_{k+1}$
appearing in
![]() $C$
, we deduce that
$C$
, we deduce that
![]() $C[V_k \cup V_{k+1}]$
, and therefore
$C[V_k \cup V_{k+1}]$
, and therefore
![]() $ G[V_k \cup V_{k+1}]$
, contains a Hamilton cycle. However,
$ G[V_k \cup V_{k+1}]$
, contains a Hamilton cycle. However,
![]() $G[V_k \cup V_{k+1}]$
is not strongly connected, a contradiction.
$G[V_k \cup V_{k+1}]$
is not strongly connected, a contradiction.
3.2 The extremal example for Theorem1.5
Let
![]() $\vec {T}_k$
be the transitive tournament on
$\vec {T}_k$
be the transitive tournament on
![]() $k$
vertices and let
$k$
vertices and let
![]() $\vec {r}(k)$
be the smallest
$\vec {r}(k)$
be the smallest
![]() $n\in {\mathbb{N}}$
such that every
$n\in {\mathbb{N}}$
such that every
![]() $n$
-vertex tournament contains a copy of
$n$
-vertex tournament contains a copy of
![]() $\vec {T}_k$
. Let
$\vec {T}_k$
. Let
![]() $\vec {tr}(k)$
be the smallest
$\vec {tr}(k)$
be the smallest
![]() $n\in k{\mathbb{N}}$
such that every
$n\in k{\mathbb{N}}$
such that every
![]() $n$
-vertex tournament has a
$n$
-vertex tournament has a
![]() $\vec {T}_k$
-factor.
$\vec {T}_k$
-factor.

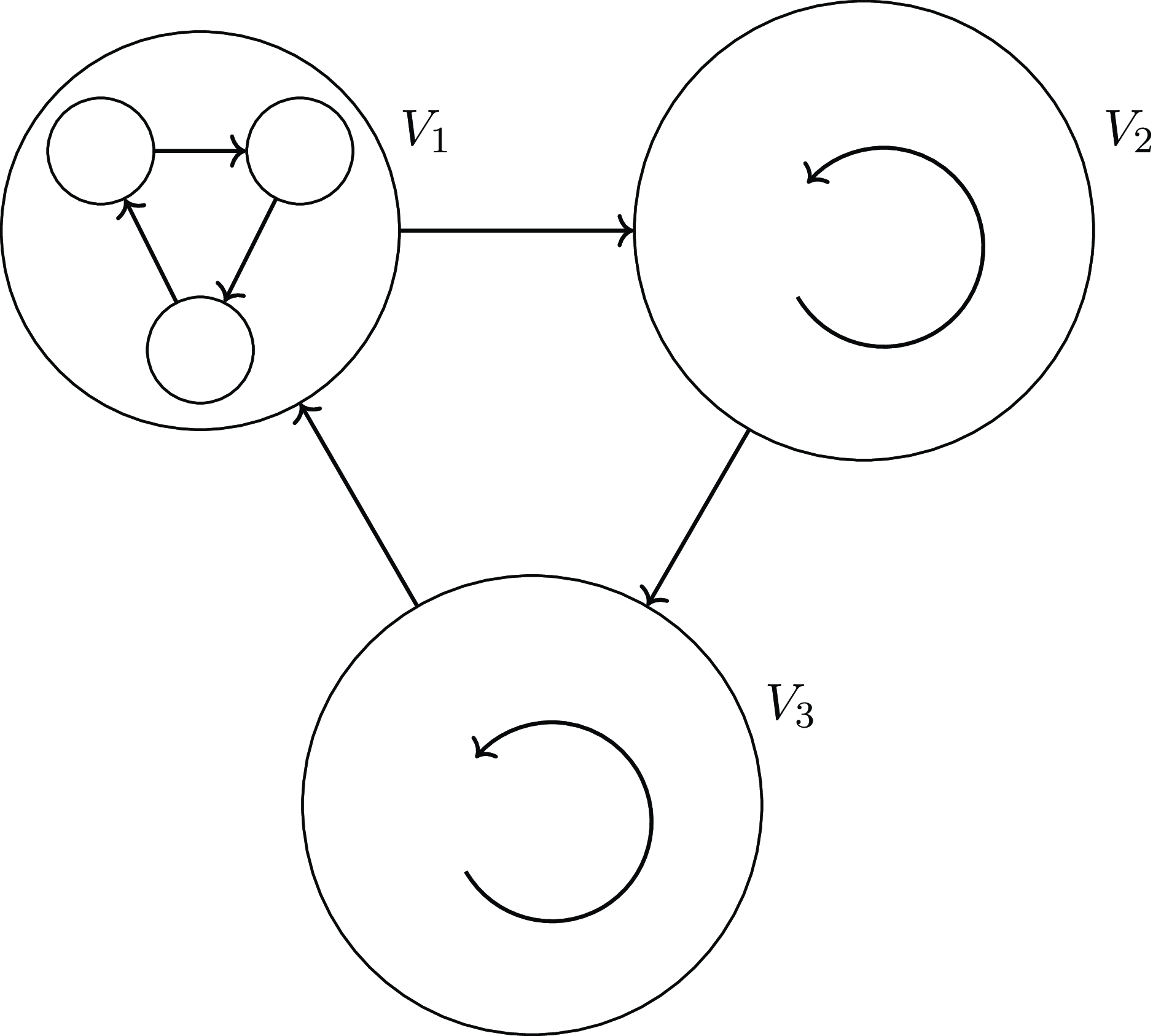
Figure 1. The oriented graph
![]() $G_{2}$
does not contain a square of Hamilton cycle.
$G_{2}$
does not contain a square of Hamilton cycle.
It is known that
![]() $\vec {r}(3)=4$
,
$\vec {r}(3)=4$
,
![]() $\vec {r}(4)=8$
,
$\vec {r}(4)=8$
,
![]() $\vec {r}(5)=14$
,
$\vec {r}(5)=14$
,
![]() $\vec {r}(6)=28$
, and
$\vec {r}(6)=28$
, and
![]() $\lfloor \sqrt {2}^{k-1} \rfloor \lt \vec {r}(k) \le 2^{k-1}$
. Also
$\lfloor \sqrt {2}^{k-1} \rfloor \lt \vec {r}(k) \le 2^{k-1}$
. Also
![]() $\vec {tr}(3)=6$
,
$\vec {tr}(3)=6$
,
![]() $\vec {tr}(4)=16$
, and
$\vec {tr}(4)=16$
, and
![]() $ \vec {r}(k)\leq \vec {tr}(k)\lt 4^k$
(see [Reference Bucić and Sudakov6, Section 5] for a comment about an improvement to this upper bound). We highlight that in all examples where
$ \vec {r}(k)\leq \vec {tr}(k)\lt 4^k$
(see [Reference Bucić and Sudakov6, Section 5] for a comment about an improvement to this upper bound). We highlight that in all examples where
![]() $\vec {r}(k+1)$
is known, the lower bound example is a regular tournament. In particular, this is used in the proof of the following result.
$\vec {r}(k+1)$
is known, the lower bound example is a regular tournament. In particular, this is used in the proof of the following result.
Proposition 3.2.
Let
![]() $2 \leq k \le 5$
. Given any
$2 \leq k \le 5$
. Given any
![]() $n \in \mathbb N$
divisible by
$n \in \mathbb N$
divisible by
![]() $3\vec {r}(k+1)-1$
, there exists an
$3\vec {r}(k+1)-1$
, there exists an
![]() $n$
-vertex oriented graph
$n$
-vertex oriented graph
![]() $G_k$
with
$G_k$
with
that does not contain the
![]() $k$
th power of a Hamilton cycle.
$k$
th power of a Hamilton cycle.
Proof. Set
![]() $m \,:\!= \vec {r}(k+1)-1$
and let
$m \,:\!= \vec {r}(k+1)-1$
and let
![]() $n=(3m+2)t$
for some
$n=(3m+2)t$
for some
![]() $t \in \mathbb N$
. Consider the
$t \in \mathbb N$
. Consider the
![]() $n$
-vertex oriented graph
$n$
-vertex oriented graph
![]() $G_k$
defined as follows (see also Figure 1 for
$G_k$
defined as follows (see also Figure 1 for
![]() $k=2$
). The vertex set of
$k=2$
). The vertex set of
![]() $G_{k}$
consists of sets
$G_{k}$
consists of sets
![]() $V_1, V_2, V_3$
where either (i)
$V_1, V_2, V_3$
where either (i)
![]() $|V_1|= m t$
and
$|V_1|= m t$
and
![]() $|V_2|=|V_3|=(m+1)t$
or (ii)
$|V_2|=|V_3|=(m+1)t$
or (ii)
![]() $|V_1|= m t -1$
,
$|V_1|= m t -1$
,
![]() $|V_2|=(m+1)t+1$
and
$|V_2|=(m+1)t+1$
and
![]() $|V_3|=(m+1)t$
. We choose the sizes of the
$|V_3|=(m+1)t$
. We choose the sizes of the
![]() $V_i$
such that
$V_i$
such that
![]() $|V_1|$
is not divisible by
$|V_1|$
is not divisible by
![]() $k$
. Add all edges directed from
$k$
. Add all edges directed from
![]() $V_1$
to
$V_1$
to
![]() $V_{2}$
, from
$V_{2}$
, from
![]() $V_2$
to
$V_2$
to
![]() $V_{3}$
, and from
$V_{3}$
, and from
![]() $V_3$
to
$V_3$
to
![]() $V_{1}$
. Both
$V_{1}$
. Both
![]() $G_k[V_2]$
and
$G_k[V_2]$
and
![]() $G_k[V_3]$
are semi-regular tournaments. Finally, let
$G_k[V_3]$
are semi-regular tournaments. Finally, let
![]() $G_k[V_1]$
be the
$G_k[V_1]$
be the
![]() $t$
-blow-up of the regular tournament on
$t$
-blow-up of the regular tournament on
![]() $m$
vertices that contains no copy of
$m$
vertices that contains no copy of
![]() $\vec {T}_{k+1}$
(where one vertex is deleted if
$\vec {T}_{k+1}$
(where one vertex is deleted if
![]() $|V_1|=mt-1$
). It is easy to check that the desired minimum semi-degree condition holds.
$|V_1|=mt-1$
). It is easy to check that the desired minimum semi-degree condition holds.
Consider any
![]() $k$
th power of a cycle
$k$
th power of a cycle
![]() $C$
in
$C$
in
![]() $G_k$
. Notice that any copy of
$G_k$
. Notice that any copy of
![]() $\vec {T}_{k+1}$
in
$\vec {T}_{k+1}$
in
![]() $G_k$
must contain vertices from at most two of the classes
$G_k$
must contain vertices from at most two of the classes
![]() $V_1$
,
$V_1$
,
![]() $V_2$
, and
$V_2$
, and
![]() $V_3$
. This implies that every time
$V_3$
. This implies that every time
![]() $C$
enters
$C$
enters
![]() $V_1$
(from
$V_1$
(from
![]() $V_3$
), it must traverse at least
$V_3$
), it must traverse at least
![]() $k$
vertices before leaving
$k$
vertices before leaving
![]() $V_1$
(and entering
$V_1$
(and entering
![]() $V_2$
). In fact, since
$V_2$
). In fact, since
![]() $G_k[V_1]$
does not contain a copy of
$G_k[V_1]$
does not contain a copy of
![]() $\vec {T}_{k+1}$
, precisely
$\vec {T}_{k+1}$
, precisely
![]() $k$
vertices in
$k$
vertices in
![]() $V_1$
are covered in each such step. Thus, the number of vertices in
$V_1$
are covered in each such step. Thus, the number of vertices in
![]() $V_1$
covered by
$V_1$
covered by
![]() $C$
is a multiple of
$C$
is a multiple of
![]() $k$
. Therefore,
$k$
. Therefore,
![]() $C$
cannot contain all of
$C$
cannot contain all of
![]() $V_1$
since
$V_1$
since
![]() $|V_1|$
is not divisible by
$|V_1|$
is not divisible by
![]() $k$
.
$k$
.
Note that Proposition 3.2 immediately implies Proposition 1.6.
Next, we prove the following general result, which immediately yields the furthermore part of Theorem1.5. We will make use of the probabilistic construction of Erdős and Moser [Reference Erdős and Moser13] (which proves that
![]() $\vec {r}(k+1)\gt \lfloor \sqrt {2}^k\rfloor$
), combined with an additional calculation to show that a random tournament on
$\vec {r}(k+1)\gt \lfloor \sqrt {2}^k\rfloor$
), combined with an additional calculation to show that a random tournament on
![]() $T$
vertices has minimum semi-degree very close to
$T$
vertices has minimum semi-degree very close to
![]() $T/2$
.
$T/2$
.
Proposition 3.3.
For every
![]() $k\geq 15$
and sufficiently large
$k\geq 15$
and sufficiently large
![]() $n\in \mathbb N$
, there is an
$n\in \mathbb N$
, there is an
![]() $n$
-vertex oriented graph
$n$
-vertex oriented graph
![]() $R_k$
with
$R_k$
with
that does not contain a copy of
![]() $\vec T_{k+1}$
and thus a
$\vec T_{k+1}$
and thus a
![]() $k$
th power of a Hamilton cycle.
$k$
th power of a Hamilton cycle.
Proof. Let
![]() $k\geq 15$
and set
$k\geq 15$
and set
![]() $t \,:\!= \lceil 2^{(k-5)/2}\rceil$
. We first shall prove that there is a (randomly generated)
$t \,:\!= \lceil 2^{(k-5)/2}\rceil$
. We first shall prove that there is a (randomly generated)
![]() $t$
-vertex tournament
$t$
-vertex tournament
![]() $T(k)$
with
$T(k)$
with
![]() $\delta ^0(T(k)) \geq \big (\frac {1}{2}-\frac {3/2}{t^{2/5}}-\frac {1}{2t}\big )t$
that is
$\delta ^0(T(k)) \geq \big (\frac {1}{2}-\frac {3/2}{t^{2/5}}-\frac {1}{2t}\big )t$
that is
![]() $\vec {T}_{k+1}$
-free. Then we will get the desired oriented graph by taking a blow-up of such a tournament.
$\vec {T}_{k+1}$
-free. Then we will get the desired oriented graph by taking a blow-up of such a tournament.
Consider a random tournament
![]() $T$
on
$T$
on
![]() $t$
vertices; that is, the orientation of each edge is selected uniformly at random, independently of all other edges. By the union bound,
$t$
vertices; that is, the orientation of each edge is selected uniformly at random, independently of all other edges. By the union bound,
By Chernoff’s bound,Footnote
3
for each
![]() $v \in V(T)$
, we have
$v \in V(T)$
, we have
Then, by the union bound, we have
Thus, the probability that one of the events (3.1) or (3.2) holds is at most
where the inequality holds for all
![]() $k\geq 15$
(in fact, one can see that the inequality holds for all
$k\geq 15$
(in fact, one can see that the inequality holds for all
![]() $k\geq 2$
, but we are assuming
$k\geq 2$
, but we are assuming
![]() $k\geq 15$
in this context). Hence, there is a tournament
$k\geq 15$
in this context). Hence, there is a tournament
![]() $T(k)$
on
$T(k)$
on
![]() $t$
vertices with
$t$
vertices with
![]() $\delta ^0(T(k))\gt \big (\frac {1}{2} - \frac {3/2}{t^{2/5}}-\frac {1}{2t}\big )t$
not containing a copy of
$\delta ^0(T(k))\gt \big (\frac {1}{2} - \frac {3/2}{t^{2/5}}-\frac {1}{2t}\big )t$
not containing a copy of
![]() $\vec T_{k+1}$
.
$\vec T_{k+1}$
.
Finally,
![]() $R_k$
is obtained by blowing up each vertex of
$R_k$
is obtained by blowing up each vertex of
![]() $T(k)$
into a set of size
$T(k)$
into a set of size
![]() $\lfloor \frac {n}{t}\rfloor$
or
$\lfloor \frac {n}{t}\rfloor$
or
![]() $\lceil \frac {n}{t}\rceil$
so that it contains
$\lceil \frac {n}{t}\rceil$
so that it contains
![]() $n$
vertices in total. Thus,
$n$
vertices in total. Thus,
![]() $R_k$
does not contain a copy of
$R_k$
does not contain a copy of
![]() $\vec {T}_{k+1}$
and
$\vec {T}_{k+1}$
and
 \begin{align*}\delta ^0(R_k)\gt \bigg (\frac {1}{2}-\frac {3/2}{t^{2/5}}-\frac {1}{2t}\bigg )t\cdot \left \lfloor \frac {n}{t}\right \rfloor \geq \bigg (\frac {1}{2}-\frac {3/2}{t^{2/5}}-\frac {1}{2t}\bigg )(n-(t-1)) & \geq \bigg (\frac {1}{2}-\frac {2}{t^{2/5}}\bigg )n \\& \geq \bigg (\frac {1}{2}-\frac {4}{2^{k/5}}\bigg )n ,\end{align*}
\begin{align*}\delta ^0(R_k)\gt \bigg (\frac {1}{2}-\frac {3/2}{t^{2/5}}-\frac {1}{2t}\bigg )t\cdot \left \lfloor \frac {n}{t}\right \rfloor \geq \bigg (\frac {1}{2}-\frac {3/2}{t^{2/5}}-\frac {1}{2t}\bigg )(n-(t-1)) & \geq \bigg (\frac {1}{2}-\frac {2}{t^{2/5}}\bigg )n \\& \geq \bigg (\frac {1}{2}-\frac {4}{2^{k/5}}\bigg )n ,\end{align*}
as desired (where we used the fact that
![]() $n$
is sufficiently large in the second to last inequality and the fact that
$n$
is sufficiently large in the second to last inequality and the fact that
![]() $t=\lceil 2^{(k-5)/2}\rceil \geq 2^{(k-5)/2}$
in the last inequality).
$t=\lceil 2^{(k-5)/2}\rceil \geq 2^{(k-5)/2}$
in the last inequality).
While Proposition 3.3 is sufficient for our purposes, one can adapt the proof of Proposition 3.2 to obtain an oriented graph
![]() $R_k'$
which does not contain the
$R_k'$
which does not contain the
![]() $k$
th power of a Hamilton cycle and has a higher minimum semi-degree. Indeed, one can adapt the construction in Proposition 3.2 so that now
$k$
th power of a Hamilton cycle and has a higher minimum semi-degree. Indeed, one can adapt the construction in Proposition 3.2 so that now
![]() $V_1$
is spanned by the blow-up of a random tournament. However, to obtain a better understanding of the minimum semi-degree threshold, one would likely need a deeper understanding of the function
$V_1$
is spanned by the blow-up of a random tournament. However, to obtain a better understanding of the minimum semi-degree threshold, one would likely need a deeper understanding of the function
![]() $\vec r(k)$
.
$\vec r(k)$
.
4. The regularity lemma and related results
The diregularity lemma is a version of the regularity lemma for digraphs proved by Alon and Shapira [Reference Alon and Shapira2]. In this section we discuss the diregularity lemma and other related results that are needed for our proofs.
We first require some notation. Let
![]() $G$
be a digraph and
$G$
be a digraph and
![]() $A,B\subseteq V(G)$
be disjoint. The density of
$A,B\subseteq V(G)$
be disjoint. The density of
![]() $(A,B)$
is defined by
$(A,B)$
is defined by
![]() $d_G(A,B) \,:\!= \tfrac {e_G(A,B)}{|A||B|}$
. We will write
$d_G(A,B) \,:\!= \tfrac {e_G(A,B)}{|A||B|}$
. We will write
![]() $d(A,B)$
if this is unambiguous. Note that
$d(A,B)$
if this is unambiguous. Note that
![]() $d(A,B)$
is not necessarily equal to
$d(A,B)$
is not necessarily equal to
![]() $d(B,A)$
. Given
$d(B,A)$
. Given
![]() $\varepsilon \gt 0$
, we say that
$\varepsilon \gt 0$
, we say that
![]() $(A,B)$
is
$(A,B)$
is
![]() $\varepsilon$
-regular (in
$\varepsilon$
-regular (in
![]() $G$
) if for all subsets
$G$
) if for all subsets
![]() $A'\subseteq A$
and
$A'\subseteq A$
and
![]() $B' \subseteq B$
with
$B' \subseteq B$
with
![]() $|A'|\gt \varepsilon |A|$
and
$|A'|\gt \varepsilon |A|$
and
![]() $|B'|\gt \varepsilon |B|$
, we have
$|B'|\gt \varepsilon |B|$
, we have
Finally, if
![]() $G=G[A, B]$
, we write
$G=G[A, B]$
, we write
![]() $G=(A,B)$
.
$G=(A,B)$
.
We now state the degree form of the diregularity lemma.
Lemma 4.1 (Diregularity lemma [Reference Alon and Shapira2]). Given any
![]() $\varepsilon \in (0,1)$
and
$\varepsilon \in (0,1)$
and
![]() $t_0\in \mathbb N$
, there exist
$t_0\in \mathbb N$
, there exist
![]() $T=T(\varepsilon ,t_0) \in \mathbb N$
and
$T=T(\varepsilon ,t_0) \in \mathbb N$
and
![]() $n_0=n_0(\varepsilon , t_0)\in \mathbb N$
such that the following holds for all
$n_0=n_0(\varepsilon , t_0)\in \mathbb N$
such that the following holds for all
![]() $n \geq n_0$
. Let
$n \geq n_0$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex digraph and let
$n$
-vertex digraph and let
![]() $d\in [0,1]$
. Then, there is a partition
$d\in [0,1]$
. Then, there is a partition
![]() $\{V_0, V_1,\ldots , V_t\}$
of
$\{V_0, V_1,\ldots , V_t\}$
of
![]() $V(G)$
with
$V(G)$
with
![]() $t_0\lt t\lt T$
and a spanning subdigraph
$t_0\lt t\lt T$
and a spanning subdigraph
![]() $G'$
of
$G'$
of
![]() $ G$
such that
$ G$
such that
-
(a)
 $|V_0|\leq \varepsilon n$
;
$|V_0|\leq \varepsilon n$
; -
(b)
 $|V_i|=|V_1|$
for every
$|V_i|=|V_1|$
for every
 $i\in [t]$
;
$i\in [t]$
; -
(c) for every
 $v \in V(G)$
,
$v \in V(G)$
,
 $d^{+}_{G'}(v)\gt d^{+}_G(v)-(d+\varepsilon )n$
and
$d^{+}_{G'}(v)\gt d^{+}_G(v)-(d+\varepsilon )n$
and
 $d^{-}_{G'}(v)\gt d^{-}_G(v)-(d+\varepsilon )n$
;
$d^{-}_{G'}(v)\gt d^{-}_G(v)-(d+\varepsilon )n$
; -
(d)
 $e(G'[V_i])=0$
for every
$e(G'[V_i])=0$
for every
 $i\in [t]$
;
$i\in [t]$
; -
(e) for every distinct
 $i,j\in [t]$
, the pair
$i,j\in [t]$
, the pair
 $(V_i,V_j)$
is
$(V_i,V_j)$
is
 $\varepsilon$
-regular in
$\varepsilon$
-regular in
 $G'$
with density either
$G'$
with density either
 $0$
or at least
$0$
or at least
 $d$
.
$d$
.
We call
![]() $V_1,\ldots , V_k$
clusters,
$V_1,\ldots , V_k$
clusters,
![]() $V_0$
the exceptional set and the vertices in
$V_0$
the exceptional set and the vertices in
![]() $V_0$
exceptional vertices. We refer to
$V_0$
exceptional vertices. We refer to
![]() $G_0$
as the pure digraph. The last condition of Lemma 4.1 says that all pairs of clusters are
$G_0$
as the pure digraph. The last condition of Lemma 4.1 says that all pairs of clusters are
![]() $\varepsilon$
-regular in both directions, but possibly with different densities. The reduced digraph
$\varepsilon$
-regular in both directions, but possibly with different densities. The reduced digraph
![]() $R$
of
$R$
of
![]() $G$
with parameters
$G$
with parameters
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
is the digraph defined by
$t_0$
is the digraph defined by
The following well-known result states that the reduced digraph of
![]() $G$
essentially ‘inherits’ any lower bound on the minimum total degree of
$G$
essentially ‘inherits’ any lower bound on the minimum total degree of
![]() $G$
.
$G$
.
Proposition 4.2.
Let
![]() $0\lt \varepsilon \leq d/2$
and let
$0\lt \varepsilon \leq d/2$
and let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex digraph such that
$n$
-vertex digraph such that
![]() $\delta (G)\geq \alpha n$
for some
$\delta (G)\geq \alpha n$
for some
![]() $\alpha \gt 0$
. Suppose we have applied Lemma 4.1 to
$\alpha \gt 0$
. Suppose we have applied Lemma 4.1 to
![]() $G$
to obtain the reduced digraph
$G$
to obtain the reduced digraph
![]() $R$
of
$R$
of
![]() $G$
with parameters
$G$
with parameters
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
. Then
$t_0$
. Then
![]() $\delta (R)\geq (\alpha -4d)|R|.$
$\delta (R)\geq (\alpha -4d)|R|.$
Note that when
![]() $G$
is an oriented graph, its reduced digraph
$G$
is an oriented graph, its reduced digraph
![]() $R$
is not necessarily oriented (i.e. it may contain double edges). However, if for every double edge in
$R$
is not necessarily oriented (i.e. it may contain double edges). However, if for every double edge in
![]() $R$
we retain precisely one direction (with suitable probability), we obtain an oriented subgraph
$R$
we retain precisely one direction (with suitable probability), we obtain an oriented subgraph
![]() $R_{o}$
of
$R_{o}$
of
![]() $R$
that, with positive probability, still inherits some of the properties of
$R$
that, with positive probability, still inherits some of the properties of
![]() $G$
. This argument was formalised by Kelly, Kühn, and Osthus [Reference Kelly, Kühn and Osthus23, Lemma 3.2], and in particular they proved the following result.
$G$
. This argument was formalised by Kelly, Kühn, and Osthus [Reference Kelly, Kühn and Osthus23, Lemma 3.2], and in particular they proved the following result.
Lemma 4.3 ([Reference Kelly, Kühn and Osthus23, Lemma 3.2]). For every
![]() $\varepsilon \in (0,1)$
, if
$\varepsilon \in (0,1)$
, if
![]() $t_0, n \in \mathbb N$
such that
$t_0, n \in \mathbb N$
such that
![]() $1/n \ll 1/t_0 \ll \varepsilon$
, then the following holds. Let
$1/n \ll 1/t_0 \ll \varepsilon$
, then the following holds. Let
![]() $d, \alpha \in [0,1]$
and let
$d, \alpha \in [0,1]$
and let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex oriented graph such that
$n$
-vertex oriented graph such that
![]() $\delta ^0(G) \geq \alpha n$
. Apply Lemma 4.1 to
$\delta ^0(G) \geq \alpha n$
. Apply Lemma 4.1 to
![]() $G$
to obtain the reduced digraph
$G$
to obtain the reduced digraph
![]() $R$
of
$R$
of
![]() $G$
with parameters
$G$
with parameters
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
. Then there is a spanning oriented subgraph
$t_0$
. Then there is a spanning oriented subgraph
![]() $R_o$
of
$R_o$
of
![]() $R$
such that
$R$
such that
![]() $\delta ^0(R_o)\geq (\alpha -(3\varepsilon +d))|R_o|.$
$\delta ^0(R_o)\geq (\alpha -(3\varepsilon +d))|R_o|.$
Let
![]() $G$
be a graph and
$G$
be a graph and
![]() $A,B\subseteq V(G)$
be disjoint. We define the density
$A,B\subseteq V(G)$
be disjoint. We define the density
![]() $d_G(A,B)$
analogously to before. As before, given
$d_G(A,B)$
analogously to before. As before, given
![]() $\varepsilon \gt 0$
, we say that
$\varepsilon \gt 0$
, we say that
![]() $(A,B)$
is
$(A,B)$
is
![]() $\varepsilon$
-regular in
$\varepsilon$
-regular in
![]() $G$
if for all subsets
$G$
if for all subsets
![]() $A'\subseteq A$
and
$A'\subseteq A$
and
![]() $B' \subseteq B$
with
$B' \subseteq B$
with
![]() $|A'|\gt \varepsilon |A|$
and
$|A'|\gt \varepsilon |A|$
and
![]() $|B'|\gt \varepsilon |B|$
we have
$|B'|\gt \varepsilon |B|$
we have
Given
![]() $\varepsilon , d\gt 0$
, we say that
$\varepsilon , d\gt 0$
, we say that
![]() $(A,B)$
is
$(A,B)$
is
![]() $(\varepsilon ,d)$
-superregular in
$(\varepsilon ,d)$
-superregular in
![]() $G$
if
$G$
if
![]() $(A,B)$
is
$(A,B)$
is
![]() $\varepsilon$
-regular in
$\varepsilon$
-regular in
![]() $G$
and, additionally,
$G$
and, additionally,
![]() $d_G(a) \gt d |B|$
for all
$d_G(a) \gt d |B|$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $d_G(b) \gt d |A|$
for all
$d_G(b) \gt d |A|$
for all
![]() $b \in B$
.
$b \in B$
.
The next two propositions are well-known and easy to prove properties of regular pairs.
Proposition 4.4.
Suppose that
![]() $0\lt \varepsilon \lt \xi \leq 1/2$
. Let
$0\lt \varepsilon \lt \xi \leq 1/2$
. Let
![]() $G$
be a graph and let
$G$
be a graph and let
![]() $(A,B)$
be
$(A,B)$
be
![]() $\varepsilon$
-regular in
$\varepsilon$
-regular in
![]() $G$
with density
$G$
with density
![]() $d$
. If
$d$
. If
![]() $A'\subseteq A$
and
$A'\subseteq A$
and
![]() $B'\subseteq B$
with
$B'\subseteq B$
with
![]() $|A'|\geq \xi |A|$
and
$|A'|\geq \xi |A|$
and
![]() $|B'|\geq \xi |B|$
, then
$|B'|\geq \xi |B|$
, then
![]() $(A',B')$
is
$(A',B')$
is
![]() $\varepsilon /\xi$
-regular in
$\varepsilon /\xi$
-regular in
![]() $G$
with density at least
$G$
with density at least
![]() $d-\varepsilon$
.
$d-\varepsilon$
.
Proposition 4.5.
Given
![]() $0\lt \varepsilon \lt d\leq 1$
, let
$0\lt \varepsilon \lt d\leq 1$
, let
![]() $G$
be a graph and let
$G$
be a graph and let
![]() $(A,B)$
be
$(A,B)$
be
![]() $\varepsilon$
-regular in
$\varepsilon$
-regular in
![]() $G$
with density
$G$
with density
![]() $d$
. There are at most
$d$
. There are at most
![]() $\varepsilon |A|$
vertices
$\varepsilon |A|$
vertices
![]() $v\in A$
such that
$v\in A$
such that
![]() $d_G(v, B)\leq (d-\varepsilon )|B|$
, and at most
$d_G(v, B)\leq (d-\varepsilon )|B|$
, and at most
![]() $\varepsilon |B|$
vertices
$\varepsilon |B|$
vertices
![]() $w\in B$
such that
$w\in B$
such that
![]() $d_G(w, A)\leq (d-\varepsilon )|A|$
.
$d_G(w, A)\leq (d-\varepsilon )|A|$
.
We will use the following specific version of the blow-up lemma of Komlós, Sárközy, and Szemerédi [Reference Komlós, Sárközy and Szemerédi25].
Lemma 4.6 (Blow-up lemma [Reference Komlós, Sárközy and Szemerédi25]). Let
![]() $1/m \ll \varepsilon \ll 1/\ell ,d,1/\Delta$
. Let
$1/m \ll \varepsilon \ll 1/\ell ,d,1/\Delta$
. Let
![]() $V_1, \ldots , V_{\ell }$
be pairwise disjoint sets of vertices, each of size
$V_1, \ldots , V_{\ell }$
be pairwise disjoint sets of vertices, each of size
![]() $m$
. Let
$m$
. Let
![]() $R$
be a graph with
$R$
be a graph with
![]() $V(R) = \{V_1, \ldots , V_\ell \}$
. Let
$V(R) = \{V_1, \ldots , V_\ell \}$
. Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $V_1 \cup \ldots \cup V_\ell$
such that
$V_1 \cup \ldots \cup V_\ell$
such that
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $(\varepsilon , d)$
-superregular in
$(\varepsilon , d)$
-superregular in
![]() $G$
for each
$G$
for each
![]() $V_iV_j \in E(R)$
. Let
$V_iV_j \in E(R)$
. Let
![]() $W_1,\ldots , W_\ell$
denote the vertex classes of the
$W_1,\ldots , W_\ell$
denote the vertex classes of the
![]() $m$
-blow-up
$m$
-blow-up
![]() $R(m)$
of
$R(m)$
of
![]() $R$
that correspond to
$R$
that correspond to
![]() $V_1,\ldots , V_\ell$
, respectively. If
$V_1,\ldots , V_\ell$
, respectively. If
![]() $H$
is a subgraph of
$H$
is a subgraph of
![]() $R(m)$
so that
$R(m)$
so that
![]() $\Delta (H) \le \Delta$
, then
$\Delta (H) \le \Delta$
, then
![]() $G$
contains a copy of
$G$
contains a copy of
![]() $H$
such that, for each
$H$
such that, for each
![]() $i\in [\ell ]$
, the vertices in
$i\in [\ell ]$
, the vertices in
![]() $V(H) \cap W_i$
are embedded into
$V(H) \cap W_i$
are embedded into
![]() $V_i$
in
$V_i$
in
![]() $G$
.
$G$
.
Remark 4.7. Note that, although Lemma 4.6 is stated for graphs, it is also applicable when
![]() $R$
,
$R$
,
![]() $G$
, and
$G$
, and
![]() $H$
are oriented graphs such that all edges in
$H$
are oriented graphs such that all edges in
![]() $G[V_i\cup V_j]$
are oriented from
$G[V_i\cup V_j]$
are oriented from
![]() $V_i$
to
$V_i$
to
![]() $V_j$
when
$V_j$
when
![]() $V_iV_j \in E(R)$
. Indeed, in this case, one can ‘ignore’ the orientations of the edges and then apply Lemma 4.6 to the underlying graphs of
$V_iV_j \in E(R)$
. Indeed, in this case, one can ‘ignore’ the orientations of the edges and then apply Lemma 4.6 to the underlying graphs of
![]() $R$
,
$R$
,
![]() $G$
, and
$G$
, and
![]() $H$
.
$H$
.
For example, suppose that
![]() $R$
is the
$R$
is the
![]() $k$
th power of the directed cycle
$k$
th power of the directed cycle
![]() $V_1\ldots V_{\ell }V_1$
where
$V_1\ldots V_{\ell }V_1$
where
![]() $\ell \geq 2k+1$
. Then
$\ell \geq 2k+1$
. Then
![]() $R$
is an oriented graph. Thus, in the oriented graph
$R$
is an oriented graph. Thus, in the oriented graph
![]() $R(m)$
, one can find the
$R(m)$
, one can find the
![]() $k$
th power of a Hamilton cycle by ‘winding around’ the directed cycle
$k$
th power of a Hamilton cycle by ‘winding around’ the directed cycle
![]() $V_1\ldots V_{\ell }V_1$
. Define
$V_1\ldots V_{\ell }V_1$
. Define
![]() $V_{\ell +1} \,:\!= V_1$
. Let
$V_{\ell +1} \,:\!= V_1$
. Let
![]() $G$
be the oriented graph on
$G$
be the oriented graph on
![]() $V_1 \cup \ldots \cup V_\ell$
such that, for all
$V_1 \cup \ldots \cup V_\ell$
such that, for all
![]() $i \in [\ell ]$
,
$i \in [\ell ]$
,
![]() $G[V_i,V_{i+1}]$
induces an
$G[V_i,V_{i+1}]$
induces an
![]() $(\varepsilon , d)$
-superregular pair
$(\varepsilon , d)$
-superregular pair
![]() $(V_i,V_{i+1})$
in the underlying graph of
$(V_i,V_{i+1})$
in the underlying graph of
![]() $G$
. (To emphasise, importantly all edges between
$G$
. (To emphasise, importantly all edges between
![]() $V_i$
and
$V_i$
and
![]() $V_{i+1}$
in
$V_{i+1}$
in
![]() $G$
are oriented from
$G$
are oriented from
![]() $V_i$
to
$V_i$
to
![]() $V_{i+1}$
.) Then Lemma 4.6 tells us that
$V_{i+1}$
.) Then Lemma 4.6 tells us that
![]() $G$
contains the
$G$
contains the
![]() $k$
th power of a Hamilton cycle. Note that this argument relies on
$k$
th power of a Hamilton cycle. Note that this argument relies on
![]() $R$
being an oriented graph (so does not work if
$R$
being an oriented graph (so does not work if
![]() $\ell \leq 2k$
).
$\ell \leq 2k$
).
We finish this section with the following embedding result that allows us to find long
![]() $k$
-cycles (and therefore
$k$
-cycles (and therefore
![]() $k$
-paths) in a digraph
$k$
-paths) in a digraph
![]() $G$
if its reduced digraph contains a
$G$
if its reduced digraph contains a
![]() $k$
-cycle.
$k$
-cycle.
Lemma 4.8.
Let
![]() $k,\ell , t_0 ,n \in \mathbb N$
and
$k,\ell , t_0 ,n \in \mathbb N$
and
![]() $\eta , d, \varepsilon \gt 0$
be such that
$\eta , d, \varepsilon \gt 0$
be such that
![]() $k +1 \leq \ell$
and
$k +1 \leq \ell$
and
![]() $1/n \ll 1/t_0 \ll \varepsilon \ll d, \eta , 1/\ell ,1/k$
. Let
$1/n \ll 1/t_0 \ll \varepsilon \ll d, \eta , 1/\ell ,1/k$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex digraph and suppose
$n$
-vertex digraph and suppose
![]() $R$
is the reduced digraph of
$R$
is the reduced digraph of
![]() $G$
obtained by an application of Lemma 4.1 with parameters
$G$
obtained by an application of Lemma 4.1 with parameters
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
. If
$t_0$
. If
![]() $V_1 \ldots V_{\ell }V_1$
is a copy of the
$V_1 \ldots V_{\ell }V_1$
is a copy of the
![]() $k$
-cycle
$k$
-cycle
![]() $C^k_{\ell }$
in
$C^k_{\ell }$
in
![]() $R$
, then there is a
$R$
, then there is a
![]() $k$
-cycle in
$k$
-cycle in
![]() $G[V_1 \cup \ldots \cup V_{\ell }]$
covering all but at most
$G[V_1 \cup \ldots \cup V_{\ell }]$
covering all but at most
![]() $\eta \ell |V_{1}|$
vertices.
$\eta \ell |V_{1}|$
vertices.
Recall that if
![]() $ \ell \geq 2k+1$
, then
$ \ell \geq 2k+1$
, then
![]() $C^k_{\ell }$
is an oriented graph. In this case of Lemma 4.8, one can apply Lemma 4.6 á la Remark 4.7 (with
$C^k_{\ell }$
is an oriented graph. In this case of Lemma 4.8, one can apply Lemma 4.6 á la Remark 4.7 (with
![]() $C^k_{\ell }$
playing the role of
$C^k_{\ell }$
playing the role of
![]() $R$
). However, when
$R$
). However, when
![]() $k+1 \leq \ell \leq 2k$
,
$k+1 \leq \ell \leq 2k$
,
![]() $C^k_{\ell }$
is not an oriented graph. Thus, to apply Lemma 4.6, we first divide each cluster into two so that the corresponding reduced digraph contains a copy of
$C^k_{\ell }$
is not an oriented graph. Thus, to apply Lemma 4.6, we first divide each cluster into two so that the corresponding reduced digraph contains a copy of
![]() $C^k_{2\ell }$
, which is an oriented graph since
$C^k_{2\ell }$
, which is an oriented graph since
![]() $2 \ell \geq 2k+1$
.
$2 \ell \geq 2k+1$
.
Proof of Lemma
4.8. Let
![]() $m$
be the largest integer such that
$m$
be the largest integer such that
![]() $2 m \le |V_1|$
; so
$2 m \le |V_1|$
; so
![]() $ 1 /m \ll \varepsilon$
. For each
$ 1 /m \ll \varepsilon$
. For each
![]() $i \in [\ell ]$
, let
$i \in [\ell ]$
, let
![]() $W_i, W_{\ell +i}$
be disjoint subsets of
$W_i, W_{\ell +i}$
be disjoint subsets of
![]() $V_i$
each of size
$V_i$
each of size
![]() $m$
. Define the digraph
$m$
. Define the digraph
![]() $H_o \,:\!= \bigcup _{i \in [2\ell ], \, j \in [k]}G[W_i,W_{i+j}]$
, where here the subindices are understood modulo
$H_o \,:\!= \bigcup _{i \in [2\ell ], \, j \in [k]}G[W_i,W_{i+j}]$
, where here the subindices are understood modulo
![]() $2 \ell$
. In fact, notice that crucially
$2 \ell$
. In fact, notice that crucially
![]() $H_o$
is an oriented graph, and one can view
$H_o$
is an oriented graph, and one can view
![]() $H_o$
as being obtained from a copy
$H_o$
as being obtained from a copy
![]() $W_1\ldots W_{2\ell }W_1$
of
$W_1\ldots W_{2\ell }W_1$
of
![]() $C^k_{2\ell }$
by replacing each directed edge
$C^k_{2\ell }$
by replacing each directed edge
![]() $W_iW_{i+j}$
in
$W_iW_{i+j}$
in
![]() $C^k_{2\ell }$
with the oriented graph
$C^k_{2\ell }$
with the oriented graph
![]() $G[W_i,W_{i+j}]$
.
$G[W_i,W_{i+j}]$
.
Let
![]() $H$
be the underlying graph of
$H$
be the underlying graph of
![]() $H_o$
. Consider
$H_o$
. Consider
![]() $i \in [2\ell ]$
and
$i \in [2\ell ]$
and
![]() $j \in [k]$
. By Proposition 4.4,
$j \in [k]$
. By Proposition 4.4,
![]() $(W_i,W_{i+j})$
is
$(W_i,W_{i+j})$
is
![]() $3\varepsilon$
-regular in
$3\varepsilon$
-regular in
![]() $H$
with density at least
$H$
with density at least
![]() $d-\varepsilon$
. By Proposition 4.5, there are at most
$d-\varepsilon$
. By Proposition 4.5, there are at most
![]() $3\varepsilon m$
vertices
$3\varepsilon m$
vertices
![]() $v$
in each of
$v$
in each of
![]() $W_i$
and
$W_i$
and
![]() $W_{i+j}$
such that
$W_{i+j}$
such that
![]() $d_{H[W_i,W_{i+j}]} (v) \le (d -4 \varepsilon )m$
. Let
$d_{H[W_i,W_{i+j}]} (v) \le (d -4 \varepsilon )m$
. Let
![]() $d' \,:\!= d - 6 ( k+1 ) \varepsilon$
and
$d' \,:\!= d - 6 ( k+1 ) \varepsilon$
and
![]() $m' \,:\!= (1 - 6k \varepsilon )m \ge m/2$
. There exists
$m' \,:\!= (1 - 6k \varepsilon )m \ge m/2$
. There exists
![]() $W'_i \subseteq W_i$
of size
$W'_i \subseteq W_i$
of size
![]() $m'$
for each
$m'$
for each
![]() $i \in [2\ell ]$
such that, for each
$i \in [2\ell ]$
such that, for each
![]() $i \in [2 \ell ]$
and
$i \in [2 \ell ]$
and
![]() $j \in [k]$
,
$j \in [k]$
,
![]() $(W'_i,W'_{i+j})$
is
$(W'_i,W'_{i+j})$
is
![]() $( 6\varepsilon , d')$
-superregular in
$( 6\varepsilon , d')$
-superregular in
![]() $H$
. Indeed, this can be achieved by removing the
$H$
. Indeed, this can be achieved by removing the
![]() $3 \varepsilon m$
vertices in each of
$3 \varepsilon m$
vertices in each of
![]() $W_i$
and
$W_i$
and
![]() $W_{i+j}$
of the smallest degree in
$W_{i+j}$
of the smallest degree in
![]() $H[W_i,W_{i+j}]$
, for each
$H[W_i,W_{i+j}]$
, for each
![]() $i \in [2\ell ]$
and
$i \in [2\ell ]$
and
![]() $j \in [k]$
. In particular, we have
$j \in [k]$
. In particular, we have
![]() $\delta (H[W'_i,W'_{i+j}]) \ge (d -4 \varepsilon )m - 2k \cdot 3 \varepsilon m \gt d' m'$
. Further, by Proposition 4.4,
$\delta (H[W'_i,W'_{i+j}]) \ge (d -4 \varepsilon )m - 2k \cdot 3 \varepsilon m \gt d' m'$
. Further, by Proposition 4.4,
![]() $(W'_i,W'_{i+j})$
is
$(W'_i,W'_{i+j})$
is
![]() $6\varepsilon$
-regular in
$6\varepsilon$
-regular in
![]() $H$
.
$H$
.
Let
![]() $H' \,:\!= H [W'_1 \cup \ldots \cup W'_{2\ell }]$
. Let
$H' \,:\!= H [W'_1 \cup \ldots \cup W'_{2\ell }]$
. Let
![]() $R'$
be the graph on
$R'$
be the graph on
![]() $\{W'_1, \ldots , W'_{2\ell }\}$
with
$\{W'_1, \ldots , W'_{2\ell }\}$
with
![]() $E(R') = \{ W'_iW'_{i+j}\; :\; i \in [2\ell ] \text{ and } j \in [k] \}$
; so
$E(R') = \{ W'_iW'_{i+j}\; :\; i \in [2\ell ] \text{ and } j \in [k] \}$
; so
![]() $R'$
is an (undirected) copy of
$R'$
is an (undirected) copy of
![]() $C^k_{2\ell }$
. Let
$C^k_{2\ell }$
. Let
![]() $C^*$
be a copy of
$C^*$
be a copy of
![]() $C^k_{2\ell m' }$
in
$C^k_{2\ell m' }$
in
![]() $R'(m')$
obtained by ‘winding around’
$R'(m')$
obtained by ‘winding around’
![]() $R'$
. We now apply Lemma 4.6 with
$R'$
. We now apply Lemma 4.6 with
![]() $(6\varepsilon , d', 2\ell ,2k,H',R',C^*)$
playing the role of
$(6\varepsilon , d', 2\ell ,2k,H',R',C^*)$
playing the role of
![]() $ (\varepsilon , d, \ell ,\Delta ,G,R,H)$
to obtain a copy of
$ (\varepsilon , d, \ell ,\Delta ,G,R,H)$
to obtain a copy of
![]() $C^k_{2\ell m' }$
in
$C^k_{2\ell m' }$
in
![]() $H$
. This corresponds to an (oriented) copy of
$H$
. This corresponds to an (oriented) copy of
![]() $C^k_{ 2\ell m' }$
in
$C^k_{ 2\ell m' }$
in
![]() $G[V_1 \cup \ldots \cup V_{\ell }]$
covering all but at most
$G[V_1 \cup \ldots \cup V_{\ell }]$
covering all but at most
![]() $(1 + 12k \varepsilon m )\ell \le \eta \ell |V_1|$
vertices.
$(1 + 12k \varepsilon m )\ell \le \eta \ell |V_1|$
vertices.
5. Directed graphs: almost covering, absorbing, and connecting lemmas for Theorem1.4
As mentioned in Section 2, the proof of Theorem1.4 relies on three main auxiliary results: an almost covering lemma, an absorbing lemma, and a connecting lemma. In this section, we prove these three results; see Lemmas 5.2, 5.5, and 5.14.
Recall that Theorem1.4 corresponds to the
![]() $k=2$
case of Conjecture 1.3. Our almost covering lemma and absorbing lemma actually hold for all
$k=2$
case of Conjecture 1.3. Our almost covering lemma and absorbing lemma actually hold for all
![]() $k\geq 2$
. In fact, the almost covering lemma requires a weaker minimum total degree condition than that in Conjecture 1.3. However, our connecting lemma only deals with the
$k\geq 2$
. In fact, the almost covering lemma requires a weaker minimum total degree condition than that in Conjecture 1.3. However, our connecting lemma only deals with the
![]() $k=2$
case. Consequently, the only ingredient missing for a full proof of the asymptotic version of Conjecture 1.3 is a connecting lemma for
$k=2$
case. Consequently, the only ingredient missing for a full proof of the asymptotic version of Conjecture 1.3 is a connecting lemma for
![]() $k\geq 3$
. We suspect though that obtaining such a connecting lemma will be rather challenging; we discuss this further in Section 8.
$k\geq 3$
. We suspect though that obtaining such a connecting lemma will be rather challenging; we discuss this further in Section 8.
5.1 Almost covering lemma
Given
![]() $k\geq 3$
, let
$k\geq 3$
, let
![]() $\overline {K}_{k}$
denote the digraph obtained from the complete digraph on
$\overline {K}_{k}$
denote the digraph obtained from the complete digraph on
![]() $k$
vertices by deleting a matching on
$k$
vertices by deleting a matching on
![]() $\big \lfloor \tfrac {k}{2}\big \rfloor$
edges. In particular, note that
$\big \lfloor \tfrac {k}{2}\big \rfloor$
edges. In particular, note that
![]() $C_{k+2}^{k}\subseteq \overline {K}_{k+2}$
, but
$C_{k+2}^{k}\subseteq \overline {K}_{k+2}$
, but
![]() $C_{k+1}^{k}\not \subseteq \overline {K}_{k+1}$
.Footnote
4
$C_{k+1}^{k}\not \subseteq \overline {K}_{k+1}$
.Footnote
4
The following result was proven in [Reference Czygrinow, DeBiasio, Molla and Treglown8, Theorem 6.1].
Theorem 5.1 (Czygrinow, DeBiasio, Molla and Treglown [Reference Czygrinow, DeBiasio, Molla and Treglown8]). Given any
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $\eta \gt 0$
, there exists an
$\eta \gt 0$
, there exists an
![]() $n_0\in \mathbb N$
such that for every
$n_0\in \mathbb N$
such that for every
![]() $n\geq n_0$
, the following holds. If
$n\geq n_0$
, the following holds. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex digraph with
$n$
-vertex digraph with
then
![]() $G$
contains a
$G$
contains a
![]() $\overline {K}_{k}$
-tiling covering all but at most
$\overline {K}_{k}$
-tiling covering all but at most
![]() $\eta n$
vertices.
$\eta n$
vertices.
We use Theorem5.1 to prove the almost covering lemma.
Lemma 5.2 (Almost covering lemma for total degree in digraphs). Given any integer
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $\eta \gt 0$
, there exist
$\eta \gt 0$
, there exist
![]() $n_0,\,T\in \mathbb N$
such that for any
$n_0,\,T\in \mathbb N$
such that for any
![]() $n\geq n_0$
, the following holds. If
$n\geq n_0$
, the following holds. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex digraph with
$n$
-vertex digraph with
then
![]() $G$
contains a collection of at most
$G$
contains a collection of at most
![]() $T$
vertex-disjoint
$T$
vertex-disjoint
![]() $k$
-paths that covers all but at most
$k$
-paths that covers all but at most
![]() $\eta n$
vertices.
$\eta n$
vertices.
Proof. Define constants
![]() $\varepsilon , \xi , d\gt 0$
and
$\varepsilon , \xi , d\gt 0$
and
![]() $n_0,t_0,T \in \mathbb N$
such that
$n_0,t_0,T \in \mathbb N$
such that
and where
![]() $T$
is the output of Lemma 4.1 on input
$T$
is the output of Lemma 4.1 on input
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $t_0$
.
$t_0$
.
Let
![]() $G$
be a digraph on
$G$
be a digraph on
![]() $n \geq n_0$
vertices as in the statement of the lemma. Apply Lemma 4.1 with parameters
$n \geq n_0$
vertices as in the statement of the lemma. Apply Lemma 4.1 with parameters
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $d$
, and
$d$
, and
![]() $t_0$
to obtain the reduced digraph
$t_0$
to obtain the reduced digraph
![]() $R$
of
$R$
of
![]() $G$
with
$G$
with
![]() $t_0\lt |R|\lt T$
. Let
$t_0\lt |R|\lt T$
. Let
![]() $m$
denote the size of the clusters of
$m$
denote the size of the clusters of
![]() $G$
. By Proposition 4.2 and (5.1),
$G$
. By Proposition 4.2 and (5.1),
Thus, Theorem5.1 yields a
![]() $\overline {K}_{k+2}$
-tiling
$\overline {K}_{k+2}$
-tiling
![]() $\mathcal T$
in
$\mathcal T$
in
![]() $R$
covering all but at most
$R$
covering all but at most
![]() $\eta |R| /2$
of the
$\eta |R| /2$
of the
![]() $V_i \in V(R)$
.
$V_i \in V(R)$
.
Recall that
![]() $C_{k+2}^{k}\subseteq \overline {K}_{k+2}$
. Therefore, for each tile
$C_{k+2}^{k}\subseteq \overline {K}_{k+2}$
. Therefore, for each tile
![]() $\overline {K}_{k+2}$
in
$\overline {K}_{k+2}$
in
![]() $\mathcal T$
formed by clusters
$\mathcal T$
formed by clusters
![]() $V_{i_1},\ldots , V_{i_{k+2}}$
, we may apply Lemma 4.8 with
$V_{i_1},\ldots , V_{i_{k+2}}$
, we may apply Lemma 4.8 with
![]() $\xi$
playing the role of
$\xi$
playing the role of
![]() $\eta$
, to obtain a
$\eta$
, to obtain a
![]() $k$
-path in
$k$
-path in
![]() $G[\bigcup _{j\in [k+2]} V_{i_j}]$
covering all but at most
$G[\bigcup _{j\in [k+2]} V_{i_j}]$
covering all but at most
![]() $\xi (k+2)m$
vertices from
$\xi (k+2)m$
vertices from
![]() $\bigcup _{j\in [k+2]} V_{i_j}$
.
$\bigcup _{j\in [k+2]} V_{i_j}$
.
Together, these
![]() $k$
-paths form a collection of size at most
$k$
-paths form a collection of size at most
![]() $|R|\lt T$
. Moreover, all but at most
$|R|\lt T$
. Moreover, all but at most
vertices of
![]() $G$
are covered by these
$G$
are covered by these
![]() $k$
-paths, as desired.
$k$
-paths, as desired.
5.2 Absorbing lemma
In [Reference Czygrinow, DeBiasio, Molla and Treglown8, Theorem 4.2], the maximum number of edges in an
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
without a copy of
$G$
without a copy of
![]() $\overline {K}_{k}$
was determined for all
$\overline {K}_{k}$
was determined for all
![]() $k, n\in \mathbb{N}$
. Using this result together with a standard supersaturation argument (e.g. via Lemma 4.1), one can easily obtain the following theorem for the
$k, n\in \mathbb{N}$
. Using this result together with a standard supersaturation argument (e.g. via Lemma 4.1), one can easily obtain the following theorem for the
![]() $t$
-blow-up
$t$
-blow-up
![]() $\overline {K}_{k}(t)$
.
$\overline {K}_{k}(t)$
.
Theorem 5.3.
Let
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $\eta \gt 0$
, and
$\eta \gt 0$
, and
![]() $t\in \mathbb{N}$
. There exist
$t\in \mathbb{N}$
. There exist
![]() $n_0\in \mathbb N$
and
$n_0\in \mathbb N$
and
![]() $\xi \gt 0$
such that every digraph
$\xi \gt 0$
such that every digraph
![]() $G$
on
$G$
on
![]() $n\geq n_0$
vertices with
$n\geq n_0$
vertices with
![]() $e(G)\geq \big (1-\frac {1}{k-1}+\eta \big )n^2$
contains at least
$e(G)\geq \big (1-\frac {1}{k-1}+\eta \big )n^2$
contains at least
![]() $\xi n^{kt}$
copies of
$\xi n^{kt}$
copies of
![]() $\overline {K}_{k}(t)$
.
$\overline {K}_{k}(t)$
.
The following definition is a crucial notion needed for constructing an absorbing
![]() $k$
-path.
$k$
-path.
Definition 5.4.
For a digraph
![]() $G$
and
$G$
and
![]() $v\in V(G)$
, we say a
$v\in V(G)$
, we say a
![]() $k$
-path on
$k$
-path on
![]() $2(k+2)$
vertices
$2(k+2)$
vertices
![]() $P_v = v_1 \ldots v_{2(k+2)}$
in
$P_v = v_1 \ldots v_{2(k+2)}$
in
![]() $G$
is an absorber for
$G$
is an absorber for
![]() $v$
if
$v$
if
![]() $v_1\ldots v_{k+2}\, v\, v_{k+3} \ldots v_{2(k+2)}$
is also a
$v_1\ldots v_{k+2}\, v\, v_{k+3} \ldots v_{2(k+2)}$
is also a
![]() $k$
-path in
$k$
-path in
![]() $G$
.
$G$
.
We are now ready to state our absorbing lemma for digraphs.
Lemma 5.5 (Absorbing lemma for total degree in digraphs). Given
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $\eta \gt 0$
, there exist
$\eta \gt 0$
, there exist
![]() $n_0\in \mathbb N$
and
$n_0\in \mathbb N$
and
![]() $\xi \gt 0$
so that for any
$\xi \gt 0$
so that for any
![]() $n\geq n_0$
, the following holds. If
$n\geq n_0$
, the following holds. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex digraph with
$n$
-vertex digraph with
then, for every vertex
![]() $v\in V(G)$
, there are at least
$v\in V(G)$
, there are at least
![]() $\xi n^{2(k+2)}$
absorbers
$\xi n^{2(k+2)}$
absorbers
![]() $P_v$
for
$P_v$
for
![]() $v$
in
$v$
in
![]() $G$
.
$G$
.
Proof. Let
![]() $\xi _1 \gt 0$
be the output of Theorem5.3 on input
$\xi _1 \gt 0$
be the output of Theorem5.3 on input
![]() $k+2$
,
$k+2$
,
![]() $\eta$
, and
$\eta$
, and
![]() $t=2$
. Let
$t=2$
. Let
![]() $n_0 \in \mathbb N$
be sufficiently large and let
$n_0 \in \mathbb N$
be sufficiently large and let
![]() $G$
be a digraph on
$G$
be a digraph on
![]() $n \geq n_0$
vertices as in the statement of the lemma.
$n \geq n_0$
vertices as in the statement of the lemma.
Given any
![]() $v\in V(G)$
note that
$v\in V(G)$
note that
Let
![]() $U$
be a subset of
$U$
be a subset of
![]() $N^{+}_G(v)\cap N^-_G(v)$
of size
$N^{+}_G(v)\cap N^-_G(v)$
of size
![]() $\tfrac {k+1}{k+3}n$
. Observe that
$\tfrac {k+1}{k+3}n$
. Observe that
and in particular
![]() $e(G[U])\geq \big (\tfrac {k}{k+1}+\eta )|U|^2$
. Thus, Theorem5.3 yields at least
$e(G[U])\geq \big (\tfrac {k}{k+1}+\eta )|U|^2$
. Thus, Theorem5.3 yields at least
![]() $\xi _1 |U|^{2(k+2)} \geq \xi _1 (n/2)^{2(k+2)}$
copies of
$\xi _1 |U|^{2(k+2)} \geq \xi _1 (n/2)^{2(k+2)}$
copies of
![]() $\overline {K}_{k+2}(2)$
in
$\overline {K}_{k+2}(2)$
in
![]() $G[U]$
. Set
$G[U]$
. Set
![]() $\xi \,:\!= \xi _1 /2^{2(k+2)}$
.
$\xi \,:\!= \xi _1 /2^{2(k+2)}$
.
As
![]() $C^{k}_{k+2} \subseteq \overline {K}_{k+2}$
, it is easy to see that each such copy of
$C^{k}_{k+2} \subseteq \overline {K}_{k+2}$
, it is easy to see that each such copy of
![]() $\overline {K}_{k+2}(2)$
in
$\overline {K}_{k+2}(2)$
in
![]() $G[U]$
is spanned by a
$G[U]$
is spanned by a
![]() $k$
-path. Moreover, as
$k$
-path. Moreover, as
![]() $U \subseteq N^{+}_G(v)\cap N^-_G(v)$
, each of these
$U \subseteq N^{+}_G(v)\cap N^-_G(v)$
, each of these
![]() $k$
-paths is an absorber for
$k$
-paths is an absorber for
![]() $v$
, as desired.
$v$
, as desired.
5.3 Connecting lemma
The full version of our connecting lemma (Lemma 5.14) is stated at the end of this section. Before this, we introduce a few preliminary definitions and results.
Given a digraph
![]() $G$
, let
$G$
, let
![]() $G^{\pm }$
be the graph with vertex set
$G^{\pm }$
be the graph with vertex set
![]() $V(G)$
such that
$V(G)$
such that
![]() $ab \in E(G^{\pm })$
if and only if
$ab \in E(G^{\pm })$
if and only if
![]() $ab,ba \in E(G)$
. For a vertex
$ab,ba \in E(G)$
. For a vertex
![]() $v \in V(G)$
and
$v \in V(G)$
and
![]() $X \subseteq V(G)$
, recall that
$X \subseteq V(G)$
, recall that
![]() $d_G(v,X) = d^+_G(v,X) + d^-_G(v,X)$
. Given
$d_G(v,X) = d^+_G(v,X) + d^-_G(v,X)$
. Given
![]() $U, W \subseteq V(G)$
and
$U, W \subseteq V(G)$
and
![]() $m \in {\mathbb{N}}$
, define
$m \in {\mathbb{N}}$
, define
![]() $N_{=m}(U, W) \,:\!= \{ w \in W\; :\; d_G(w,U) =m \}$
and
$N_{=m}(U, W) \,:\!= \{ w \in W\; :\; d_G(w,U) =m \}$
and
![]() $d_{=m}(U,W) \,:\!= |N_{=m}(U, W)|$
.
$d_{=m}(U,W) \,:\!= |N_{=m}(U, W)|$
.
The following result is the starting point for our connecting lemma.
Lemma 5.6.
For
![]() $1/n \ll \gamma \lt 1$
, the following holds for every
$1/n \ll \gamma \lt 1$
, the following holds for every
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with
$G$
with
![]() $\delta (G) \ge (8/5 + \gamma )n$
. If
$\delta (G) \ge (8/5 + \gamma )n$
. If
![]() $\{A, B\}$
is a partition of
$\{A, B\}$
is a partition of
![]() $V(G)$
such that neither
$V(G)$
such that neither
![]() $A$
nor
$A$
nor
![]() $B$
is an independent set, then there exist
$B$
is an independent set, then there exist
![]() $a_1a_2 \in E(G[A])$
,
$a_1a_2 \in E(G[A])$
,
![]() $b_1b_2 \in E(G[B])$
and
$b_1b_2 \in E(G[B])$
and
![]() $xy \in E(G)$
such that
$xy \in E(G)$
such that
![]() $a_1a_2b_1b_2$
or
$a_1a_2b_1b_2$
or
![]() $a_1a_2xyb_1b_2$
is a
$a_1a_2xyb_1b_2$
is a
![]() $2$
-path.
$2$
-path.
Proof. For a contradiction, assume that
![]() $G$
is an
$G$
is an
![]() $n$
-vertex digraph and
$n$
-vertex digraph and
![]() $ \{ A, B \}$
is a partition of
$ \{ A, B \}$
is a partition of
![]() $V(G)$
that together form a counterexample to the lemma. By considering the digraph with all orientations reversed, we may assume without loss of generality that
$V(G)$
that together form a counterexample to the lemma. By considering the digraph with all orientations reversed, we may assume without loss of generality that
![]() $|A| \ge |B|$
. Define
$|A| \ge |B|$
. Define
By our assumption,
![]() $E_A \cap E_B = \emptyset$
. Note that, for every
$E_A \cap E_B = \emptyset$
. Note that, for every
![]() $ab \in E(A, B)$
, we have
$ab \in E(A, B)$
, we have
![]() $d_{=4}(ab,V(G)) \ge 2\delta (G) - 3n \ge n/5 + 2\gamma n$
and so
$d_{=4}(ab,V(G)) \ge 2\delta (G) - 3n \ge n/5 + 2\gamma n$
and so
![]() $ab \in E_A \cup E_B$
. Therefore,
$ab \in E_A \cup E_B$
. Therefore,
![]() $\{E_A, E_B\}$
is a partition of
$\{E_A, E_B\}$
is a partition of
![]() $E(A, B)$
.
$E(A, B)$
.
Claim 5.7.
![]() $E_B$
is non-empty.
$E_B$
is non-empty.
Proof. Suppose not. Let
![]() $C$
be a maximal tournament in
$C$
be a maximal tournament in
![]() $G[B]$
. Since
$G[B]$
. Since
![]() $B$
is not an independent set, we have
$B$
is not an independent set, we have
![]() $|C| \ge 2$
. Note that
$|C| \ge 2$
. Note that
![]() $E_B = \emptyset$
implies that
$E_B = \emptyset$
implies that
![]() $d_G(a, C) \le |C| + 1$
for every
$d_G(a, C) \le |C| + 1$
for every
![]() $a \in A$
. Furthermore, because
$a \in A$
. Furthermore, because
![]() $C$
is a maximal tournament in
$C$
is a maximal tournament in
![]() $G[B]$
, we have
$G[B]$
, we have
![]() $d_G(b, C) \le 2|C| - 2$
for every
$d_G(b, C) \le 2|C| - 2$
for every
![]() $b \in B$
. Recall that
$b \in B$
. Recall that
![]() $|A| \ge |B|$
, so
$|A| \ge |B|$
, so
![]() $|B| - 3n/5 \lt 0$
. Hence,
$|B| - 3n/5 \lt 0$
. Hence,
 \begin{align*} |C|\delta (G) &\le \sum _{v \in C} d _G(v) \le |B|(2|C| - 2) + |A|(|C| + 1) = |C|(n + |B|) - 2|B| + |A| \\ &= 8n|C|/5 + |C|(|B| - 3n/5) - 2|B| + |A| \\ &\le 8n|C|/5 + 2(|B| - 3n/5) - 2|B| + |A| \lt 8n|C|/5, \end{align*}
\begin{align*} |C|\delta (G) &\le \sum _{v \in C} d _G(v) \le |B|(2|C| - 2) + |A|(|C| + 1) = |C|(n + |B|) - 2|B| + |A| \\ &= 8n|C|/5 + |C|(|B| - 3n/5) - 2|B| + |A| \\ &\le 8n|C|/5 + 2(|B| - 3n/5) - 2|B| + |A| \lt 8n|C|/5, \end{align*}
a contradiction to the minimum total degree condition.
By Claim 5.7, there exists
![]() $ab \in E_B$
. Set
$ab \in E_B$
. Set
Since
![]() $ab \in E_B$
, we have
$ab \in E_B$
, we have
![]() $N_{=4}(ab, A) = \emptyset$
and so
$N_{=4}(ab, A) = \emptyset$
and so
This implies that
![]() $c \gt 0$
and
$c \gt 0$
and
![]() $|B_3| + |A_3| \ge 4n/5 - 2c$
. Since
$|B_3| + |A_3| \ge 4n/5 - 2c$
. Since
![]() $|B_4| + |B_3| \le |B| \le n/2$
and
$|B_4| + |B_3| \le |B| \le n/2$
and
![]() $|B_4| = n/5 + c$
, we have
$|B_4| = n/5 + c$
, we have
![]() $|B_3| \le 3n/10 - c$
and
$|B_3| \le 3n/10 - c$
and
![]() $c \le 3n/10$
, so
$c \le 3n/10$
, so
![]() $|A_3| \ge n/2 - c \gt 0$
. Hence,
$|A_3| \ge n/2 - c \gt 0$
. Hence,
Claim 5.8.
![]() $E(A_3, B_4) = \emptyset$
.
$E(A_3, B_4) = \emptyset$
.
Proof. For a contradiction, assume that
![]() $xy \in E(A_3, B_4)$
. If
$xy \in E(A_3, B_4)$
. If
![]() $xa \in E(G)$
, then
$xa \in E(G)$
, then
![]() $xayb$
is a
$xayb$
is a
![]() $2$
-path because
$2$
-path because
![]() $y \in N_{=4}(ab, B)$
. If
$y \in N_{=4}(ab, B)$
. If
![]() $xa \notin E(G)$
, then the fact that
$xa \notin E(G)$
, then the fact that
![]() $x \in N_{=3}(ab,A)$
implies that
$x \in N_{=3}(ab,A)$
implies that
![]() $ax,xb \in E(G)$
, so
$ax,xb \in E(G)$
, so
![]() $axby$
is a
$axby$
is a
![]() $2$
-path. In both cases, we obtain a contradiction to our initial assumption that
$2$
-path. In both cases, we obtain a contradiction to our initial assumption that
![]() $G$
is a counterexample to the lemma.
$G$
is a counterexample to the lemma.
Note that
![]() $\delta (G^{\pm }) \ge \delta (G) - n \ge 3n/5 + \gamma n$
. Therefore, by (5.2) and Claim 5.8, there exist
$\delta (G^{\pm }) \ge \delta (G) - n \ge 3n/5 + \gamma n$
. Therefore, by (5.2) and Claim 5.8, there exist
![]() $a_1a_2 \in E(G^{\pm }[A_3])$
and
$a_1a_2 \in E(G^{\pm }[A_3])$
and
![]() $b_1b_2 \in E(G^{\pm }[B_4])$
. For
$b_1b_2 \in E(G^{\pm }[B_4])$
. For
![]() $i \in \{7,8\}$
set
$i \in \{7,8\}$
set
![]() $V_i \,:\!= N_{=i}(\{a_1,a_2, b_1, b_2\}, V(G))$
. Note that
$V_i \,:\!= N_{=i}(\{a_1,a_2, b_1, b_2\}, V(G))$
. Note that
![]() $32n/5 + 4 \gamma n \le 2|V_8| + |V_7| + 6n$
, so
$32n/5 + 4 \gamma n \le 2|V_8| + |V_7| + 6n$
, so
By Claim 5.8,
![]() $V_7 \cup V_8$
is disjoint from
$V_7 \cup V_8$
is disjoint from
![]() $A_3 \cup B_4$
, so
$A_3 \cup B_4$
, so
Therefore,
Let
![]() $x \in V_8$
. Since we have assumed that
$x \in V_8$
. Since we have assumed that
![]() $G$
is a counterexample to the lemma, in
$G$
is a counterexample to the lemma, in
![]() $G$
,
$G$
,
![]() $x$
has no neighbours in
$x$
has no neighbours in
![]() $V_8$
, and in
$V_8$
, and in
![]() $G^{\pm }$
,
$G^{\pm }$
,
![]() $x$
has no neighbours in
$x$
has no neighbours in
![]() $V_7$
. Thus,
$V_7$
. Thus,
a contradiction.
Definition 5.9.
In a digraph
![]() $G$
, a
$G$
, a
![]() $2$
-walk of length
$2$
-walk of length
![]() $\ell$
is a sequence
$\ell$
is a sequence
![]() $v_1 \dotsc v_\ell$
of vertices from
$v_1 \dotsc v_\ell$
of vertices from
![]() $V(G)$
such that, for every
$V(G)$
such that, for every
![]() $i \in [\ell - 1]$
, we have
$i \in [\ell - 1]$
, we have
![]() $v_iv_{i+1} \in E(G)$
, and moreover, for every
$v_iv_{i+1} \in E(G)$
, and moreover, for every
![]() $j \in [\ell - 2]$
, we have
$j \in [\ell - 2]$
, we have
![]() $ v_jv_{j+2} \in E(G)$
. Note that the vertices
$ v_jv_{j+2} \in E(G)$
. Note that the vertices
![]() $v_1, \dotsc , v_\ell \in V(G)$
are not necessarily distinct.
$v_1, \dotsc , v_\ell \in V(G)$
are not necessarily distinct.
The notion of a
![]() $2$
-walk is used in the proof of the following result.
$2$
-walk is used in the proof of the following result.
Lemma 5.10.
Let
![]() $0 \lt 1/n \ll \gamma \lt 1$
. If
$0 \lt 1/n \ll \gamma \lt 1$
. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex digraph with
$n$
-vertex digraph with
![]() $\delta (G)\geq (8/5+\gamma )n$
, then for every pair of disjoint edges
$\delta (G)\geq (8/5+\gamma )n$
, then for every pair of disjoint edges
![]() $ab, yz \in E(G)$
, there exists a
$ab, yz \in E(G)$
, there exists a
![]() $2$
-path
$2$
-path
![]() $x_1x_2 \ldots x_{\ell -1}x_{\ell }$
of length
$x_1x_2 \ldots x_{\ell -1}x_{\ell }$
of length
![]() $\ell \leq 20$
where
$\ell \leq 20$
where
![]() $x_1=a$
,
$x_1=a$
,
![]() $x_2=b$
,
$x_2=b$
,
![]() $x_{\ell -1}=y$
, and
$x_{\ell -1}=y$
, and
![]() $x_\ell =z$
.
$x_\ell =z$
.
Proof. Let
![]() $\sigma \gt 0$
be such that
$\sigma \gt 0$
be such that
![]() $1/n\ll \sigma \ll \gamma$
. Take
$1/n\ll \sigma \ll \gamma$
. Take
![]() $G$
,
$G$
,
![]() $ab$
, and
$ab$
, and
![]() $yz$
as in the statement of the lemma. For
$yz$
as in the statement of the lemma. For
![]() $\ell \ge 3$
, let
$\ell \ge 3$
, let
and
Claim 5.11.
For every
![]() $\ell \ge 3$
, we have
$\ell \ge 3$
, we have
![]() $|\overrightarrow {{}^{ab}{}{V}}_\ell |, |\overrightarrow {V^{yz}}_\ell | \ge n/5$
.
$|\overrightarrow {{}^{ab}{}{V}}_\ell |, |\overrightarrow {V^{yz}}_\ell | \ge n/5$
.
Proof. We will only show that
![]() $|\overrightarrow {{}^{ab}{}{V}}_\ell | \ge n/5$
since the proof that
$|\overrightarrow {{}^{ab}{}{V}}_\ell | \ge n/5$
since the proof that
![]() $|\overrightarrow {V^{yz}}_\ell | \ge n/5$
follows analogously.
$|\overrightarrow {V^{yz}}_\ell | \ge n/5$
follows analogously.
Let
![]() $\Phi _{2}\, :\!= \{ab\}$
. For
$\Phi _{2}\, :\!= \{ab\}$
. For
![]() $t \ge 3$
, let
$t \ge 3$
, let
![]() $\Phi _{t}$
be the collection of
$\Phi _{t}$
be the collection of
![]() $2$
-walks of length
$2$
-walks of length
![]() $t$
in
$t$
in
![]() $G$
that start with the edge
$G$
that start with the edge
![]() $ab$
. Since
$ab$
. Since
![]() $\delta ^+(G) \ge (3n/5 + \gamma ) n$
, for all
$\delta ^+(G) \ge (3n/5 + \gamma ) n$
, for all
![]() $t \geq 3$
we have that
$t \geq 3$
we have that
For a contradiction, suppose that
![]() $|\overrightarrow {{}^{ab}{}{V}}_\ell | \lt n/5$
. Hence the number of
$|\overrightarrow {{}^{ab}{}{V}}_\ell | \lt n/5$
. Hence the number of
![]() $2$
-walks in
$2$
-walks in
![]() $\Phi _{\ell }$
that end with a vertex in
$\Phi _{\ell }$
that end with a vertex in
![]() $\overrightarrow {{}^{ab}{}{V}}_\ell$
is less than
$\overrightarrow {{}^{ab}{}{V}}_\ell$
is less than
![]() $|\Phi _{\ell -1}|n/5$
. So the number of
$|\Phi _{\ell -1}|n/5$
. So the number of
![]() $2$
-walks in
$2$
-walks in
![]() $\Phi _\ell$
that end at a vertex not in
$\Phi _\ell$
that end at a vertex not in
![]() $\overrightarrow {{}^{ab}{}{V}}_\ell$
is at least
$\overrightarrow {{}^{ab}{}{V}}_\ell$
is at least
By an averaging argument, there exists a vertex
![]() $v \in V(G) {\setminus} \overrightarrow {{}^{ab}{}{V}}_\ell$
that is the end vertex of at least
$v \in V(G) {\setminus} \overrightarrow {{}^{ab}{}{V}}_\ell$
that is the end vertex of at least
![]() $\sigma ^{\ell -3} n^{\ell -3}$
$\sigma ^{\ell -3} n^{\ell -3}$
![]() $2$
-walks in
$2$
-walks in
![]() $\Phi _{\ell }$
, a contradiction.
$\Phi _{\ell }$
, a contradiction.
Let
![]() $\{V^+, V^-\}$
be the partition of
$\{V^+, V^-\}$
be the partition of
![]() $V(G)$
such that for every
$V(G)$
such that for every
![]() $v \in V^-$
we have
$v \in V^-$
we have
![]() $d^-_G(v) \ge d^+_G(v)$
and for every
$d^-_G(v) \ge d^+_G(v)$
and for every
![]() $v \in V^+$
we have
$v \in V^+$
we have
![]() $d^+_G(v) \gt d^-_G(v)$
.
$d^+_G(v) \gt d^-_G(v)$
.
Claim 5.12.
For
![]() $\ell \ge 5$
, we have
$\ell \ge 5$
, we have
![]() $V^- \subseteq \overrightarrow {{}^{ab}{}{V}}_\ell$
and
$V^- \subseteq \overrightarrow {{}^{ab}{}{V}}_\ell$
and
![]() $V^+ \subseteq \overrightarrow {V^{yz}}_\ell$
.
$V^+ \subseteq \overrightarrow {V^{yz}}_\ell$
.
Proof. We will only show that
![]() $V^- \subseteq \overrightarrow {{}^{ab}{}{V}}_\ell$
as the proof that
$V^- \subseteq \overrightarrow {{}^{ab}{}{V}}_\ell$
as the proof that
![]() $V^+ \subseteq \overrightarrow {V^{yz}}_\ell$
is analogous. Let
$V^+ \subseteq \overrightarrow {V^{yz}}_\ell$
is analogous. Let
![]() $v \in V^-$
. By Claim 5.11 and the fact that
$v \in V^-$
. By Claim 5.11 and the fact that
![]() $v \in V^-$
, we have
$v \in V^-$
, we have
Therefore, there are at least
![]() $(\sigma n)^{\ell - 5}\times \gamma n/2 \geq (\sigma n)^{\ell - 4}$
$(\sigma n)^{\ell - 5}\times \gamma n/2 \geq (\sigma n)^{\ell - 4}$
![]() $2$
-walks
$2$
-walks
![]() $abv_3 \dotsc v_{\ell -3} v_{\ell -2}$
in
$abv_3 \dotsc v_{\ell -3} v_{\ell -2}$
in
![]() $G$
with
$G$
with
![]() $v_{\ell -2} \in N^-_G(v)$
. Furthermore, for every such
$v_{\ell -2} \in N^-_G(v)$
. Furthermore, for every such
![]() $2$
-walk, we have
$2$
-walk, we have
and for every
![]() $v_{\ell - 1} \in N^+_G(v_{\ell -3}) \cap N^+_G(v_{\ell -2}) \cap N^-_G(v)$
, the sequence
$v_{\ell - 1} \in N^+_G(v_{\ell -3}) \cap N^+_G(v_{\ell -2}) \cap N^-_G(v)$
, the sequence
is a
![]() $2$
-walk in
$2$
-walk in
![]() $G$
. Thus, there are at least
$G$
. Thus, there are at least
![]() $(\sigma n)^{\ell - 4} \times 2 \gamma n \geq (\sigma n)^{\ell - 3}$
$(\sigma n)^{\ell - 4} \times 2 \gamma n \geq (\sigma n)^{\ell - 3}$
![]() $2$
-walks in
$2$
-walks in
![]() $G$
that start with
$G$
that start with
![]() $ab$
and end at
$ab$
and end at
![]() $v$
. Hence,
$v$
. Hence,
![]() $v \in \overrightarrow {{}^{ab}{}{V}}_\ell$
and so
$v \in \overrightarrow {{}^{ab}{}{V}}_\ell$
and so
![]() $V^- \subseteq \overrightarrow {{}^{ab}{}{V}}_\ell$
, as desired.
$V^- \subseteq \overrightarrow {{}^{ab}{}{V}}_\ell$
, as desired.
For
![]() $\ell \ge 4$
, define
$\ell \ge 4$
, define
and
Let
![]() $X^- \subseteq V^-$
be such that
$X^- \subseteq V^-$
be such that
![]() $|X^-| = \min \{\sigma n, |V^-|\}$
and
$|X^-| = \min \{\sigma n, |V^-|\}$
and
![]() $d^+_G(x) \ge d^+_G(y)$
for every
$d^+_G(x) \ge d^+_G(y)$
for every
![]() $x \in X^-$
and
$x \in X^-$
and
![]() $y \in V^- {\setminus} X^-$
. Similarly, let
$y \in V^- {\setminus} X^-$
. Similarly, let
![]() $X^+ \subseteq V^+$
be such that
$X^+ \subseteq V^+$
be such that
![]() $|X^+| = \min \{\sigma n, |V^+|\}$
and
$|X^+| = \min \{\sigma n, |V^+|\}$
and
![]() $d^-_G(x) \ge d^- _G(y)$
for every
$d^-_G(x) \ge d^- _G(y)$
for every
![]() $x \in X^+$
and
$x \in X^+$
and
![]() $y \in V^+ {\setminus} X^+$
. Set
$y \in V^+ {\setminus} X^+$
. Set
![]() $Y^- \,:\!= V^- {\setminus} X^-$
and
$Y^- \,:\!= V^- {\setminus} X^-$
and
![]() $Y^+ \,:\!= V^+ {\setminus} X^+$
.
$Y^+ \,:\!= V^+ {\setminus} X^+$
.
Claim 5.13.
For every
![]() $\ell \ge 9$
,
$\ell \ge 9$
,
![]() $E(G[Y^-]) \subseteq \overrightarrow {{}^{ab}{}{E}}_\ell$
and
$E(G[Y^-]) \subseteq \overrightarrow {{}^{ab}{}{E}}_\ell$
and
![]() $E(G[Y^+]) \subseteq \overrightarrow {E^{yz}}_\ell$
.
$E(G[Y^+]) \subseteq \overrightarrow {E^{yz}}_\ell$
.
Proof. We will only show that
![]() $E(G[Y^-]) \subseteq \overrightarrow {{}^{ab}{}{E}}_\ell$
since the proof that
$E(G[Y^-]) \subseteq \overrightarrow {{}^{ab}{}{E}}_\ell$
since the proof that
![]() $E(G[Y^+]) \subseteq \overrightarrow {E^{yz}}_\ell$
is analogous. We may assume that
$E(G[Y^+]) \subseteq \overrightarrow {E^{yz}}_\ell$
is analogous. We may assume that
![]() $E(G[Y^-]) \neq \emptyset$
and so
$E(G[Y^-]) \neq \emptyset$
and so
![]() $|X^-| = \sigma n$
. Let
$|X^-| = \sigma n$
. Let
![]() $cd \in E(G[Y^-])$
. Pick
$cd \in E(G[Y^-])$
. Pick
![]() $v_{\ell -4} \in X^-$
; by Claim 5.12,
$v_{\ell -4} \in X^-$
; by Claim 5.12,
![]() $v_{\ell -4} \in \overrightarrow {{}^{ab}{}{V}}_{\ell -4}$
. Therefore, there are at least
$v_{\ell -4} \in \overrightarrow {{}^{ab}{}{V}}_{\ell -4}$
. Therefore, there are at least
![]() $(\sigma n)^{\ell -7}$
$(\sigma n)^{\ell -7}$
![]() $2$
-walks
$2$
-walks
![]() $W$
of length
$W$
of length
![]() $\ell -4$
in
$\ell -4$
in
![]() $G$
that start with
$G$
that start with
![]() $ab$
and end with
$ab$
and end with
![]() $v_{\ell -4}$
. Let
$v_{\ell -4}$
. Let
![]() $v_{\ell -5}$
be the penultimate vertex on any such
$v_{\ell -5}$
be the penultimate vertex on any such
![]() $2$
-walk
$2$
-walk
![]() $W$
. There are more than
$W$
. There are more than
![]() $2(\delta (G) - n) + \delta (G)/2 - 2n \ge 2\gamma n$
vertices in
$2(\delta (G) - n) + \delta (G)/2 - 2n \ge 2\gamma n$
vertices in
![]() $N^+_G(v_{\ell -5}) \cap N^+_G(v_{\ell -4}) \cap N^-_G(c)$
. Let
$N^+_G(v_{\ell -5}) \cap N^+_G(v_{\ell -4}) \cap N^-_G(c)$
. Let
![]() $v_{\ell -3}$
be such a vertex.
$v_{\ell -3}$
be such a vertex.
There are at least
![]() $\gamma n$
vertices
$\gamma n$
vertices
![]() $v_{\ell -2}$
in
$v_{\ell -2}$
in
![]() $N^+_G(v_{\ell -4}) \cap N^+_G(v_{\ell -3}) \cap N^-_G(c) \cap N^-_G(d)$
. To see this, recall that
$N^+_G(v_{\ell -4}) \cap N^+_G(v_{\ell -3}) \cap N^-_G(c) \cap N^-_G(d)$
. To see this, recall that
![]() $v_{\ell - 4} \in X^-$
and
$v_{\ell - 4} \in X^-$
and
![]() $c,d \in Y^- \subseteq V^-$
, so
$c,d \in Y^- \subseteq V^-$
, so
![]() $d^+_G(v_{\ell -4}) \ge d^+_G(c)$
and
$d^+_G(v_{\ell -4}) \ge d^+_G(c)$
and
![]() $d^-_G(d) \ge \delta (G)/2$
. Therefore,
$d^-_G(d) \ge \delta (G)/2$
. Therefore,
In summary, there are
![]() $\sigma n$
choices for
$\sigma n$
choices for
![]() $v_{\ell -4}$
; at least
$v_{\ell -4}$
; at least
![]() $(\sigma n)^{\ell -7}$
choices for the
$(\sigma n)^{\ell -7}$
choices for the
![]() $2$
-walk
$2$
-walk
![]() $W$
; at least
$W$
; at least
![]() $2 \gamma n$
choices for
$2 \gamma n$
choices for
![]() $v_{\ell -3}$
; at least
$v_{\ell -3}$
; at least
![]() $\gamma n$
choices for
$\gamma n$
choices for
![]() $v_{\ell -2}$
. By the choice of
$v_{\ell -2}$
. By the choice of
![]() $v_{\ell -3}$
and
$v_{\ell -3}$
and
![]() $v_{\ell -2}$
, adding
$v_{\ell -2}$
, adding
![]() $v_{\ell -3}v_{\ell -2}cd$
to the end of
$v_{\ell -3}v_{\ell -2}cd$
to the end of
![]() $W$
yields a
$W$
yields a
![]() $2$
-walk of length
$2$
-walk of length
![]() $\ell$
in
$\ell$
in
![]() $G$
that starts with
$G$
that starts with
![]() $ab$
and ends with
$ab$
and ends with
![]() $cd$
. In total, this process gives rise to at least
$cd$
. In total, this process gives rise to at least
such
![]() $2$
-walks. Thus,
$2$
-walks. Thus,
![]() $cd \in \overrightarrow {{}^{ab}{}{E}}_\ell$
and so
$cd \in \overrightarrow {{}^{ab}{}{E}}_\ell$
and so
![]() $E(G[Y^-]) \subseteq \overrightarrow {{}^{ab}{}{E}}_\ell$
, as desired.
$E(G[Y^-]) \subseteq \overrightarrow {{}^{ab}{}{E}}_\ell$
, as desired.
Let
![]() $Y^-_1 \,:\!= Y^- {\setminus} \{a, b, y, z\}$
and
$Y^-_1 \,:\!= Y^- {\setminus} \{a, b, y, z\}$
and
![]() $Y^+_1 \,:\!= Y^+ {\setminus} \{a, b, y, z\}$
. Suppose that
$Y^+_1 \,:\!= Y^+ {\setminus} \{a, b, y, z\}$
. Suppose that
![]() $Y^-_1$
is an independent (or empty) set in
$Y^-_1$
is an independent (or empty) set in
![]() $G$
. Note that
$G$
. Note that
![]() $|Y^-_1 \cup Y^+_1| \ge (1- 2 \sigma )n-4$
and
$|Y^-_1 \cup Y^+_1| \ge (1- 2 \sigma )n-4$
and
![]() $\delta ^0(G) \ge \delta (G) - n \ge (3/5+\gamma ) n$
. Thus, there exist
$\delta ^0(G) \ge \delta (G) - n \ge (3/5+\gamma ) n$
. Thus, there exist
![]() $v_1,v_2,v_3,v_4 \in Y^-_1 \cup Y^+_1$
such that
$v_1,v_2,v_3,v_4 \in Y^-_1 \cup Y^+_1$
such that
![]() $abv_1v_2v_3v_4$
is a
$abv_1v_2v_3v_4$
is a
![]() $2$
-path in
$2$
-path in
![]() $G$
. Since
$G$
. Since
![]() $Y^-_1$
is an independent (or empty) set, there exists some
$Y^-_1$
is an independent (or empty) set, there exists some
![]() $i \in [3]$
such that
$i \in [3]$
such that
![]() $v_i,v_{i+1} \in Y^+_1$
. By Claim 5.13,
$v_i,v_{i+1} \in Y^+_1$
. By Claim 5.13,
![]() $v_i v_{i+1} \in E(G[Y^+]) \subseteq \overrightarrow {E^{yz}}_{12-i}$
. Therefore, there are at least
$v_i v_{i+1} \in E(G[Y^+]) \subseteq \overrightarrow {E^{yz}}_{12-i}$
. Therefore, there are at least
![]() $(\sigma n)^{8-i}$
$(\sigma n)^{8-i}$
![]() $2$
-walks of length
$2$
-walks of length
![]() $13$
in
$13$
in
![]() $G$
that start with
$G$
that start with
![]() $abv_1 \ldots v_iv_{i+1}$
and end with
$abv_1 \ldots v_iv_{i+1}$
and end with
![]() $yz$
. By a simple counting argument, one such
$yz$
. By a simple counting argument, one such
![]() $2$
-walk is in fact a
$2$
-walk is in fact a
![]() $2$
-path. Thus, the conclusion of the lemma holds in this case.
$2$
-path. Thus, the conclusion of the lemma holds in this case.
An analogous argument holds in the case when
![]() $Y^+_1$
is an independent (or empty) set in
$Y^+_1$
is an independent (or empty) set in
![]() $G$
. Thus, we may assume that neither
$G$
. Thus, we may assume that neither
![]() $Y^-_1$
nor
$Y^-_1$
nor
![]() $Y^+_1$
is an independent or empty set.
$Y^+_1$
is an independent or empty set.
Let
![]() $G' \,:\!= G {\setminus} ( X^- \cup X^+ \cup \{a, b, y, z\})=G[Y^-_1 \cup Y^+ _1]$
, so
$G' \,:\!= G {\setminus} ( X^- \cup X^+ \cup \{a, b, y, z\})=G[Y^-_1 \cup Y^+ _1]$
, so
![]() $\delta (G') \ge \delta (G) - 2 \sigma n - 4 \ge (8/5+\gamma /2) n$
. Then by applying Lemma 5.6 to
$\delta (G') \ge \delta (G) - 2 \sigma n - 4 \ge (8/5+\gamma /2) n$
. Then by applying Lemma 5.6 to
![]() $G'$
and the partition
$G'$
and the partition
![]() $\{Y^-_1, Y^+_1\}$
of
$\{Y^-_1, Y^+_1\}$
of
![]() $V(G')$
, there exists a
$V(G')$
, there exists a
![]() $2$
-path on at most
$2$
-path on at most
![]() $6$
vertices in
$6$
vertices in
![]() $G'$
that starts with an edge in
$G'$
that starts with an edge in
![]() $E(G[Y^-_1])$
and ends with an edge in
$E(G[Y^-_1])$
and ends with an edge in
![]() $E(G[Y^+_1])$
. By Claim 5.13,
$E(G[Y^+_1])$
. By Claim 5.13,
![]() $E(G[Y^-_1]) \subseteq \overrightarrow {{}^{ab}{}{E}}_9$
and
$E(G[Y^-_1]) \subseteq \overrightarrow {{}^{ab}{}{E}}_9$
and
![]() $E(G[Y^+_1]) \subseteq \overrightarrow {E^{yz}}_9$
. Combining these facts, and using an averaging argument, one obtains a
$E(G[Y^+_1]) \subseteq \overrightarrow {E^{yz}}_9$
. Combining these facts, and using an averaging argument, one obtains a
![]() $2$
-path on at most
$2$
-path on at most
![]() $20$
vertices in
$20$
vertices in
![]() $G$
that starts with
$G$
that starts with
![]() $ab$
and ends with
$ab$
and ends with
![]() $yz$
, as desired.
$yz$
, as desired.
From Lemma 5.10, we can easily deduce the following slight strengthening.
Lemma 5.14 (Connecting lemma for total degree in digraphs). Let
![]() $0 \lt 1/n \ll \gamma \lt 1$
. If
$0 \lt 1/n \ll \gamma \lt 1$
. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex digraph with
$n$
-vertex digraph with
![]() $\delta (G)\geq (8/5+\gamma )n$
, then for every pair of disjoint edges
$\delta (G)\geq (8/5+\gamma )n$
, then for every pair of disjoint edges
![]() $ab, yz \in E(G)$
and every set
$ab, yz \in E(G)$
and every set
![]() $U\subseteq V(G){\setminus} \{a,b,y,z\}$
of size at most
$U\subseteq V(G){\setminus} \{a,b,y,z\}$
of size at most
![]() $\gamma n/2$
, there exists a
$\gamma n/2$
, there exists a
![]() $2$
-path
$2$
-path
![]() $x_1x_2 \ldots x_{\ell -1}x_{\ell }$
of length
$x_1x_2 \ldots x_{\ell -1}x_{\ell }$
of length
![]() $\ell \leq 20$
in
$\ell \leq 20$
in
![]() $G {\setminus} U$
where
$G {\setminus} U$
where
![]() $x_1=a$
,
$x_1=a$
,
![]() $x_2=b$
,
$x_2=b$
,
![]() $x_{\ell -1}=y$
, and
$x_{\ell -1}=y$
, and
![]() $x_\ell =z$
.
$x_\ell =z$
.
Proof. As
![]() $\delta (G {\setminus} U)\geq (8/5 + \gamma /2)n$
, this follows immediately by applying Lemma 5.10 to
$\delta (G {\setminus} U)\geq (8/5 + \gamma /2)n$
, this follows immediately by applying Lemma 5.10 to
![]() $G{\setminus} U$
.
$G{\setminus} U$
.
6. Oriented graphs: absorbing, connecting, and almost covering lemmas for Theorem1.4
The goal of this section is to present the proofs of the absorbing, connecting, and almost covering lemmas for Theorem1.5; see Lemmas 6.7, 6.8, and 6.10.
6.1 Auxiliary lemmas for connecting and absorbing
In contrast to Lemma 5.14, our connecting lemma for oriented graphs (Lemma 6.8) does not imply the existence of a
![]() $k$
-path between every pair of
$k$
-path between every pair of
![]() $k$
-tuples
$k$
-tuples
![]() $T_1$
and
$T_1$
and
![]() $T_2$
. It will only imply the existence of such a
$T_2$
. It will only imply the existence of such a
![]() $k$
-path if
$k$
-path if
![]() $T_1$
has many common out-neighbours and
$T_1$
has many common out-neighbours and
![]() $T_2$
has many common in-neighbours. To make this precise, we introduce the following definition.
$T_2$
has many common in-neighbours. To make this precise, we introduce the following definition.
Definition 6.1.
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex oriented graph and
$n$
-vertex oriented graph and
![]() $0 \lt \delta \lt 1$
. We say that a
$0 \lt \delta \lt 1$
. We say that a
![]() $k$
-vertex tournament
$k$
-vertex tournament
![]() $T$
in
$T$
in
![]() $G$
is
$G$
is
![]() $\delta$
-out-good if
$\delta$
-out-good if
![]() $|\bigcap _{x\in V(T)}N^+_G(x)|\geq \frac {(2k-1)\delta -k+1}{k2^{2k-1}}n$
. Likewise,
$|\bigcap _{x\in V(T)}N^+_G(x)|\geq \frac {(2k-1)\delta -k+1}{k2^{2k-1}}n$
. Likewise,
![]() $T$
is
$T$
is
![]() $\delta$
-in-good if
$\delta$
-in-good if
![]() $|\bigcap _{x\in V(T)}N^-_G(x)|\geq \frac {(2k-1)\delta -k+1}{k2^{2k-1}}n$
. If a
$|\bigcap _{x\in V(T)}N^-_G(x)|\geq \frac {(2k-1)\delta -k+1}{k2^{2k-1}}n$
. If a
![]() $k$
-path
$k$
-path
![]() $P$
starts with a
$P$
starts with a
![]() $\delta$
-in-good tournament on
$\delta$
-in-good tournament on
![]() $k$
vertices and ends in a
$k$
vertices and ends in a
![]() $\delta$
-out-good tournament on
$\delta$
-out-good tournament on
![]() $k$
vertices, we say that
$k$
vertices, we say that
![]() $P$
is a
$P$
is a
![]() $\delta$
-good
$\delta$
-good
![]() $k$
-path.
$k$
-path.
Note that Definition 6.1 is only useful when
![]() $\delta$
is reasonably large, since for
$\delta$
is reasonably large, since for
![]() $0\lt \delta \leq (k-1)/(2k-1)$
, the common out- and in-neighbourhood conditions here do not even guarantee a single common out- or in-neighbour.
$0\lt \delta \leq (k-1)/(2k-1)$
, the common out- and in-neighbourhood conditions here do not even guarantee a single common out- or in-neighbour.
The next lemma states that every large enough tournament in a dense oriented graph contains a
![]() $\delta$
-in/out-good subtournament on
$\delta$
-in/out-good subtournament on
![]() $k$
vertices.
$k$
vertices.
Lemma 6.2.
Let
![]() $k\geq 2$
and let
$k\geq 2$
and let
![]() $G$
be a sufficiently large
$G$
be a sufficiently large
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
![]() $\delta ^0(G) = \delta n \gt \frac {(k-1)n}{2k-1}$
. Let
$\delta ^0(G) = \delta n \gt \frac {(k-1)n}{2k-1}$
. Let
![]() $T$
be a
$T$
be a
![]() $(2k-1)$
-vertex tournament in
$(2k-1)$
-vertex tournament in
![]() $G$
. Then
$G$
. Then
![]() $T$
contains a
$T$
contains a
![]() $\delta$
-out-good tournament and a
$\delta$
-out-good tournament and a
![]() $\delta$
-in-good tournament, each on
$\delta$
-in-good tournament, each on
![]() $k$
vertices.
$k$
vertices.
Proof. Let
![]() $X \,:\!= V(T)$
,
$X \,:\!= V(T)$
,
![]() $Y \,:\!= \{v\in V(G)\; :\; d^-_G(v,X)\leq k-1\}$
, and
$Y \,:\!= \{v\in V(G)\; :\; d^-_G(v,X)\leq k-1\}$
, and
![]() $Z \,:\!= \{v\in V(G)\; :\; d^-_G(v,X)\geq k\}$
. We have
$Z \,:\!= \{v\in V(G)\; :\; d^-_G(v,X)\geq k\}$
. We have
so
Thus, there exists a
![]() $k$
-set
$k$
-set
![]() $X'\subseteq X$
such that
$X'\subseteq X$
such that
 \begin{align*} \left |\bigcap _{x\in X'}N^+_G(x) \right | & \geq \frac {|Z|}{\binom {2k-1}{k}} \geq \frac { ( (2k-1)\delta -k+1)n-(2k-1)^2}{\binom {2k-1}{k}k} \geq \frac {(2k-1)\delta -k+1}{k2^{2k-1}}n, \end{align*}
\begin{align*} \left |\bigcap _{x\in X'}N^+_G(x) \right | & \geq \frac {|Z|}{\binom {2k-1}{k}} \geq \frac { ( (2k-1)\delta -k+1)n-(2k-1)^2}{\binom {2k-1}{k}k} \geq \frac {(2k-1)\delta -k+1}{k2^{2k-1}}n, \end{align*}
where the last inequality follows as
![]() $n$
is sufficiently large. Therefore,
$n$
is sufficiently large. Therefore,
![]() $X'$
induces a
$X'$
induces a
![]() $\delta$
-out-good tournament on
$\delta$
-out-good tournament on
![]() $k$
vertices. The proof for
$k$
vertices. The proof for
![]() $\delta$
-in-good tournaments is analogous.
$\delta$
-in-good tournaments is analogous.
The following lemma states that given an oriented graph
![]() $G$
with large minimum semi-degree, for every two large disjoint sets of vertices
$G$
with large minimum semi-degree, for every two large disjoint sets of vertices
![]() $A$
and
$A$
and
![]() $B$
, there are many edges from
$B$
, there are many edges from
![]() $A$
to
$A$
to
![]() $B$
.
$B$
.
Lemma 6.3 (Crossing edges between large sets). Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
![]() $\delta ^0(G)\geq \delta n \geq \frac {2n}{5}$
. Then, for any disjoint sets
$\delta ^0(G)\geq \delta n \geq \frac {2n}{5}$
. Then, for any disjoint sets
![]() $A,B\subseteq V(G)$
, we have
$A,B\subseteq V(G)$
, we have
In particular, if
![]() $|A|\geq |B| \geq \delta n$
, then
$|A|\geq |B| \geq \delta n$
, then
Proof. We have
 \begin{align*} e_G(A,B)&\geq \sum _{v\in A} \left ( d^+_G(v) - d^+_G(v, A) - (n-|A|-|B|) \right ) \geq |A|\delta n-e(G[A])-|A|(n-|A|-|B|)\\ &\geq |A|\delta n-\frac {|A|^2}{2}-|A|(n-|A|-|B|) = |A|\left (\frac {|A|}{2}+|B|-(1-\delta )n\right ). \end{align*}
\begin{align*} e_G(A,B)&\geq \sum _{v\in A} \left ( d^+_G(v) - d^+_G(v, A) - (n-|A|-|B|) \right ) \geq |A|\delta n-e(G[A])-|A|(n-|A|-|B|)\\ &\geq |A|\delta n-\frac {|A|^2}{2}-|A|(n-|A|-|B|) = |A|\left (\frac {|A|}{2}+|B|-(1-\delta )n\right ). \end{align*}
When
![]() $|A|\geq |B| \geq \delta n$
, the desired inequality follows easily since
$|A|\geq |B| \geq \delta n$
, the desired inequality follows easily since
Recall that
![]() $\vec {r}(k)$
and
$\vec {r}(k)$
and
![]() $ \vec {tr}(k)$
are defined at the beginning of Section 3.2. The following result will allow us to find large transitive tournaments in oriented graphs with large minimum semi-degree.
$ \vec {tr}(k)$
are defined at the beginning of Section 3.2. The following result will allow us to find large transitive tournaments in oriented graphs with large minimum semi-degree.
Lemma 6.4.
Let
![]() $k \geq 2$
and let
$k \geq 2$
and let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
![]() $\delta ^0(G)=\delta n$
.
$\delta ^0(G)=\delta n$
.
-
(i) If
 $X\subseteq V(G)$
with
$X\subseteq V(G)$
with
 $|X|\gt (\vec {r}(k)-1)(1-2\delta )n$
, then
$|X|\gt (\vec {r}(k)-1)(1-2\delta )n$
, then
 $G[X]$
contains a copy of
$G[X]$
contains a copy of
 $\vec {T}_k$
.
$\vec {T}_k$
. -
(ii) If
 $X\subseteq V(G)$
with
$X\subseteq V(G)$
with
 $|X|\geq \vec {tr}(k)(1-2\delta )n$
and
$|X|\geq \vec {tr}(k)(1-2\delta )n$
and
 $|X|$
divisible by
$|X|$
divisible by
 $k$
, then
$k$
, then
 $G[X]$
has a
$G[X]$
has a
 $\vec {T}_k$
-factor.
$\vec {T}_k$
-factor.
-
(iii) If
 $X\subseteq V(G)$
with
$X\subseteq V(G)$
with
 $|X|\geq 3^k(1-2\delta )n$
, then
$|X|\geq 3^k(1-2\delta )n$
, then
 $G[X]$
contains at least
$G[X]$
contains at least
 $\left (\frac {|X|}{3^{k}}\right )^k$
copies of
$\left (\frac {|X|}{3^{k}}\right )^k$
copies of
 $\vec {T}_k$
.
$\vec {T}_k$
.
Proof. Note
![]() $|X|\gt (\vec {r}(k)-1)(1-2\delta )n$
implies that
$|X|\gt (\vec {r}(k)-1)(1-2\delta )n$
implies that
![]() $\delta (G[X])\geq |X|-(1-2\delta )n\gt \frac {\vec {r}(k)-2}{\vec {r}(k)-1}|X|$
. Thus, by Turán’s theorem, there exists a tournament
$\delta (G[X])\geq |X|-(1-2\delta )n\gt \frac {\vec {r}(k)-2}{\vec {r}(k)-1}|X|$
. Thus, by Turán’s theorem, there exists a tournament
![]() $T$
on
$T$
on
![]() $\vec {r}(k)$
vertices in
$\vec {r}(k)$
vertices in
![]() $G[X]$
; by definition of
$G[X]$
; by definition of
![]() $\vec {r}(k)$
,
$\vec {r}(k)$
,
![]() $T$
contains a copy of
$T$
contains a copy of
![]() $\vec {T}_k$
.
$\vec {T}_k$
.
Similarly,
![]() $|X|\geq \vec {tr}(k)(1-2\delta )n$
implies that
$|X|\geq \vec {tr}(k)(1-2\delta )n$
implies that
![]() $\delta (G[X])\geq |X|-(1-2\delta )n\geq \frac {\vec {tr}(k)-1}{\vec {tr}(k)}|X|$
. By [Reference Treglown35, Proposition 9] (itself a simple corollary of the Hajnal–Szemerédi theorem),
$\delta (G[X])\geq |X|-(1-2\delta )n\geq \frac {\vec {tr}(k)-1}{\vec {tr}(k)}|X|$
. By [Reference Treglown35, Proposition 9] (itself a simple corollary of the Hajnal–Szemerédi theorem),
![]() $G[X]$
contains a
$G[X]$
contains a
![]() $\vec {T}_k$
-factor.
$\vec {T}_k$
-factor.
For (iii), note
![]() $|X|\geq 3^k(1-2\delta )n$
implies that
$|X|\geq 3^k(1-2\delta )n$
implies that
![]() $\delta (G[X])\geq |X|-(1-2\delta )n\geq (1-\frac {1}{3^k})|X|$
. The idea is to greedily construct a
$\delta (G[X])\geq |X|-(1-2\delta )n\geq (1-\frac {1}{3^k})|X|$
. The idea is to greedily construct a
![]() $\vec {T}_k$
in
$\vec {T}_k$
in
![]() $G[X]$
by choosing an arbitrary vertex and noting that at least half of its incident edges have the same direction. Then look inside that neighbourhood, choose an arbitrary vertex and repeat. More precisely, for all
$G[X]$
by choosing an arbitrary vertex and noting that at least half of its incident edges have the same direction. Then look inside that neighbourhood, choose an arbitrary vertex and repeat. More precisely, for all
![]() $0\leq i\leq k-2$
we have
$0\leq i\leq k-2$
we have
![]() $\frac {\frac {|X|}{3^i}-\frac {|X|}{3^k}}{2}\geq \frac {|X|}{3^{i+1}}$
, and thus this greedy process produces at least
$\frac {\frac {|X|}{3^i}-\frac {|X|}{3^k}}{2}\geq \frac {|X|}{3^{i+1}}$
, and thus this greedy process produces at least
![]() $\prod _{i=0}^{k-1}\frac {|X|}{3^i}=\frac {|X|^k}{3^{k(k-1)/2}}$
copies of
$\prod _{i=0}^{k-1}\frac {|X|}{3^i}=\frac {|X|^k}{3^{k(k-1)/2}}$
copies of
![]() $\vec {T}_k$
in
$\vec {T}_k$
in
![]() $G[X]$
; however, up to
$G[X]$
; however, up to
![]() $2^k$
different options for this greedy process give rise to the same copy of
$2^k$
different options for this greedy process give rise to the same copy of
![]() $\vec {T}_k$
. Therefore, we obtain at least
$\vec {T}_k$
. Therefore, we obtain at least
![]() $\frac {1}{2^k\cdot 3^{k(k-1)/2}}|X|^k\geq \frac {1}{3^{k^2}}|X|^k$
copies of
$\frac {1}{2^k\cdot 3^{k(k-1)/2}}|X|^k\geq \frac {1}{3^{k^2}}|X|^k$
copies of
![]() $\vec {T}_k$
in
$\vec {T}_k$
in
![]() $G[X]$
.
$G[X]$
.
The following lemma is an amalgamation of [Reference Draganić, Munhá Correia and Sudakov10, Lemma 2.9] and [Reference Fox and Sudakov20, Lemma 6.3]. Since the statement is slightly different, for completeness, we rewrite their proof tailored to our statement.
Lemma 6.5 (Dependent random choice variant). Let
![]() $k \in \mathbb N$
,
$k \in \mathbb N$
,
![]() $0\lt d\leq 1$
, and define
$0\lt d\leq 1$
, and define
![]() $c \,:\!= d^k/\sqrt [k]{2}$
. Let
$c \,:\!= d^k/\sqrt [k]{2}$
. Let
![]() $G=(A,B)$
be a bipartite graph with
$G=(A,B)$
be a bipartite graph with
![]() $e(G)\geq d |A||B|$
. For all
$e(G)\geq d |A||B|$
. For all
![]() $0\lt {\varepsilon }\lt 1$
, there exists
$0\lt {\varepsilon }\lt 1$
, there exists
![]() $U\subseteq A$
with
$U\subseteq A$
with
![]() $|U| \geq c |A|$
such that all but at most
$|U| \geq c |A|$
such that all but at most
![]() $\left ({\varepsilon } |U|\right )^k$
of the
$\left ({\varepsilon } |U|\right )^k$
of the
![]() $k$
-tuples in
$k$
-tuples in
![]() $U$
have at least
$U$
have at least
![]() ${\varepsilon } c |B|$
common neighbours in
${\varepsilon } c |B|$
common neighbours in
![]() $B$
.
$B$
.
Proof. Let
![]() $S$
be a subset of
$S$
be a subset of
![]() $k$
random vertices, chosen uniformly from
$k$
random vertices, chosen uniformly from
![]() $B$
with repetition. Let
$B$
with repetition. Let
![]() $U$
denote the set of common neighbours of
$U$
denote the set of common neighbours of
![]() $S$
in
$S$
in
![]() $A$
. Note that linearity of expectation and Jensen’s inequality imply
$A$
. Note that linearity of expectation and Jensen’s inequality imply
![]() $\mathbb{E}[|U|] = \sum _{v\in A} \left (\frac {d_G(v)}{|B|}\right )^k\geq d^k |A| = 2^{1/k} c |A|.$
$\mathbb{E}[|U|] = \sum _{v\in A} \left (\frac {d_G(v)}{|B|}\right )^k\geq d^k |A| = 2^{1/k} c |A|.$
Let
![]() $Y$
denote the number of
$Y$
denote the number of
![]() $k$
-tuples in
$k$
-tuples in
![]() $U$
with fewer than
$U$
with fewer than
![]() $m \,:\!= {\varepsilon } c |B|$
common neighbours in
$m \,:\!= {\varepsilon } c |B|$
common neighbours in
![]() $B$
. Note that, by linearity of expectation,
$B$
. Note that, by linearity of expectation,
By the previous two inequalities and another application of Jensen’s inequality, we have
which, by linearity of expectation, implies
Thus, there is a choice of
![]() $S$
for which
$S$
for which
![]() $Y \leq \left ({\varepsilon } |U|\right )^k$
and for which
$Y \leq \left ({\varepsilon } |U|\right )^k$
and for which
![]() $ ({\varepsilon } |U|)^k \ge \left ({\varepsilon } c |A| \right )^k$
, and so
$ ({\varepsilon } |U|)^k \ge \left ({\varepsilon } c |A| \right )^k$
, and so
![]() $|U|\geq c |A|$
.
$|U|\geq c |A|$
.
6.2 The absorbing lemma
In this section we will use a very slightly different absorber compared to that used in Section 5.2.
Definition 6.6.
Given a digraph
![]() $G$
and
$G$
and
![]() $x\in V(G)$
, we say that a
$x\in V(G)$
, we say that a
![]() $k$
-path
$k$
-path
![]() $u_1\ldots u_kv_1\ldots v_k$
on
$u_1\ldots u_kv_1\ldots v_k$
on
![]() $2k$
vertices in
$2k$
vertices in
![]() $G$
is a
$G$
is a
![]() $k$
-absorber for
$k$
-absorber for
![]() $x$
if
$x$
if
![]() $u_1\ldots u_kxv_1\ldots v_k$
is a
$u_1\ldots u_kxv_1\ldots v_k$
is a
![]() $k$
-path in
$k$
-path in
![]() $G$
as well. We say that a
$G$
as well. We say that a
![]() $k$
-path
$k$
-path
![]() $u_1\ldots u_{2k}v_1\ldots v_{2k}$
on
$u_1\ldots u_{2k}v_1\ldots v_{2k}$
on
![]() $4k$
vertices in
$4k$
vertices in
![]() $G$
is a stretched
$G$
is a stretched
![]() $k$
-absorber for
$k$
-absorber for
![]() $x$
if
$x$
if
![]() $u_1\ldots u_{2k}xv_1\ldots v_{2k}$
is a
$u_1\ldots u_{2k}xv_1\ldots v_{2k}$
is a
![]() $k$
-path in
$k$
-path in
![]() $G$
as well.
$G$
as well.
Note that we will only use the notion of a stretched
![]() $k$
-absorber in the proof of Theorem1.5 in Section 7.1.
$k$
-absorber in the proof of Theorem1.5 in Section 7.1.
Lemma 6.7.
Let
![]() $0\lt 1/n \ll \xi \ll 1/k \le 1/2$
. If
$0\lt 1/n \ll \xi \ll 1/k \le 1/2$
. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
![]() $\delta ^0(G) =\delta n\ge \left (\frac {1}{2}-\frac {1}{4\cdot 3^{3k+2}}\right )n$
, then every
$\delta ^0(G) =\delta n\ge \left (\frac {1}{2}-\frac {1}{4\cdot 3^{3k+2}}\right )n$
, then every
![]() $x\in V(G)$
has at least
$x\in V(G)$
has at least
![]() $\xi n^{2k}$
$\xi n^{2k}$
![]() $k$
-absorbers in
$k$
-absorbers in
![]() $G$
.
$G$
.
Proof. Given any
![]() $x \in V(G)$
, let
$x \in V(G)$
, let
![]() $A\subseteq N^{-}_G(x)$
and
$A\subseteq N^{-}_G(x)$
and
![]() $B\subseteq N^+_G(x)$
be both of size
$B\subseteq N^+_G(x)$
be both of size
![]() $\delta n$
. By Lemma 6.3, we have
$\delta n$
. By Lemma 6.3, we have
Let
![]() $U\subseteq A$
be the set obtained by applying Lemma 6.5 to the underlying graph of
$U\subseteq A$
be the set obtained by applying Lemma 6.5 to the underlying graph of
![]() $G[A,B]$
and with parameters
$G[A,B]$
and with parameters
In particular, it holds that
Thus, Lemma 6.4(iii) yields at least
![]() $(|U|/3^k)^k$
copies of
$(|U|/3^k)^k$
copies of
![]() $\vec {T}_k$
in
$\vec {T}_k$
in
![]() $G[U]$
.
$G[U]$
.
Due to our application of Lemma 6.5, all but at most
![]() $(|U|/3^{k+1})^{k}$
of the
$(|U|/3^{k+1})^{k}$
of the
![]() $k$
-tuples in
$k$
-tuples in
![]() $U$
have at least
$U$
have at least
![]() $\varepsilon d^k|B|/2 =|B|/(2\cdot 3^{2k+1})$
common out-neighbours in
$\varepsilon d^k|B|/2 =|B|/(2\cdot 3^{2k+1})$
common out-neighbours in
![]() $B$
. Hence, there are at least
$B$
. Hence, there are at least
![]() $(3^{-k^2}- 3^{-k^2-k})|U|^k\gt (3^{-k^2-1})|U|^k$
copies
$(3^{-k^2}- 3^{-k^2-k})|U|^k\gt (3^{-k^2-1})|U|^k$
copies
![]() $T_1$
of
$T_1$
of
![]() $\vec {T}_k$
in
$\vec {T}_k$
in
![]() $G[U]$
such that the vertices in
$G[U]$
such that the vertices in
![]() $T_1$
have at least
$T_1$
have at least
![]() $|B|/(2\cdot 3^{2k+1})$
common out-neighbours in
$|B|/(2\cdot 3^{2k+1})$
common out-neighbours in
![]() $B$
.
$B$
.
Fix one such tournament
![]() $T_1\subseteq G[U]$
and observe that
$T_1\subseteq G[U]$
and observe that
 \begin{align*} \left | \bigcap _{v \in V(T_1)} N^{+}_G(v, B) \right | \geq \frac {|B|}{2\cdot 3^{2k+1}} \geq \frac {n}{2\cdot 3^{2k+2}} \geq 3^k(1-2\delta ) n . \end{align*}
\begin{align*} \left | \bigcap _{v \in V(T_1)} N^{+}_G(v, B) \right | \geq \frac {|B|}{2\cdot 3^{2k+1}} \geq \frac {n}{2\cdot 3^{2k+2}} \geq 3^k(1-2\delta ) n . \end{align*}
An application of Lemma 6.4(iii) yields at least
![]() $(|\bigcap _{v \in V(T_1)} N^{+}_G(v,B)|/3^k)^k\geq n^k /(3^{3k(k+1)} )$
copies
$(|\bigcap _{v \in V(T_1)} N^{+}_G(v,B)|/3^k)^k\geq n^k /(3^{3k(k+1)} )$
copies
![]() $T_2$
of
$T_2$
of
![]() $\vec {T}_k$
contained in
$\vec {T}_k$
contained in
![]() $\bigcap _{v \in V(T_1)} N^{+}_G(v,B)$
. Fix one such tournament
$\bigcap _{v \in V(T_1)} N^{+}_G(v,B)$
. Fix one such tournament
![]() $T_2$
. As
$T_2$
. As
![]() $V(T_1)\subseteq U \subseteq A \subseteq N^- _G(x)$
and
$V(T_1)\subseteq U \subseteq A \subseteq N^- _G(x)$
and
![]() $V(T_2)\subseteq B \subseteq N^+ _G(x)$
, we can let
$V(T_2)\subseteq B \subseteq N^+ _G(x)$
, we can let
![]() $T_1=:u_1\ldots u_k$
and
$T_1=:u_1\ldots u_k$
and
![]() $T_2=:v_1\ldots v_k$
so that
$T_2=:v_1\ldots v_k$
so that
![]() $u_1\ldots u_kv_1\ldots v_k$
is a
$u_1\ldots u_kv_1\ldots v_k$
is a
![]() $k$
-absorber for
$k$
-absorber for
![]() $x$
.
$x$
.
Note that there are more that
![]() $(3^{-k^2-1})|U|^k\geq (3^{-k^2-1})\frac {d^{k^2}}{2^k}|A|^k\geq \frac {n^k}{3^{3k^2+1}}$
choices for
$(3^{-k^2-1})|U|^k\geq (3^{-k^2-1})\frac {d^{k^2}}{2^k}|A|^k\geq \frac {n^k}{3^{3k^2+1}}$
choices for
![]() $T_1$
and, given a fixed choice of
$T_1$
and, given a fixed choice of
![]() $T_1$
, at least
$T_1$
, at least
![]() $n^k /(3^{3k(k+1)} )$
choices for
$n^k /(3^{3k(k+1)} )$
choices for
![]() $T_2$
. Thus, in total we obtain at least
$T_2$
. Thus, in total we obtain at least
![]() $k$
-absorbers for
$k$
-absorbers for
![]() $x$
, as desired.
$x$
, as desired.
6.3 The connecting lemma
The following lemma allows us to connect a
![]() $\delta$
-out-good copy of
$\delta$
-out-good copy of
![]() $\vec {T}_{k}$
to a
$\vec {T}_{k}$
to a
![]() $\delta$
-in-good copy of
$\delta$
-in-good copy of
![]() $\vec {T}_{k}$
by a short
$\vec {T}_{k}$
by a short
![]() $k$
-path that avoids any small set of vertices.
$k$
-path that avoids any small set of vertices.
Lemma 6.8 (Connecting an out-good
![]() $\vec {T}_{k}$
to an in-good
$\vec {T}_{k}$
to an in-good
![]() $\vec {T}_{k}$
). Let
$\vec {T}_{k}$
). Let
![]() $0\lt 1/n \ll \zeta \ll 1/k \leq 1/2$
. Let
$0\lt 1/n \ll \zeta \ll 1/k \leq 1/2$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
![]() $\delta ^0(G) \ge \left (\frac {1}{2}-\frac {1}{ 3^{18k}} \right )n$
. Set
$\delta ^0(G) \ge \left (\frac {1}{2}-\frac {1}{ 3^{18k}} \right )n$
. Set
![]() $\delta \,:\!= \left (\frac {1}{2}-\frac {1}{2\cdot 3^{17k}} \right )$
. Given any pair of vertex-disjoint
$\delta \,:\!= \left (\frac {1}{2}-\frac {1}{2\cdot 3^{17k}} \right )$
. Given any pair of vertex-disjoint
![]() $\delta$
-out-good
$\delta$
-out-good
![]() $T^+$
and
$T^+$
and
![]() $\delta$
-in-good
$\delta$
-in-good
![]() $T^-$
copies of
$T^-$
copies of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G$
, and any set of vertices
$G$
, and any set of vertices
![]() $U\subseteq V(G){\setminus} (V(T^{+}) \cup V(T^-))$
of size at most
$U\subseteq V(G){\setminus} (V(T^{+}) \cup V(T^-))$
of size at most
![]() $\zeta n$
, there exists
$\zeta n$
, there exists
![]() $\ell \in \{3,4\}$
such that there is a
$\ell \in \{3,4\}$
such that there is a
![]() $k$
-path from
$k$
-path from
![]() $T^+$
to
$T^+$
to
![]() $T^-$
on
$T^-$
on
![]() $k(\ell +2)$
vertices in
$k(\ell +2)$
vertices in
![]() $G{\setminus} U$
.
$G{\setminus} U$
.
Proof. Set
![]() $\alpha \,:\!= 1/27$
and
$\alpha \,:\!= 1/27$
and
![]() $\tau \,:\!= {3^{-6(k+1)}}$
. Note that
$\tau \,:\!= {3^{-6(k+1)}}$
. Note that
Take
![]() $G$
,
$G$
,
![]() $T^{+}$
,
$T^{+}$
,
![]() $T^{-}$
, and
$T^{-}$
, and
![]() $U$
to be as in the statement of the lemma. As
$U$
to be as in the statement of the lemma. As
![]() $\zeta \ll 1/k$
we have
$\zeta \ll 1/k$
we have
![]() $\delta ^0(G{\setminus} U)\geq \delta n$
.
$\delta ^0(G{\setminus} U)\geq \delta n$
.
Set
![]() $G' \,:\!= G{\setminus} U$
and let
$G' \,:\!= G{\setminus} U$
and let
 \begin{align*} A_1 & \,:\!= \left (\bigcap _{v \in V(T^+)} N^+_{G'}(v) \right ) {\setminus} V(T^-), & B_1 & \,:\!= \left (\bigcap _{v \in V(T^-)} N^-_{G'}(v) \right ) {\setminus} V(T^{+}) , \end{align*}
\begin{align*} A_1 & \,:\!= \left (\bigcap _{v \in V(T^+)} N^+_{G'}(v) \right ) {\setminus} V(T^-), & B_1 & \,:\!= \left (\bigcap _{v \in V(T^-)} N^-_{G'}(v) \right ) {\setminus} V(T^{+}) , \end{align*}
and
So
![]() $A_1, A_2, B_1$
and
$A_1, A_2, B_1$
and
![]() $B_2$
are all disjoint from
$B_2$
are all disjoint from
![]() $T^+$
and
$T^+$
and
![]() $T^-$
. As
$T^-$
. As
![]() $T^+$
is
$T^+$
is
![]() $\delta$
-out-good in
$\delta$
-out-good in
![]() $G$
, we have that
$G$
, we have that
Furthermore,
Therefore, we have
![]() $|A_2|\geq \frac {\delta -\alpha }{1-\alpha }n-\frac {2k}{1-\alpha } \geq \tfrac {4}{9}n$
. Analogous calculations for
$|A_2|\geq \frac {\delta -\alpha }{1-\alpha }n-\frac {2k}{1-\alpha } \geq \tfrac {4}{9}n$
. Analogous calculations for
![]() $|B_1|$
and
$|B_1|$
and
![]() $|B_2|$
imply that
$|B_2|$
imply that
We will split into two cases depending on the size of
![]() $A_2 \cap B_2$
. First, we prove the following claim.
$A_2 \cap B_2$
. First, we prove the following claim.
Claim 6.9.
Let
![]() $Y,Z \subseteq V({G'})$
be such that
$Y,Z \subseteq V({G'})$
be such that
![]() $|Y|\geq \tau n$
and
$|Y|\geq \tau n$
and
![]() $d^+_{G'}(y,Z) \ge \alpha |Z|$
for all
$d^+_{G'}(y,Z) \ge \alpha |Z|$
for all
![]() $y \in Y$
. Then there is a copy
$y \in Y$
. Then there is a copy
![]() $T$
of
$T$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() ${G'}[Y]$
such that
${G'}[Y]$
such that
 \begin{align*} \left |\bigcap _{v \in V(T) } N^+_{G'}(v, Z) \right | \geq \frac {\alpha ^{2k}}{16}|Z|\, . \end{align*}
\begin{align*} \left |\bigcap _{v \in V(T) } N^+_{G'}(v, Z) \right | \geq \frac {\alpha ^{2k}}{16}|Z|\, . \end{align*}
Moreover, if there exists
![]() $X \subseteq V({G'})$
such that
$X \subseteq V({G'})$
such that
![]() $e_{G'}(X,Y) \geq \alpha |X||Y|$
, then we may further assume that
$e_{G'}(X,Y) \geq \alpha |X||Y|$
, then we may further assume that
 \begin{align*} \left |\bigcap _{v \in V(T) } N^-_{G'}(v, X) \right | \geq \frac {\alpha ^{2k}}{16}|X|\, . \end{align*}
\begin{align*} \left |\bigcap _{v \in V(T) } N^-_{G'}(v, X) \right | \geq \frac {\alpha ^{2k}}{16}|X|\, . \end{align*}
Note that in this claim,
![]() $X$
,
$X$
,
![]() $Y$
and
$Y$
and
![]() $Z$
are not necessarily disjoint.
$Z$
are not necessarily disjoint.
Proof. We shall apply Lemma 6.5 with
![]() $\alpha$
playing the role of
$\alpha$
playing the role of
![]() $d$
and
$d$
and
![]() $\varepsilon \,:\!= \alpha ^k/(4\sqrt [k]{4})$
, and so we set
$\varepsilon \,:\!= \alpha ^k/(4\sqrt [k]{4})$
, and so we set
![]() $c \,:\!= \alpha ^k/\sqrt [k]{2}$
. If we are not in the moreover case of the claim, then we set
$c \,:\!= \alpha ^k/\sqrt [k]{2}$
. If we are not in the moreover case of the claim, then we set
![]() $W \,:\!= Y$
. In the moreover case, we apply Lemma 6.5 to the bipartite graph
$W \,:\!= Y$
. In the moreover case, we apply Lemma 6.5 to the bipartite graph
![]() $H$
which has vertex classes
$H$
which has vertex classes
![]() $X$
and
$X$
and
![]() $Y$
and an edge between
$Y$
and an edge between
![]() $x \in X$
and
$x \in X$
and
![]() $y \in Y$
precisely if the directed edge
$y \in Y$
precisely if the directed edge
![]() $xy$
is present in
$xy$
is present in
![]() $G'$
. Thus, we obtain a set
$G'$
. Thus, we obtain a set
![]() $W\subseteq Y$
such that
$W\subseteq Y$
such that
![]() $|W| \ge c |Y|$
and in
$|W| \ge c |Y|$
and in
![]() $G'$
all but at most
$G'$
all but at most
![]() $(\varepsilon |W|)^k$
$(\varepsilon |W|)^k$
![]() $k$
-tuples in
$k$
-tuples in
![]() $W$
have at least
$W$
have at least
![]() $\varepsilon c |X|$
common in-neighbours in
$\varepsilon c |X|$
common in-neighbours in
![]() $X$
.
$X$
.
Next, we define
![]() $H'$
to be the bipartite graph which has vertex classes
$H'$
to be the bipartite graph which has vertex classes
![]() $W$
and
$W$
and
![]() $Z$
and an edge between
$Z$
and an edge between
![]() $w \in W$
and
$w \in W$
and
![]() $z \in Z$
precisely if the directed edge
$z \in Z$
precisely if the directed edge
![]() $wz$
is present in
$wz$
is present in
![]() $G'$
. Since
$G'$
. Since
![]() $W \subseteq Y$
, we have
$W \subseteq Y$
, we have
![]() $e(H') \ge \alpha |W||Z|$
. So applying Lemma 6.5 to
$e(H') \ge \alpha |W||Z|$
. So applying Lemma 6.5 to
![]() $H'$
, we obtain a subset
$H'$
, we obtain a subset
![]() $\widetilde W\subseteq W$
, where
$\widetilde W\subseteq W$
, where
and in
![]() $G'$
all but at most
$G'$
all but at most
![]() $(\varepsilon |\widetilde W|)^k \leq (\varepsilon |W|)^k$
$(\varepsilon |\widetilde W|)^k \leq (\varepsilon |W|)^k$
![]() $k$
-tuples in
$k$
-tuples in
![]() $\widetilde W$
have at least
$\widetilde W$
have at least
![]() $\varepsilon c |Z|$
common out-neighbours in
$\varepsilon c |Z|$
common out-neighbours in
![]() $Z$
.
$Z$
.
Lemma 6.4 and (6.3) imply that there are at least
![]() $(|\widetilde W|/3)^k \geq c^k |W|^k/3^k \gt 2(\varepsilon |W|)^k$
copies
$(|\widetilde W|/3)^k \geq c^k |W|^k/3^k \gt 2(\varepsilon |W|)^k$
copies
![]() $T$
of
$T$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[\widetilde W]$
. Recalling that we took
$G'[\widetilde W]$
. Recalling that we took
![]() $\varepsilon =\alpha ^k/(4\sqrt [k]{4})$
and
$\varepsilon =\alpha ^k/(4\sqrt [k]{4})$
and
![]() $c=\alpha ^k/\sqrt [k]{2}$
, we obtain one such
$c=\alpha ^k/\sqrt [k]{2}$
, we obtain one such
![]() $T$
with
$T$
with
 \begin{align*} \left |\bigcap _{v \in V(T) } N^+_{G'}(v, Z) \right | \geq \varepsilon c |Z| \geq \frac {\alpha ^{2k}}{16}|Z| \end{align*}
\begin{align*} \left |\bigcap _{v \in V(T) } N^+_{G'}(v, Z) \right | \geq \varepsilon c |Z| \geq \frac {\alpha ^{2k}}{16}|Z| \end{align*}
and, in the moreover case
 \begin{align*} \left |\bigcap _{v \in V(T) } N^-_{G'}(v , X )\right | \geq \frac {\alpha ^{2k}}{16}|X| , \end{align*}
\begin{align*} \left |\bigcap _{v \in V(T) } N^-_{G'}(v , X )\right | \geq \frac {\alpha ^{2k}}{16}|X| , \end{align*}
as required.
We first assume that
![]() $|A_2 \cap B_2| \le \tau n$
. Let
$|A_2 \cap B_2| \le \tau n$
. Let
![]() $A_2' \,:\!= A_2 {\setminus} B_2$
and
$A_2' \,:\!= A_2 {\setminus} B_2$
and
![]() $B_2' \,:\!= B_2 {\setminus} A_2$
; so
$B_2' \,:\!= B_2 {\setminus} A_2$
; so
By Lemma 6.3 (with
![]() $19/45$
playing the role of
$19/45$
playing the role of
![]() $\delta$
), we have
$\delta$
), we have
By Claim 6.9 with
![]() $A_2',B_2',B_1$
playing roles of
$A_2',B_2',B_1$
playing roles of
![]() $X,Y,Z$
, we obtain a copy
$X,Y,Z$
, we obtain a copy
![]() $T_{B_2}$
of
$T_{B_2}$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[B'_2] \subseteq G'[B_2]$
such that
$G'[B'_2] \subseteq G'[B_2]$
such that
 \begin{align*} \left |\bigcap _{v \in V(T_{B_2}) } N^+_{G'}(v, B_1 )\right | & \geq \frac { \alpha ^{2k}}{16}|B_1| \stackrel {({\hbox{6.2}})}{\ge } \frac { \alpha ^{2k}}{16 \cdot 8^k}n \stackrel {({\hbox{6.1}})}{\ge } 3^k(1-2 \delta )n \, \text{ and }\\ \left |\bigcap _{v \in V(T_{B_2}) } N^-_{G'}(v, A_2' )\right | &\geq \frac {\alpha ^{2k}}{16}|A_2'| \stackrel {({\hbox{6.4}})}{\ge } \tau n\, . \end{align*}
\begin{align*} \left |\bigcap _{v \in V(T_{B_2}) } N^+_{G'}(v, B_1 )\right | & \geq \frac { \alpha ^{2k}}{16}|B_1| \stackrel {({\hbox{6.2}})}{\ge } \frac { \alpha ^{2k}}{16 \cdot 8^k}n \stackrel {({\hbox{6.1}})}{\ge } 3^k(1-2 \delta )n \, \text{ and }\\ \left |\bigcap _{v \in V(T_{B_2}) } N^-_{G'}(v, A_2' )\right | &\geq \frac {\alpha ^{2k}}{16}|A_2'| \stackrel {({\hbox{6.4}})}{\ge } \tau n\, . \end{align*}
By applying Claim 6.9 with
![]() $\bigcap _{v \in V(T_{B_2}) } N^-_{G'}(v, A_2' )$
and
$\bigcap _{v \in V(T_{B_2}) } N^-_{G'}(v, A_2' )$
and
![]() $ A_1$
playing the roles of
$ A_1$
playing the roles of
![]() $Y$
and
$Y$
and
![]() $ Z$
(and with the orientations of each edge reversed), we obtain a copy
$ Z$
(and with the orientations of each edge reversed), we obtain a copy
![]() $T_{A_2}$
of
$T_{A_2}$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[\bigcap _{v \in V(T_{B_2}) } N^-_{G'}(v, A'_2)]$
such that
$G'[\bigcap _{v \in V(T_{B_2}) } N^-_{G'}(v, A'_2)]$
such that
 \begin{align*} \left |\bigcap _{v \in V(T_{A_2}) } N^-_{G'}(v, A_1) \right | \geq \frac { \alpha ^{2k}}{16}|A_1| \stackrel {({\hbox{6.2}}), ({\hbox{6.1}})}{\ge } 3^k(1-2 \delta )n\, . \end{align*}
\begin{align*} \left |\bigcap _{v \in V(T_{A_2}) } N^-_{G'}(v, A_1) \right | \geq \frac { \alpha ^{2k}}{16}|A_1| \stackrel {({\hbox{6.2}}), ({\hbox{6.1}})}{\ge } 3^k(1-2 \delta )n\, . \end{align*}
Since
![]() $A'_2 \cap B'_2 =\emptyset$
, we have that
$A'_2 \cap B'_2 =\emptyset$
, we have that
![]() $T_{A_2}$
and
$T_{A_2}$
and
![]() $T_{B_2}$
are disjoint.
$T_{B_2}$
are disjoint.
By Lemma 6.4(iii), there is a copy
![]() $T_{B_1}$
of
$T_{B_1}$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[\bigcap _{v \in V(T_{B_2}) } N^+_{G'}(v, B_1) ]$
that is disjoint from both
$G'[\bigcap _{v \in V(T_{B_2}) } N^+_{G'}(v, B_1) ]$
that is disjoint from both
![]() $T_{A_2}$
and
$T_{A_2}$
and
![]() $T_{B_2}$
. Similarly, Lemma 6.4(iii) implies that there is a copy
$T_{B_2}$
. Similarly, Lemma 6.4(iii) implies that there is a copy
![]() $T_{A_1}$
of
$T_{A_1}$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[\bigcap _{v \in V(T_{A_2}) } N^-_{G'}(v, A_1) ]$
that is disjoint from
$G'[\bigcap _{v \in V(T_{A_2}) } N^-_{G'}(v, A_1) ]$
that is disjoint from
![]() $T_{A_2}$
,
$T_{A_2}$
,
![]() $T_{B_1}$
, and
$T_{B_1}$
, and
![]() $T_{B_2}$
. Note that the concatenation of
$T_{B_2}$
. Note that the concatenation of
![]() $T^+, T_{A_1}, T_{A_2}, T_{B_2}, T_{B_1} ,T^-$
yields a
$T^+, T_{A_1}, T_{A_2}, T_{B_2}, T_{B_1} ,T^-$
yields a
![]() $k$
-path from
$k$
-path from
![]() $T^+$
to
$T^+$
to
![]() $T^-$
in
$T^-$
in
![]() $G'$
on
$G'$
on
![]() $6 k$
vertices (with some additional edges), as desired.
$6 k$
vertices (with some additional edges), as desired.
We now outline the proof of the case when
![]() $|A_2 \cap B_2| \ge \tau n$
. By Claim 6.9 with
$|A_2 \cap B_2| \ge \tau n$
. By Claim 6.9 with
![]() $A_1,A_2 \cap B_2,B_1$
playing roles of
$A_1,A_2 \cap B_2,B_1$
playing roles of
![]() $X,Y,Z$
, we obtain a copy
$X,Y,Z$
, we obtain a copy
![]() $T_{A_2 \cap B_2}$
of
$T_{A_2 \cap B_2}$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[A_2 \cap B_2]$
. In fact, we can argue similarly to the previous case to find a copy
$G'[A_2 \cap B_2]$
. In fact, we can argue similarly to the previous case to find a copy
![]() $T_{A_1}$
of
$T_{A_1}$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[A_1]$
and a copy
$G'[A_1]$
and a copy
![]() $T_{B_1}$
of
$T_{B_1}$
of
![]() $\vec {T}_{k}$
in
$\vec {T}_{k}$
in
![]() $G'[B_1]$
so that the concatenation of
$G'[B_1]$
so that the concatenation of
![]() $T^+, T_{A_1}, T_{A_2\cap B_2}, T_{B_1} ,T^-$
yields a
$T^+, T_{A_1}, T_{A_2\cap B_2}, T_{B_1} ,T^-$
yields a
![]() $k$
-path from
$k$
-path from
![]() $T^+$
to
$T^+$
to
![]() $T^-$
in
$T^-$
in
![]() $G'$
on
$G'$
on
![]() $5 k$
vertices, as desired.
$5 k$
vertices, as desired.
6.4 The almost covering lemma
Our goal in this subsection is to prove the following result.
Lemma 6.10.
Let
![]() $k\geq 2$
and let
$k\geq 2$
and let
![]() $Q\geq 10^{1000k}$
. There exists
$Q\geq 10^{1000k}$
. There exists
![]() $n_0\in \mathbb N$
such that if
$n_0\in \mathbb N$
such that if
![]() $G$
is an oriented graph on
$G$
is an oriented graph on
![]() $n\geq n_0$
vertices with
$n\geq n_0$
vertices with
![]() $\delta ^0(G)\geq (\frac {1}{2}-\frac {1}{(20Q)^3})n$
, then
$\delta ^0(G)\geq (\frac {1}{2}-\frac {1}{(20Q)^3})n$
, then
![]() $V(G)$
can be partitioned into sets
$V(G)$
can be partitioned into sets
![]() $S$
of size
$S$
of size
![]() $Q$
or
$Q$
or
![]() $Q+1$
, where for each such
$Q+1$
, where for each such
![]() $S$
we have that
$S$
we have that
![]() $G[S]$
is a tournament,
$G[S]$
is a tournament,
![]() $\delta ^0(G[S]) \geq 2|S|/5$
and
$\delta ^0(G[S]) \geq 2|S|/5$
and
![]() $G[S]$
contains the
$G[S]$
contains the
![]() $k$
th power of a Hamilton cycle. In particular,
$k$
th power of a Hamilton cycle. In particular,
![]() $G$
can be partitioned into at most
$G$
can be partitioned into at most
![]() $n/Q$
vertex-disjoint
$n/Q$
vertex-disjoint
![]() $k$
-cycles.
$k$
-cycles.
Bollobás and Häggkvist [Reference Bollobás and Häggkvist4] proved that for all
![]() ${\varepsilon }\gt 0$
and
${\varepsilon }\gt 0$
and
![]() $k\in \mathbb{N}$
, there exists
$k\in \mathbb{N}$
, there exists
![]() $n_0\in \mathbb{N}$
such that for every tournament
$n_0\in \mathbb{N}$
such that for every tournament
![]() $T$
on
$T$
on
![]() $n\geq n_0$
vertices, if
$n\geq n_0$
vertices, if
![]() $\delta ^0(T)\geq \frac {n}{4}+{\varepsilon } n$
, then
$\delta ^0(T)\geq \frac {n}{4}+{\varepsilon } n$
, then
![]() $C^k_n\subseteq T$
. Draganić, Munhá Correia, and Sudakov [Reference Draganić, Munhá Correia and Sudakov10, Theorem 1.5] gave a refinement of this result, which in particular gives better quantitative bounds. We state their result in a less general form, which is more convenient for our purposes.
$C^k_n\subseteq T$
. Draganić, Munhá Correia, and Sudakov [Reference Draganić, Munhá Correia and Sudakov10, Theorem 1.5] gave a refinement of this result, which in particular gives better quantitative bounds. We state their result in a less general form, which is more convenient for our purposes.
Theorem 6.11.
Let
![]() $k\geq 2$
and let
$k\geq 2$
and let
![]() $n\geq 10^{1000k}$
. If
$n\geq 10^{1000k}$
. If
![]() $T$
is an
$T$
is an
![]() $n$
-vertex tournament with
$n$
-vertex tournament with
![]() $\delta ^0(T)\geq 2n/5$
, then
$\delta ^0(T)\geq 2n/5$
, then
![]() $T$
contains the
$T$
contains the
![]() $k$
th power of a Hamilton cycle.
$k$
th power of a Hamilton cycle.
Therefore, to prove Lemma 6.10, we will first partition
![]() $G$
into vertex-disjoint tournaments each of size
$G$
into vertex-disjoint tournaments each of size
![]() $Q$
or
$Q$
or
![]() $Q+1$
and with minimum semi-degree at least
$Q+1$
and with minimum semi-degree at least
![]() $2(Q+1)/5$
. Then the lemma follows by applying Theorem6.11 to each tournament. We need the following lemma on martingales.
$2(Q+1)/5$
. Then the lemma follows by applying Theorem6.11 to each tournament. We need the following lemma on martingales.
Lemma 6.12 ([Reference Allen, Böttcher, Hàn, Kohayakawa and Person1, Lemma 2.2]). Let
![]() $\Omega$
be a finite probability space and let
$\Omega$
be a finite probability space and let
![]() ${\mathcal{F}}_0, \ldots , {\mathcal{F}}_n$
be partitions of
${\mathcal{F}}_0, \ldots , {\mathcal{F}}_n$
be partitions of
![]() $\Omega$
, with
$\Omega$
, with
![]() ${\mathcal{F}}_{i-1}$
refined by
${\mathcal{F}}_{i-1}$
refined by
![]() ${\mathcal{F}}_i$
for each
${\mathcal{F}}_i$
for each
![]() $i \in [n]$
. For each
$i \in [n]$
. For each
![]() $i\in [n]$
, let
$i\in [n]$
, let
![]() $Y_i$
be a Bernoulli random variable on
$Y_i$
be a Bernoulli random variable on
![]() $\Omega$
that is constant on each part of
$\Omega$
that is constant on each part of
![]() ${\mathcal{F}}_i$
. Furthermore, let
${\mathcal{F}}_i$
. Furthermore, let
![]() $p_i$
be a real-valued random variable on
$p_i$
be a real-valued random variable on
![]() $\Omega$
which is constant on each part of
$\Omega$
which is constant on each part of
![]() ${\mathcal{F}}_{i-1}$
. Let
${\mathcal{F}}_{i-1}$
. Let
![]() $x$
and
$x$
and
![]() $\delta$
be real numbers with
$\delta$
be real numbers with
![]() $\delta \in (0,3/2)$
, and let
$\delta \in (0,3/2)$
, and let
![]() $X \,:\!= Y_1+\ldots +Y_n$
. If
$X \,:\!= Y_1+\ldots +Y_n$
. If
![]() $\sum _{i=1}^n p_i\ge x$
holds almost surely and
$\sum _{i=1}^n p_i\ge x$
holds almost surely and
![]() $\mathbb{E} [Y_i\mid {\mathcal{F}}_{i-1}]\ge p_i$
holds almost surely for all
$\mathbb{E} [Y_i\mid {\mathcal{F}}_{i-1}]\ge p_i$
holds almost surely for all
![]() $i\in [n]$
, then
$i\in [n]$
, then
![]() ${\mathbb{P}}\big (X\lt (1-\delta )x \big )\lt e^{-\delta ^2 x/3}.$
${\mathbb{P}}\big (X\lt (1-\delta )x \big )\lt e^{-\delta ^2 x/3}.$
Proof of Lemma
6.10. Given such a
![]() $Q$
, let
$Q$
, let
![]() $\gamma \,:\!= (20Q)^{-3}$
and let
$\gamma \,:\!= (20Q)^{-3}$
and let
![]() $n_0\in \mathbb N$
be sufficiently large. Let
$n_0\in \mathbb N$
be sufficiently large. Let
![]() $G$
be an oriented graph as in the statement of the lemma. We randomly partition
$G$
be an oriented graph as in the statement of the lemma. We randomly partition
![]() $V(G)$
into
$V(G)$
into
![]() $t\, :\!= \lfloor n/Q\rfloor$
sets
$t\, :\!= \lfloor n/Q\rfloor$
sets
![]() $S_1, S_2, \ldots , S_t$
each of size
$S_1, S_2, \ldots , S_t$
each of size
![]() $Q$
and
$Q$
and
![]() $n-tQ\leq Q-1$
other vertices. Then each
$n-tQ\leq Q-1$
other vertices. Then each
![]() $S_i$
can be viewed as a uniformly random set of
$S_i$
can be viewed as a uniformly random set of
![]() $Q$
vertices from
$Q$
vertices from
![]() $G$
. We claim that with positive probability, all three of the following properties hold:
$G$
. We claim that with positive probability, all three of the following properties hold:
-
(a) at most
 $4 \gamma Q^2 t$
of the
$4 \gamma Q^2 t$
of the
 $G[S_i]$
are not tournaments;
$G[S_i]$
are not tournaments; -
(b) at most
 $ 4 e^{-Q/20^4} t$
of the
$ 4 e^{-Q/20^4} t$
of the
 $G[S_i]$
have minimum semi-degree below
$G[S_i]$
have minimum semi-degree below
 $2(Q+1)/5$
;
$2(Q+1)/5$
; -
(c) for every
 $v\in V(G)$
, there are at least
$v\in V(G)$
, there are at least
 $t/200$
indices
$t/200$
indices
 $i \in [t/100]$
such that
$i \in [t/100]$
such that
 $d^+_G(v, S_i), d^-_G(v, S_i)\ge 2(Q+1)/5$
.
$d^+_G(v, S_i), d^-_G(v, S_i)\ge 2(Q+1)/5$
.
We now show that this implies the lemma. Let
![]() $S_1, \ldots , S_t$
be such that (a)–(c) holds. Let
$S_1, \ldots , S_t$
be such that (a)–(c) holds. Let
![]() $I$
be the set of
$I$
be the set of
![]() $i \in [t]$
such that
$i \in [t]$
such that
![]() $G[S_i]$
is not a tournament or
$G[S_i]$
is not a tournament or
![]() $\delta ^0(G[S_i]) \lt 2(Q+1)/5$
; so
$\delta ^0(G[S_i]) \lt 2(Q+1)/5$
; so
Let
![]() $W \,:\!= V(G) {\setminus} \bigcup _{i \in [t] {\setminus} I} S_i$
, so
$W \,:\!= V(G) {\setminus} \bigcup _{i \in [t] {\setminus} I} S_i$
, so
Recall that every vertex has at most
![]() $2\gamma n$
non-neighbours in
$2\gamma n$
non-neighbours in
![]() $G$
. Together with (c), for each
$G$
. Together with (c), for each
![]() $w \in W$
, the number of
$w \in W$
, the number of
![]() $i \in [t/100] {\setminus} I$
such that
$i \in [t/100] {\setminus} I$
such that
![]() $S_i \subseteq N^+_G(w)\cup N^-_G(w)$
and
$S_i \subseteq N^+_G(w)\cup N^-_G(w)$
and
![]() $d^+_G(w, S_i), d^-_G(w, S_i)\ge 2(Q+1)/5$
is at least
$d^+_G(w, S_i), d^-_G(w, S_i)\ge 2(Q+1)/5$
is at least
Therefore, for each
![]() $w \in W$
, we can greedily assign it a unique
$w \in W$
, we can greedily assign it a unique
![]() $i\in [t/100] {\setminus} I$
such that
$i\in [t/100] {\setminus} I$
such that
![]() $G[S_i\cup \{w\}]$
is a tournament of order
$G[S_i\cup \{w\}]$
is a tournament of order
![]() $Q+1$
with minimum semi-degree at least
$Q+1$
with minimum semi-degree at least
![]() $2(Q+1)/5$
. The lemma holds by applying Theorem6.11 to each tournament.
$2(Q+1)/5$
. The lemma holds by applying Theorem6.11 to each tournament.
To complete the proof, we will show that each of (a)–(c) fails with probability at most
![]() $1/4$
.
$1/4$
.
First, note that
![]() $G$
has at most
$G$
has at most
![]() $(2\gamma n-1)n/2\leq 2 \gamma \binom {n}{2}$
non-edges. For
$(2\gamma n-1)n/2\leq 2 \gamma \binom {n}{2}$
non-edges. For
![]() $i \in [t]$
, let
$i \in [t]$
, let
![]() $X_i$
be the number of non-edges in
$X_i$
be the number of non-edges in
![]() $G[S_i]$
. Then we have
$G[S_i]$
. Then we have
For
![]() $i \in [t]$
, let
$i \in [t]$
, let
![]() $E_i$
be the event that
$E_i$
be the event that
![]() $G[S_i]$
is not a tournament, namely,
$G[S_i]$
is not a tournament, namely,
![]() $G[S_i]$
has some non-edges; let
$G[S_i]$
has some non-edges; let
![]() $X$
be the number of
$X$
be the number of
![]() $i \in [t]$
such that
$i \in [t]$
such that
![]() $G[S_i]$
is not a tournament. Therefore, we obtain
$G[S_i]$
is not a tournament. Therefore, we obtain
By Markov’s inequality, we obtain that
Second, consider
![]() $i \in [t]$
and
$i \in [t]$
and
![]() $v \in S_i$
. Then by Chernoff’s bound for the hypergeometric distribution, we obtain that
$v \in S_i$
. Then by Chernoff’s bound for the hypergeometric distribution, we obtain that
So, by the union bound, for every
![]() $i \in [t]$
, we have
$i \in [t]$
, we have
Let
![]() $Y$
be the number of
$Y$
be the number of
![]() $i\in [t]$
such that
$i\in [t]$
such that
![]() $\delta ^0(G[S_i]) \lt 2(Q+1)/5$
; so
$\delta ^0(G[S_i]) \lt 2(Q+1)/5$
; so
![]() $\mathbb{E} Y\le t e^{-Q/20^4}$
. By Markov’s inequality, we obtain that
$\mathbb{E} Y\le t e^{-Q/20^4}$
. By Markov’s inequality, we obtain that
Finally, fix
![]() $v\in V(G)$
and let
$v\in V(G)$
and let
![]() $t_0 \,:\!= t/100$
. Consider a process of picking a sequence of vertex-disjoint sets
$t_0 \,:\!= t/100$
. Consider a process of picking a sequence of vertex-disjoint sets
![]() $S_1, S_2, \ldots , S_{t_0}$
of size
$S_1, S_2, \ldots , S_{t_0}$
of size
![]() $Q$
, one by one, each time uniformly at random from the remaining vertices. Note that this is equivalent to considering the first
$Q$
, one by one, each time uniformly at random from the remaining vertices. Note that this is equivalent to considering the first
![]() $t_0$
members of our partition
$t_0$
members of our partition
![]() $S_1, \ldots , S_t$
. Now condition on any outcome of
$S_1, \ldots , S_t$
. Now condition on any outcome of
![]() $S_1, \ldots , S_{i-1}$
. Let
$S_1, \ldots , S_{i-1}$
. Let
![]() $S \,:\!= \bigcup _{j\in [i-1]} S_j$
and thus
$S \,:\!= \bigcup _{j\in [i-1]} S_j$
and thus
![]() $|S|= (i-1)Q\lt n/100$
. Then we have
$|S|= (i-1)Q\lt n/100$
. Then we have
![]() $d^+_G(v, V(G){\setminus} S) , \, d^-_G(v, V(G){\setminus} S) \ge (0.49-\gamma )n$
. Therefore, by Chernoff’s bound for the hypergeometric distribution, we obtain that
$d^+_G(v, V(G){\setminus} S) , \, d^-_G(v, V(G){\setminus} S) \ge (0.49-\gamma )n$
. Therefore, by Chernoff’s bound for the hypergeometric distribution, we obtain that
For
![]() $i\in [t_0]$
, let
$i\in [t_0]$
, let
![]() $E_{v, i}$
be the event that
$E_{v, i}$
be the event that
![]() $d^+_G(v, S_i), \, d^-_G(v, S_i)\ge 2(Q+1)/5$
holds. Then we get
$d^+_G(v, S_i), \, d^-_G(v, S_i)\ge 2(Q+1)/5$
holds. Then we get
Let
![]() $Z_v \,:\!= \sum _{i\in [t_0]} \boldsymbol{1}_{E_{v, i}}$
. So by Lemma 6.12 with
$Z_v \,:\!= \sum _{i\in [t_0]} \boldsymbol{1}_{E_{v, i}}$
. So by Lemma 6.12 with
![]() $(n,\mathcal{F}_i,Y_i,p_i,x,\delta ,X) = (t_0, S_i, \boldsymbol{1}_{E_{v, i}}, 2/3, 2t_0/3, 1/4 , Z_v)$
, we obtain that
$(n,\mathcal{F}_i,Y_i,p_i,x,\delta ,X) = (t_0, S_i, \boldsymbol{1}_{E_{v, i}}, 2/3, 2t_0/3, 1/4 , Z_v)$
, we obtain that
By the union bound,
where the last inequality follows as
![]() $t_0 = \lfloor n/Q \rfloor /100$
and
$t_0 = \lfloor n/Q \rfloor /100$
and
![]() $n$
is sufficiently large. This completes the proof of the lemma.
$n$
is sufficiently large. This completes the proof of the lemma.
7. Proofs of Theorems1.4 and 1.5
In this section we combine our auxiliary lemmas to prove both Theorem1.4 and Theorem1.5. In the next subsection, we prove Theorem1.5. The proof of Theorem1.4 is quite standard and follows the same structure as Theorem1.5, so we do not provide all of the calculations in the proof in Section 7.2.
7.1 Proof of Theorem1.5
The second part of Theorem1.5 follows from Proposition 3.3, so we just need to prove the first part. Let
![]() $c \,:\!= 10^{6000}$
and
$c \,:\!= 10^{6000}$
and
![]() $k \ge 2$
. Define constants
$k \ge 2$
. Define constants
![]() $\varepsilon , \eta , d, \zeta , \xi \gt 0$
and
$\varepsilon , \eta , d, \zeta , \xi \gt 0$
and
![]() $n_0, T \in \mathbb N$
so that
$n_0, T \in \mathbb N$
so that
Given any
![]() $n \geq n_0$
, let
$n \geq n_0$
, let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
Let
![]() $\delta \, :\!= \frac {1}{2}-\frac {2}{c^k}$
. Throughout the proof, we simply write good, in-good and out-good to mean
$\delta \, :\!= \frac {1}{2}-\frac {2}{c^k}$
. Throughout the proof, we simply write good, in-good and out-good to mean
![]() $\delta$
-good,
$\delta$
-good,
![]() $\delta$
-in-good and
$\delta$
-in-good and
![]() $\delta$
-out-good (with respect to
$\delta$
-out-good (with respect to
![]() $G$
), respectively.
$G$
), respectively.
Constructing the absorbing path. We first find a good
![]() $k$
-path
$k$
-path
![]() $P_A$
whose first and last
$P_A$
whose first and last
![]() $k$
vertices are denoted by
$k$
vertices are denoted by
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, respectively, and such that
$A_2$
, respectively, and such that
-
(i)
 $|V(P_A)|\leq \eta ^{k} n$
and
$|V(P_A)|\leq \eta ^{k} n$
and -
(ii) for every set
 $L\subseteq V(G){\setminus} V(P_A)$
of size at most
$L\subseteq V(G){\setminus} V(P_A)$
of size at most
 $\eta ^{2k}n$
,
$\eta ^{2k}n$
,
 $G[L \cup V(P_A)]$
contains a spanning
$G[L \cup V(P_A)]$
contains a spanning
 $k$
-path from
$k$
-path from
 $A_1$
to
$A_1$
to
 $A_2$
.
$A_2$
.
To do this, for each
![]() $x\in V(G)$
define
$x\in V(G)$
define
and set
![]() $\mathscr A \,:\!= \bigcup _{x\in V(G)}\mathscr A_x$
.Footnote
5
By Lemma 6.7 (with
$\mathscr A \,:\!= \bigcup _{x\in V(G)}\mathscr A_x$
.Footnote
5
By Lemma 6.7 (with
![]() $3k-1$
playing the role of
$3k-1$
playing the role of
![]() $k$
), we have
$k$
), we have
![]() $|\mathscr A_x|\geq \xi n^{2(3k-1)}$
. Let
$|\mathscr A_x|\geq \xi n^{2(3k-1)}$
. Let
![]() $\mathcal C\subseteq \mathscr A$
be a random collection of
$\mathcal C\subseteq \mathscr A$
be a random collection of
![]() $(3k-1)$
-absorbers in which we independently include each element of
$(3k-1)$
-absorbers in which we independently include each element of
![]() $\mathscr A$
with probability
$\mathscr A$
with probability
![]() $p \,:\!= 4\eta ^{4k/3}n/|\mathscr A|$
. Since
$p \,:\!= 4\eta ^{4k/3}n/|\mathscr A|$
. Since
![]() $\mathbb E(|\mathcal C|) = p|\mathscr A| = 4\eta ^{4k/3}n$
, Markov’s inequality yields that
$\mathbb E(|\mathcal C|) = p|\mathscr A| = 4\eta ^{4k/3}n$
, Markov’s inequality yields that
Moreover, for every
![]() $x\in V(G)$
we have
$x\in V(G)$
we have
Thus, Chernoff’s bound together with the union bound yields that
Finally, let
![]() $X$
be the random variable that counts the number of pairs of
$X$
be the random variable that counts the number of pairs of
![]() $(3k-1)$
-paths
$(3k-1)$
-paths
![]() $P,P'\in \mathcal C$
sharing at least one vertex. Since the number of pairs of
$P,P'\in \mathcal C$
sharing at least one vertex. Since the number of pairs of
![]() $(3k-1)$
-paths on
$(3k-1)$
-paths on
![]() $2(3k-1)$
vertices that intersect in at least one vertex is at most
$2(3k-1)$
vertices that intersect in at least one vertex is at most
![]() $(6k-2)^2n^{12k-5}$
, we have
$(6k-2)^2n^{12k-5}$
, we have
where for the second inequality we used
![]() $|\mathscr A|\geq \xi n^{6k-2}$
. Again by Markov’s inequality, we obtain
$|\mathscr A|\geq \xi n^{6k-2}$
. Again by Markov’s inequality, we obtain
Hence, there is a choice of
![]() $\mathcal C$
for which all three events in (7.1)–(7.3) fail. That is, there is a subset
$\mathcal C$
for which all three events in (7.1)–(7.3) fail. That is, there is a subset
![]() $\mathcal C\subseteq \mathscr A$
such that
$\mathcal C\subseteq \mathscr A$
such that
![]() $|\mathcal C|\leq 8\eta ^{4k/3} n$
,
$|\mathcal C|\leq 8\eta ^{4k/3} n$
,
![]() $X\leq 4\eta ^{2k}n$
, and
$X\leq 4\eta ^{2k}n$
, and
![]() $|\mathcal C\cap \mathscr A_x|\geq 2\eta ^{5k/3} n$
for every
$|\mathcal C\cap \mathscr A_x|\geq 2\eta ^{5k/3} n$
for every
![]() $x\in V(G)$
. Consequently, after deleting at most
$x\in V(G)$
. Consequently, after deleting at most
![]() $X\leq 4\eta ^{2k}n$
elements from
$X\leq 4\eta ^{2k}n$
elements from
![]() $\mathcal C$
, we obtain a set
$\mathcal C$
, we obtain a set
![]() $\mathscr P\subseteq \mathscr A$
of pairwise vertex-disjoint
$\mathscr P\subseteq \mathscr A$
of pairwise vertex-disjoint
![]() $(3k-1)$
-paths such that
$(3k-1)$
-paths such that
We need to connect the
![]() $(3k-1)$
-paths in
$(3k-1)$
-paths in
![]() $\mathscr P$
. To do that, we modify them so that they are all good
$\mathscr P$
. To do that, we modify them so that they are all good
![]() $k$
-paths. This follows from a simple application of Lemma 6.2. More precisely, let
$k$
-paths. This follows from a simple application of Lemma 6.2. More precisely, let
![]() $P\in \mathscr P$
be a fixed
$P\in \mathscr P$
be a fixed
![]() $(3k-1)$
-path and let
$(3k-1)$
-path and let
![]() $T_1$
and
$T_1$
and
![]() $T_2$
be the first and last
$T_2$
be the first and last
![]() $3k-1$
vertices of
$3k-1$
vertices of
![]() $P$
, respectively. As
$P$
, respectively. As
![]() $P$
has
$P$
has
![]() $6k-2$
vertices,
$6k-2$
vertices,
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are disjoint. Further, let
$T_2$
are disjoint. Further, let
![]() $T'_1$
be the first
$T'_1$
be the first
![]() $2k-1$
vertices in
$2k-1$
vertices in
![]() $T_1$
; let
$T_1$
; let
![]() $T''_1$
be the last
$T''_1$
be the last
![]() $k$
vertices in
$k$
vertices in
![]() $T_1$
; let
$T_1$
; let
![]() $T'_2$
be the last
$T'_2$
be the last
![]() $2k-1$
vertices in
$2k-1$
vertices in
![]() $T_2$
; let
$T_2$
; let
![]() $T''_2$
be the first
$T''_2$
be the first
![]() $k$
vertices in
$k$
vertices in
![]() $T_2$
. Since
$T_2$
. Since
![]() $T'_1$
and
$T'_1$
and
![]() $T'_2$
induce transitive tournaments, Lemma 6.2 yields transitive tournaments on
$T'_2$
induce transitive tournaments, Lemma 6.2 yields transitive tournaments on
![]() $k$
vertices
$k$
vertices
![]() $T^*_1\subseteq T'_1$
and
$T^*_1\subseteq T'_1$
and
![]() $T^*_2\subseteq T'_2$
, where
$T^*_2\subseteq T'_2$
, where
![]() $T^*_1$
is in-good and
$T^*_1$
is in-good and
![]() $T^*_2$
is out-good. Suppose
$T^*_2$
is out-good. Suppose
![]() $P$
is a
$P$
is a
![]() $(3k-1)$
-absorber for a vertex
$(3k-1)$
-absorber for a vertex
![]() $x\in V(G)$
, meaning that both
$x\in V(G)$
, meaning that both
![]() $T_1T_2=T'_1T''_1T''_2T'_2$
and
$T_1T_2=T'_1T''_1T''_2T'_2$
and
![]() $T_1xT_2$
form
$T_1xT_2$
form
![]() $(3k-1)$
-paths. It is easy to see that both
$(3k-1)$
-paths. It is easy to see that both
![]() $T^*_1T''_1T''_2 T^*_2$
and
$T^*_1T''_1T''_2 T^*_2$
and
![]() $T^*_1T''_1xT''_2 T^*_2$
induce
$T^*_1T''_1xT''_2 T^*_2$
induce
![]() $k$
-paths in
$k$
-paths in
![]() $G$
(with some additional edges), and hence
$G$
(with some additional edges), and hence
![]() $P' \,:\!= T^*_1T''_1T''_2 T^*_2$
is a stretched
$P' \,:\!= T^*_1T''_1T''_2 T^*_2$
is a stretched
![]() $k$
-absorber for
$k$
-absorber for
![]() $x$
. In other words, after deleting
$x$
. In other words, after deleting
![]() $2k-2$
vertices from
$2k-2$
vertices from
![]() $P$
we obtain a good
$P$
we obtain a good
![]() $k$
-path
$k$
-path
![]() $P'$
such that for every
$P'$
such that for every
![]() $x\in V(G)$
, if
$x\in V(G)$
, if
![]() $P$
is a
$P$
is a
![]() $(3k-1)$
-absorber for
$(3k-1)$
-absorber for
![]() $x$
, then
$x$
, then
![]() $P'$
is a stretched
$P'$
is a stretched
![]() $k$
-absorber for
$k$
-absorber for
![]() $x$
.
$x$
.
Repeat this argument for every
![]() $P\in \mathscr P$
to obtain a new collection
$P\in \mathscr P$
to obtain a new collection
![]() $\mathscr P'$
of vertex-disjoint good
$\mathscr P'$
of vertex-disjoint good
![]() $k$
-paths and observe that due to (7.4), it holds that
$k$
-paths and observe that due to (7.4), it holds that
![]() $|\mathscr P'|\leq 8\eta ^{4k/3}n$
and for every
$|\mathscr P'|\leq 8\eta ^{4k/3}n$
and for every
![]() $x\in V(G)$
there are at least
$x\in V(G)$
there are at least
![]() $\eta ^{5k/3}n$
stretched
$\eta ^{5k/3}n$
stretched
![]() $k$
-absorbers in
$k$
-absorbers in
![]() $\mathscr P'$
.
$\mathscr P'$
.
We connect the paths in
![]() $\mathscr P'$
by greedily applying Lemma 6.8. More precisely, let
$\mathscr P'$
by greedily applying Lemma 6.8. More precisely, let
![]() $\mathscr P' =\!: \{P_1',\ldots , P_r'\}$
where
$\mathscr P' =\!: \{P_1',\ldots , P_r'\}$
where
![]() $r\leq 8\eta ^{4k/3}n$
. Every
$r\leq 8\eta ^{4k/3}n$
. Every
![]() $k$
-path in
$k$
-path in
![]() $\mathscr P'$
starts with an in-good transitive tournament and ends in an out-good transitive tournament, and has size
$\mathscr P'$
starts with an in-good transitive tournament and ends in an out-good transitive tournament, and has size
![]() $4k$
. Suppose that the
$4k$
. Suppose that the
![]() $k$
-paths
$k$
-paths
![]() $P_1',\ldots , P_i'$
are already connected using at most
$P_1',\ldots , P_i'$
are already connected using at most
![]() $4k$
additional vertices for each connection. Then, the number of vertices used in those connections and in the
$4k$
additional vertices for each connection. Then, the number of vertices used in those connections and in the
![]() $k$
-paths in
$k$
-paths in
![]() $\mathscr P'$
is at most
$\mathscr P'$
is at most
![]() $(4k+4k)|\mathscr P'| \leq 8k \cdot 8\eta ^{4k/3} n \leq \zeta n$
. Hence, Lemma 6.8 yields a
$(4k+4k)|\mathscr P'| \leq 8k \cdot 8\eta ^{4k/3} n \leq \zeta n$
. Hence, Lemma 6.8 yields a
![]() $k$
-path connecting
$k$
-path connecting
![]() $P_i'$
with
$P_i'$
with
![]() $P_{i+1}'$
using at most
$P_{i+1}'$
using at most
![]() $4k$
additional vertices and avoiding all vertices from previous connections and all vertices from
$4k$
additional vertices and avoiding all vertices from previous connections and all vertices from
![]() $\mathscr P'$
. Let
$\mathscr P'$
. Let
![]() $P_A$
be the resulting good
$P_A$
be the resulting good
![]() $k$
-path and observe that
$k$
-path and observe that
Hence (i) follows.
Finally, to see (ii), let
![]() $L\subseteq V(G){\setminus} V(P_A)$
be a set of at most
$L\subseteq V(G){\setminus} V(P_A)$
be a set of at most
![]() $\eta ^{2k} n$
vertices. For every
$\eta ^{2k} n$
vertices. For every
![]() $x\in L$
, there are
$x\in L$
, there are
![]() $\eta ^{5k/3} n \gt \eta ^{2k} n$
vertex-disjoint stretched
$\eta ^{5k/3} n \gt \eta ^{2k} n$
vertex-disjoint stretched
![]() $k$
-absorbers for
$k$
-absorbers for
![]() $x$
in
$x$
in
![]() $\mathscr P'$
(so they are subpaths of
$\mathscr P'$
(so they are subpaths of
![]() $P_A$
). Therefore, we may greedily choose a distinct stretched
$P_A$
). Therefore, we may greedily choose a distinct stretched
![]() $k$
-absorber for each vertex
$k$
-absorber for each vertex
![]() $x\in L$
, and use their absorbing properties to ensure we can indeed find the desired
$x\in L$
, and use their absorbing properties to ensure we can indeed find the desired
![]() $k$
-path as in (ii).
$k$
-path as in (ii).
Choosing a reservoir. Choose a set
![]() $S\subseteq V(G){\setminus} V(P_A)$
of size
$S\subseteq V(G){\setminus} V(P_A)$
of size
![]() $\eta ^{3k}n$
uniformly at random. As
$\eta ^{3k}n$
uniformly at random. As
![]() $\delta ^0(G) \ge \delta n + |V(P_A)|$
, for every vertex
$\delta ^0(G) \ge \delta n + |V(P_A)|$
, for every vertex
![]() $v\in V(G)$
, we have
$v\in V(G)$
, we have
![]() $\mathbb E(|N^+_G(v, S)|), \mathbb E(|N^-_G(v, S)|) \geq \delta |S|$
. Similarly, for every out-good transitive tournament
$\mathbb E(|N^+_G(v, S)|), \mathbb E(|N^-_G(v, S)|) \geq \delta |S|$
. Similarly, for every out-good transitive tournament
![]() $T^+$
in
$T^+$
in
![]() $G$
, we have
$G$
, we have
 \begin{equation*} \mathbb E\left (\left |\bigcap _{x\in V(T^+)} N^+_G(x, S)\right |\right ) \ge \eta ^{3k} \left |\bigcap _{x\in V(T^+)} N^+_G(x) {\setminus} V(P_A) \right |\, \ge \left (\frac {(2k-1)\delta - k + 1}{k2^{2k - 1}} - \eta ^k \right )|S| .\end{equation*}
\begin{equation*} \mathbb E\left (\left |\bigcap _{x\in V(T^+)} N^+_G(x, S)\right |\right ) \ge \eta ^{3k} \left |\bigcap _{x\in V(T^+)} N^+_G(x) {\setminus} V(P_A) \right |\, \ge \left (\frac {(2k-1)\delta - k + 1}{k2^{2k - 1}} - \eta ^k \right )|S| .\end{equation*}
We say that an out-good transitive tournament
![]() $T^+\subseteq V(G){\setminus} S$
is out-bad for
$T^+\subseteq V(G){\setminus} S$
is out-bad for
![]() $S$
if
$S$
if
 \begin{equation*}\left |\bigcap _{x\in V(T^+)} N^+_G(x, S)\right | \lt \frac {(2k-1)(\delta - \zeta ^k)-k+1}{k2^{2k-1}} (|S|+k)\,;\end{equation*}
\begin{equation*}\left |\bigcap _{x\in V(T^+)} N^+_G(x, S)\right | \lt \frac {(2k-1)(\delta - \zeta ^k)-k+1}{k2^{2k-1}} (|S|+k)\,;\end{equation*}
that is,
![]() $T^{+}$
is not
$T^{+}$
is not
![]() $(\delta -\zeta ^k)$
-out-good in
$(\delta -\zeta ^k)$
-out-good in
![]() $G[S\cup V(T^+)]$
. We define in-bad for
$G[S\cup V(T^+)]$
. We define in-bad for
![]() $S$
analogously. Thus, using Chernoff’s bound for the hypergeometric distribution together with the union bound, we obtain
$S$
analogously. Thus, using Chernoff’s bound for the hypergeometric distribution together with the union bound, we obtain
 \begin{align*} &\mathbb P\left (\delta ^0(G[S]) \leq \left (\delta - \frac {\zeta ^k}{2}\right )|S|\right ) \lt 1/2,\\ &\mathbb P\left (\text{$\exists $ an out-good transitive tournament $T^{+}$ that is out-bad for $S$}\right ) \lt 1/4 \text{ and } \\ &\mathbb P\left (\text{$\exists $ an in-good transitive tournament $T^{-}$ that is in-bad for $S$}\right ) \lt 1/4. \end{align*}
\begin{align*} &\mathbb P\left (\delta ^0(G[S]) \leq \left (\delta - \frac {\zeta ^k}{2}\right )|S|\right ) \lt 1/2,\\ &\mathbb P\left (\text{$\exists $ an out-good transitive tournament $T^{+}$ that is out-bad for $S$}\right ) \lt 1/4 \text{ and } \\ &\mathbb P\left (\text{$\exists $ an in-good transitive tournament $T^{-}$ that is in-bad for $S$}\right ) \lt 1/4. \end{align*}
Hence, there is a set
![]() $\mathfrak R\subseteq V(G){\setminus} V(P_A)$
such that
$\mathfrak R\subseteq V(G){\setminus} V(P_A)$
such that
-
(a)
 $|\mathfrak R| = \eta ^{3k} n$
and
$|\mathfrak R| = \eta ^{3k} n$
and -
(b) for any vertex-disjoint out-good transitive tournament
 $T^+$
and in-good transitive tournament
$T^+$
and in-good transitive tournament
 $T^-$
, both on
$T^-$
, both on
 $k$
vertices in
$k$
vertices in
 $V(G){\setminus} (V(P_A)\cup \mathfrak R)$
, we haveand moreover in
$V(G){\setminus} (V(P_A)\cup \mathfrak R)$
, we haveand moreover in \begin{equation*}\delta ^0(G[\mathfrak R\cup V(T^+)\cup V(T^-)] \geq \Big (\delta -\zeta ^k\Big )|\mathfrak R|,\end{equation*}
\begin{equation*}\delta ^0(G[\mathfrak R\cup V(T^+)\cup V(T^-)] \geq \Big (\delta -\zeta ^k\Big )|\mathfrak R|,\end{equation*}
 $G[\mathfrak R\cup V(T^+)\cup V(T^-)]$
the tournaments
$G[\mathfrak R\cup V(T^+)\cup V(T^-)]$
the tournaments
 $T^{+}$
and
$T^{+}$
and
 $T^-$
are
$T^-$
are
 $(\delta -\zeta ^k)$
-out-good and
$(\delta -\zeta ^k)$
-out-good and
 $(\delta -\zeta ^k)$
-in-good, respectively.
$(\delta -\zeta ^k)$
-in-good, respectively.
Covering most vertices and final absorption. Our goal for this part is to find a
![]() $k$
-cycle that contains
$k$
-cycle that contains
![]() $P_A$
as a subpath and covers all but at most
$P_A$
as a subpath and covers all but at most
![]() $\eta ^{2k} n$
vertices from
$\eta ^{2k} n$
vertices from
![]() $V(G)$
. After that, we apply (ii) to finish the proof.
$V(G)$
. After that, we apply (ii) to finish the proof.
Let
![]() $G' \,:\!= G{\setminus} (V(P_A)\cup \mathfrak R)$
and
$G' \,:\!= G{\setminus} (V(P_A)\cup \mathfrak R)$
and
![]() $Q \,:\!= 10^{1000(2k-1)}$
. Apply Lemma 4.1 with parameters
$Q \,:\!= 10^{1000(2k-1)}$
. Apply Lemma 4.1 with parameters
![]() $\varepsilon , d$
and
$\varepsilon , d$
and
![]() $t_0 \,:\!= 1/\varepsilon ^2$
, to obtain a partition
$t_0 \,:\!= 1/\varepsilon ^2$
, to obtain a partition
![]() $\{V_0, V_1, \ldots , V_t\}$
of
$\{V_0, V_1, \ldots , V_t\}$
of
![]() $V(G')$
where
$V(G')$
where
![]() $1/\varepsilon ^2 \leq t \leq T$
. Thus, Lemma 4.3 yields a spanning oriented subgraph
$1/\varepsilon ^2 \leq t \leq T$
. Thus, Lemma 4.3 yields a spanning oriented subgraph
![]() $R_o$
of the reduced digraph of
$R_o$
of the reduced digraph of
![]() $G'$
, with
$G'$
, with
 \begin{align*} \delta ^0(R_o) &\geq \left ( \frac {\delta ^0(G')}n - 2 d \right ) t \geq \left ( \frac {\delta ^0(G) - |V(P_A)\cup \mathfrak R|} n - 2 d \right ) t\\ & \stackrel {{(i),\ (a)}}{\geq } \ \left ( \frac {1}{2}-\frac {1}{c^k}-\eta ^{3k} -\eta ^{k} - 2 d \right ) t \geq \left (\frac {1}{2}-\frac {2}{c^k}\right )t \ge \left (\frac {1}{2}-\frac {1}{(20Q)^3}\right )t . \end{align*}
\begin{align*} \delta ^0(R_o) &\geq \left ( \frac {\delta ^0(G')}n - 2 d \right ) t \geq \left ( \frac {\delta ^0(G) - |V(P_A)\cup \mathfrak R|} n - 2 d \right ) t\\ & \stackrel {{(i),\ (a)}}{\geq } \ \left ( \frac {1}{2}-\frac {1}{c^k}-\eta ^{3k} -\eta ^{k} - 2 d \right ) t \geq \left (\frac {1}{2}-\frac {2}{c^k}\right )t \ge \left (\frac {1}{2}-\frac {1}{(20Q)^3}\right )t . \end{align*}
Apply Lemma 6.10 with
![]() $R_o,2k-1$
playing the roles of
$R_o,2k-1$
playing the roles of
![]() $G,k$
to obtain a partition of
$G,k$
to obtain a partition of
![]() $V(R_o)$
into
$V(R_o)$
into
![]() $(2k-1)$
-cycles
$(2k-1)$
-cycles
![]() $C_1,\ldots , C_r$
each of them of size
$C_1,\ldots , C_r$
each of them of size
![]() $Q$
or
$Q$
or
![]() $Q+1$
and
$Q+1$
and
By our choice of
![]() $\varepsilon$
, for every
$\varepsilon$
, for every
![]() $i\in [r]$
, we can apply Lemma 4.8 to
$i\in [r]$
, we can apply Lemma 4.8 to
![]() $C_i$
with
$C_i$
with
![]() $\eta ^{2k}/2$
playing the role of
$\eta ^{2k}/2$
playing the role of
![]() $\eta$
. Thus, we obtain
$\eta$
. Thus, we obtain
![]() $(2k-1)$
-paths
$(2k-1)$
-paths
![]() $P_1, \ldots , P_r$
covering all vertices of
$P_1, \ldots , P_r$
covering all vertices of
![]() $G'$
except at most
$G'$
except at most
 \begin{align} |V(G') {\setminus} \bigcup _{i \in [r]} V(P_i) | \le \varepsilon n + \frac {\eta ^{2k}}{2}\cdot \frac {n}{t}\cdot {t} \leq \frac {2\eta ^{2k}n}{3}\, \end{align}
\begin{align} |V(G') {\setminus} \bigcup _{i \in [r]} V(P_i) | \le \varepsilon n + \frac {\eta ^{2k}}{2}\cdot \frac {n}{t}\cdot {t} \leq \frac {2\eta ^{2k}n}{3}\, \end{align}
vertices.
Roughly speaking, we shall connect these
![]() $(2k-1)$
-paths and the absorbing
$(2k-1)$
-paths and the absorbing
![]() $k$
-path
$k$
-path
![]() $P_A$
into a
$P_A$
into a
![]() $k$
-cycle by applying Lemma 6.2 and property (b) of
$k$
-cycle by applying Lemma 6.2 and property (b) of
![]() $\mathfrak R$
together with Lemma 6.8. In fact, we first modify these
$\mathfrak R$
together with Lemma 6.8. In fact, we first modify these
![]() $(2k-1)$
-paths
$(2k-1)$
-paths
![]() $P_1, \ldots , P_r$
to get good
$P_1, \ldots , P_r$
to get good
![]() $k$
-paths. For a fixed
$k$
-paths. For a fixed
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $T_1$
and
$T_1$
and
![]() $T_2$
be the first and last
$T_2$
be the first and last
![]() $(2k-1)$
vertices of
$(2k-1)$
vertices of
![]() $P_i$
, respectively. Due to Lemma 6.2, there are
$P_i$
, respectively. Due to Lemma 6.2, there are
![]() $k$
-vertex in-good and out-good transitive tournaments
$k$
-vertex in-good and out-good transitive tournaments
![]() $T_1'\subseteq T_1$
and
$T_1'\subseteq T_1$
and
![]() $T_2'\subseteq T_2$
, respectively. It is easy to see that if we delete from
$T_2'\subseteq T_2$
, respectively. It is easy to see that if we delete from
![]() $P_i$
the vertices in
$P_i$
the vertices in
![]() $T_1{\setminus} T_1'$
and
$T_1{\setminus} T_1'$
and
![]() $T_2{\setminus} T_2'$
then we obtain a
$T_2{\setminus} T_2'$
then we obtain a
![]() $k$
-path from
$k$
-path from
![]() $T_1'$
to
$T_1'$
to
![]() $T_2'$
. Applying the same argument for every
$T_2'$
. Applying the same argument for every
![]() $i\in [r]$
we obtain a collection of good
$i\in [r]$
we obtain a collection of good
![]() $k$
-paths
$k$
-paths
![]() $\{P_1',\ldots , P_r'\}$
covering almost all vertices from
$\{P_1',\ldots , P_r'\}$
covering almost all vertices from
![]() $G'$
. In particular, if
$G'$
. In particular, if
![]() $L \,:\!= V(G'){\setminus} \big (\bigcup _{i\in [r]} V(P_i')\big )$
then, using (7.5) we have
$L \,:\!= V(G'){\setminus} \big (\bigcup _{i\in [r]} V(P_i')\big )$
then, using (7.5) we have
 \begin{align} |L|\leq |V(G') {\setminus} \bigcup _{i \in [r]} V(P_i) | + 2(k-1)r \leq \frac {3\eta ^{2k} n}{4} . \end{align}
\begin{align} |L|\leq |V(G') {\setminus} \bigcup _{i \in [r]} V(P_i) | + 2(k-1)r \leq \frac {3\eta ^{2k} n}{4} . \end{align}
Set
![]() $P_{r+1}' \,:\!= P_A$
. From now on, operations over the indices are assumed to be modulo
$P_{r+1}' \,:\!= P_A$
. From now on, operations over the indices are assumed to be modulo
![]() $r+1$
. We now connect the
$r+1$
. We now connect the
![]() $k$
-paths
$k$
-paths
![]() $\mathcal P' \,:\!= \{P_1',\ldots , P_r', P_{r+1}'\}$
into the
$\mathcal P' \,:\!= \{P_1',\ldots , P_r', P_{r+1}'\}$
into the
![]() $k$
-cycle using only vertices from
$k$
-cycle using only vertices from
![]() $\mathfrak R$
. Let
$\mathfrak R$
. Let
![]() $T_{j}^{+}$
and
$T_{j}^{+}$
and
![]() $T^-_j$
be the out-good and in-good tournaments at the end of and the start of
$T^-_j$
be the out-good and in-good tournaments at the end of and the start of
![]() $P_{j}'$
, respectively. Suppose the
$P_{j}'$
, respectively. Suppose the
![]() $k$
-paths
$k$
-paths
![]() $P_1',\ldots , P_{i-1}'$
are already connected into a single
$P_1',\ldots , P_{i-1}'$
are already connected into a single
![]() $k$
-path
$k$
-path
![]() $P_{i-1}^*$
using at most
$P_{i-1}^*$
using at most
![]() $6k(i-1)$
additional vertices, all from
$6k(i-1)$
additional vertices, all from
![]() $\mathfrak R$
. Furthermore,
$\mathfrak R$
. Furthermore,
![]() $P^*_{i-1}$
is obtained by connecting
$P^*_{i-1}$
is obtained by connecting
![]() $T_{j-1}^{+}$
to
$T_{j-1}^{+}$
to
![]() $T_{j}^-$
for
$T_{j}^-$
for
![]() $j \in [i-1]$
. Due to (b) and the fact that
$j \in [i-1]$
. Due to (b) and the fact that
we may apply Lemma 6.8 to the oriented graph
![]() $G[\mathfrak R\cup V(T_{i-1}^+)\cup V(T_i^-)]$
. More precisely, we have
$G[\mathfrak R\cup V(T_{i-1}^+)\cup V(T_i^-)]$
. More precisely, we have
and moreover in
![]() $G[\mathfrak R\cup V(T_{i-1}^+)\cup V(T_i^-)]$
the tournaments
$G[\mathfrak R\cup V(T_{i-1}^+)\cup V(T_i^-)]$
the tournaments
![]() $T_{i-1}^{+}$
and
$T_{i-1}^{+}$
and
![]() $T_i^-$
are
$T_i^-$
are
![]() $(\delta -\zeta ^k)$
-out-good and
$(\delta -\zeta ^k)$
-out-good and
![]() $(\delta -\zeta ^k)$
-in-good, respectively. Thus, since the number of vertices from
$(\delta -\zeta ^k)$
-in-good, respectively. Thus, since the number of vertices from
![]() $\mathfrak R \cup V(T_{i-1}^+)\cup V(T_i^-)$
used in connecting so far is at most
$\mathfrak R \cup V(T_{i-1}^+)\cup V(T_i^-)$
used in connecting so far is at most
![]() $6k(i-1)\leq 6k(r+1)\leq 7kt/Q \leq \zeta |\mathfrak R|$
, Lemma 6.8 yields a
$6k(i-1)\leq 6k(r+1)\leq 7kt/Q \leq \zeta |\mathfrak R|$
, Lemma 6.8 yields a
![]() $k$
-path on at most
$k$
-path on at most
![]() $6k$
vertices completely contained in
$6k$
vertices completely contained in
![]() $\mathfrak R \cup V(T_{i-1}^+)\cup V(T_i^-)$
, from
$\mathfrak R \cup V(T_{i-1}^+)\cup V(T_i^-)$
, from
![]() $T_{i-1}^+$
to
$T_{i-1}^+$
to
![]() $T^-_i$
and avoiding all previous connecting
$T^-_i$
and avoiding all previous connecting
![]() $k$
-paths. We obtain
$k$
-paths. We obtain
![]() $P^*_i$
as desired.
$P^*_i$
as desired.
Therefore, we can greedily connect all consecutive
![]() $k$
-paths
$k$
-paths
![]() $P_1',\ldots , P_{r+1}'$
using vertex-disjoint
$P_1',\ldots , P_{r+1}'$
using vertex-disjoint
![]() $k$
-paths completely contained in
$k$
-paths completely contained in
![]() $\mathfrak R$
(including connecting from
$\mathfrak R$
(including connecting from
![]() $P_{r+1}'$
to
$P_{r+1}'$
to
![]() $P_1'$
). Let
$P_1'$
). Let
![]() $H'$
be the
$H'$
be the
![]() $k$
-cycle obtained in this way. Note that
$k$
-cycle obtained in this way. Note that
![]() $H'$
covers all vertices from
$H'$
covers all vertices from
![]() $V(G){\setminus} L$
except possibly some vertices in
$V(G){\setminus} L$
except possibly some vertices in
![]() $\mathfrak R$
. Thus,
$\mathfrak R$
. Thus,
Finally, using (ii), we absorb all vertices in
![]() $V(G){\setminus} V(H')$
into
$V(G){\setminus} V(H')$
into
![]() $P_A$
(which is a subpath of
$P_A$
(which is a subpath of
![]() $H'$
) and obtain a
$H'$
) and obtain a
![]() $k$
th power of a Hamilton cycle in
$k$
th power of a Hamilton cycle in
![]() $G$
.
$G$
.
7.2 Proof of Theorem1.4
Define additional constants
![]() $\gamma , \xi \gt 0$
and
$\gamma , \xi \gt 0$
and
![]() $n_0,T \in \mathbb N$
such that
$n_0,T \in \mathbb N$
such that
Given any
![]() $n \geq n_0$
, let
$n \geq n_0$
, let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex digraph as in the statement of the theorem.
$n$
-vertex digraph as in the statement of the theorem.
Constructing the absorbing path. First, we find an absorbing
![]() $2$
-path
$2$
-path
![]() $P_A$
in
$P_A$
in
![]() $G$
that starts with an edge
$G$
that starts with an edge
![]() $a_1a_2$
and ends with an edge
$a_1a_2$
and ends with an edge
![]() $a_3a_4$
so that
$a_3a_4$
so that
-
(i)
 $|V(P_A)|\leq 32\gamma n$
and
$|V(P_A)|\leq 32\gamma n$
and -
(ii) for every set
 $L\subseteq V(G){\setminus} V(P_A)$
of size at most
$L\subseteq V(G){\setminus} V(P_A)$
of size at most
 $\gamma ^{2}n$
,
$\gamma ^{2}n$
,
 $G[L\cup V(P_A)]$
contains a spanning
$G[L\cup V(P_A)]$
contains a spanning
 $2$
-path from
$2$
-path from
 $a_1a_2$
to
$a_1a_2$
to
 $a_3a_4$
.
$a_3a_4$
.
To construct
![]() $P_A$
, we proceed as in the proof of Theorem1.5 above. More precisely, given
$P_A$
, we proceed as in the proof of Theorem1.5 above. More precisely, given
![]() $v\in V(G)$
define
$v\in V(G)$
define
![]() $\mathscr A_v \,:\!= \{P \colon P \text{ is an absorber for $v$}\}$
and
$\mathscr A_v \,:\!= \{P \colon P \text{ is an absorber for $v$}\}$
and
![]() $\mathscr A \,:\!= \bigcup _{v\in V(G)}\mathscr A_v$
. In particular, recalling Definition 5.4, note that the sets in
$\mathscr A \,:\!= \bigcup _{v\in V(G)}\mathscr A_v$
. In particular, recalling Definition 5.4, note that the sets in
![]() $\mathscr A$
each have size
$\mathscr A$
each have size
![]() $8$
. Note that Lemma 5.5 with
$8$
. Note that Lemma 5.5 with
![]() $k=2$
, implies that
$k=2$
, implies that
![]() $|\mathscr A_v|\geq \xi n^8$
for every
$|\mathscr A_v|\geq \xi n^8$
for every
![]() $v\in V(G)$
. Similarly to before, take a random subset
$v\in V(G)$
. Similarly to before, take a random subset
![]() $\mathscr B\subseteq \mathscr A$
, in which every element is taken with probability
$\mathscr B\subseteq \mathscr A$
, in which every element is taken with probability
![]() $p \,:\!= \gamma n/|\mathscr A|$
; note that standard concentration inequalities imply that
$p \,:\!= \gamma n/|\mathscr A|$
; note that standard concentration inequalities imply that
Moreover, if
![]() $X$
is the random variable counting the number of pairs
$X$
is the random variable counting the number of pairs
![]() $P,P'\in \mathscr B$
sharing at least one vertex, it is not hard to check that
$P,P'\in \mathscr B$
sharing at least one vertex, it is not hard to check that
![]() $\mathbb P(X\geq \gamma ^{3/2} n)\lt \frac {1}{4}$
. Hence, we may pick a collection
$\mathbb P(X\geq \gamma ^{3/2} n)\lt \frac {1}{4}$
. Hence, we may pick a collection
![]() $\mathscr B\subseteq \mathscr A$
for which all bad events above fail. In particular, after deleting at most
$\mathscr B\subseteq \mathscr A$
for which all bad events above fail. In particular, after deleting at most
![]() $\gamma ^{3/2} n$
elements from such a collection, we obtain a collection
$\gamma ^{3/2} n$
elements from such a collection, we obtain a collection
![]() $\mathscr P\subseteq \mathscr A$
of pairwise vertex-disjoint absorbers satisfying
$\mathscr P\subseteq \mathscr A$
of pairwise vertex-disjoint absorbers satisfying
We can now sequentially connect up the absorbers in
![]() $\mathscr P$
into a single
$\mathscr P$
into a single
![]() $2$
-path
$2$
-path
![]() $P_A$
via repeated applications of Lemma 5.14. In each application of Lemma 5.14, we only introduce at most 16 new vertices; this ensures (i) holds. Further, (7.7) ensures 2 holds.
$P_A$
via repeated applications of Lemma 5.14. In each application of Lemma 5.14, we only introduce at most 16 new vertices; this ensures (i) holds. Further, (7.7) ensures 2 holds.
Choosing a reservoir. We choose a reservoir
![]() $\mathfrak R\subseteq V(G){\setminus} V(P_A)$
, by taking a random set in which every vertex from
$\mathfrak R\subseteq V(G){\setminus} V(P_A)$
, by taking a random set in which every vertex from
![]() $V(G){\setminus} V(P_A)$
is included independently with probability
$V(G){\setminus} V(P_A)$
is included independently with probability
![]() $\gamma ^2/4$
. With positive probability, we have
$\gamma ^2/4$
. With positive probability, we have
-
(a)
 $\gamma ^2n/8 \leq |\mathfrak R|\leq \gamma ^2 n/2$
and
$\gamma ^2n/8 \leq |\mathfrak R|\leq \gamma ^2 n/2$
and -
(b) given any pair of vertex-disjoint edges
 $ab, yz \in E(G)$
, and any set
$ab, yz \in E(G)$
, and any set
 $U \subseteq \mathfrak R {\setminus} \{a,b,y,z\}$
of size at most
$U \subseteq \mathfrak R {\setminus} \{a,b,y,z\}$
of size at most
 $\eta |\mathfrak R|/4$
, there is a
$\eta |\mathfrak R|/4$
, there is a
 $2$
-path
$2$
-path
 $P$
on at most 20 vertices from
$P$
on at most 20 vertices from
 $ab$
to
$ab$
to
 $yz$
in
$yz$
in
 $G[\mathfrak R \cup \{a,b,y,z\}]$
which avoids
$G[\mathfrak R \cup \{a,b,y,z\}]$
which avoids
 $U$
.
$U$
.
Indeed, one can ensure that
![]() $\mathfrak R$
satisfies
$\mathfrak R$
satisfies
![]() $\delta (G[\mathfrak R \cup \{a,b,y,z\}])\geq (8/5+\eta /2)|\mathfrak R \cup \{a,b,y,z\}|$
for all choices of
$\delta (G[\mathfrak R \cup \{a,b,y,z\}])\geq (8/5+\eta /2)|\mathfrak R \cup \{a,b,y,z\}|$
for all choices of
![]() $ab, yz \in E(G)$
; then (b) follows by applying Lemma 5.14.
$ab, yz \in E(G)$
; then (b) follows by applying Lemma 5.14.
Covering most vertices and final absorption. As before, we construct a
![]() $2$
-cycle
$2$
-cycle
![]() $H'$
in
$H'$
in
![]() $G$
covering all vertices except at most
$G$
covering all vertices except at most
![]() $\eta ^2n$
. Let
$\eta ^2n$
. Let
![]() $G' \,:\!= G{\setminus} (V(P_A)\cup \mathfrak R)$
and note that
$G' \,:\!= G{\setminus} (V(P_A)\cup \mathfrak R)$
and note that
Lemma 5.2 with
![]() $k=2$
, and
$k=2$
, and
![]() $\gamma ^3$
playing the role of
$\gamma ^3$
playing the role of
![]() $\eta$
, implies the existence of at most
$\eta$
, implies the existence of at most
![]() $T$
vertex-disjoint
$T$
vertex-disjoint
![]() $2$
-paths in
$2$
-paths in
![]() $G'$
, covering all but at most
$G'$
, covering all but at most
![]() $\gamma ^3 n$
vertices in
$\gamma ^3 n$
vertices in
![]() $G'$
. We can now greedily connect these
$G'$
. We can now greedily connect these
![]() $2$
-paths and the absorbing
$2$
-paths and the absorbing
![]() $2$
-path
$2$
-path
![]() $P_A$
via
$P_A$
via
![]() $\mathfrak R$
by iteratively applying property (b). Let
$\mathfrak R$
by iteratively applying property (b). Let
![]() $H'$
be the resulting
$H'$
be the resulting
![]() $2$
-cycle.
$2$
-cycle.
We finish by noting that
![]() $|V(G){\setminus} V(H')|\leq \gamma ^3 n + |\mathfrak R| \leq \gamma ^2 n$
. Thus, the absorbing property (ii) implies that
$|V(G){\setminus} V(H')|\leq \gamma ^3 n + |\mathfrak R| \leq \gamma ^2 n$
. Thus, the absorbing property (ii) implies that
![]() $H'$
can be extended to the square of a Hamilton cycle in
$H'$
can be extended to the square of a Hamilton cycle in
![]() $G$
.
$G$
.
8. Further discussion and results
8.1 Open problems and approaches to almost covering
In this paper, we asymptotically resolved Conjecture 1.3 in the case of the square of a Hamilton cycle (Theorem1.4). Obtaining a connecting lemma is the main barrier to extending our proof to
![]() $k$
th powers of a Hamilton cycle more generally. For example, consider an
$k$
th powers of a Hamilton cycle more generally. For example, consider an
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with
$G$
with
![]() $\delta (G)= (5/3+o(1))n$
. So certainly
$\delta (G)= (5/3+o(1))n$
. So certainly
![]() $G$
satisfies the minimum total degree condition from the
$G$
satisfies the minimum total degree condition from the
![]() $k=3$
case of Conjecture 1.3. However,
$k=3$
case of Conjecture 1.3. However,
![]() $\delta (G)= (5/3+o(1))n$
only implies that
$\delta (G)= (5/3+o(1))n$
only implies that
![]() $\delta ^+ (G)\geq (2/3+o(1))n$
. Thus, there could be three vertices
$\delta ^+ (G)\geq (2/3+o(1))n$
. Thus, there could be three vertices
![]() $x,y,z\in V(G)$
for which
$x,y,z\in V(G)$
for which
![]() $|N^+_G(x) \cap N^+_G(y) \cap N^+_G(z)|=o(n)$
.
$|N^+_G(x) \cap N^+_G(y) \cap N^+_G(z)|=o(n)$
.
Even worse, if one considers a digraph
![]() $G$
as in the
$G$
as in the
![]() $k \geq 4$
cases of Conjecture 1.3, then there can be
$k \geq 4$
cases of Conjecture 1.3, then there can be
![]() $k$
-sets of vertices in
$k$
-sets of vertices in
![]() $G$
without a single common out-neighbour. In this case, it is impossible to prove a direct analogue of Lemma 5.14 where one can connect any
$G$
without a single common out-neighbour. In this case, it is impossible to prove a direct analogue of Lemma 5.14 where one can connect any
![]() $k$
-set of vertices to another
$k$
-set of vertices to another
![]() $k$
-set via a short
$k$
-set via a short
![]() $k$
-path. Instead, one would likely need a connecting lemma more akin to Lemma 6.8.
$k$
-path. Instead, one would likely need a connecting lemma more akin to Lemma 6.8.
It is also natural to look at minimum degree conditions that force a
![]() $k$
th power of a Hamilton path in a digraph or oriented graph. For example, Ghouila-Houri [Reference Ghouila-Houri21] proved that every
$k$
th power of a Hamilton path in a digraph or oriented graph. For example, Ghouila-Houri [Reference Ghouila-Houri21] proved that every
![]() $n$
-vertex digraph
$n$
-vertex digraph
![]() $G$
with minimum total degree
$G$
with minimum total degree
![]() $\delta (G)\geq n-1$
contains a Hamilton path.Footnote
6
Notice that the extremal construction for Conjecture 1.3 given in Proposition 3.1 actually contains the
$\delta (G)\geq n-1$
contains a Hamilton path.Footnote
6
Notice that the extremal construction for Conjecture 1.3 given in Proposition 3.1 actually contains the
![]() $k$
th power of a Hamilton path. We suspect that the minimum total degree threshold for forcing a
$k$
th power of a Hamilton path. We suspect that the minimum total degree threshold for forcing a
![]() $k$
th power of a Hamilton path in a digraph is lower than the corresponding threshold in Conjecture 1.3. Such a phenomenon may also occur for the minimum semi-degree problem in oriented graphs. Note that the former problem is closely linked to the problem of relaxing the minimum total degree condition in Conjecture 1.3 at the expense of a connectivity-type condition.
$k$
th power of a Hamilton path in a digraph is lower than the corresponding threshold in Conjecture 1.3. Such a phenomenon may also occur for the minimum semi-degree problem in oriented graphs. Note that the former problem is closely linked to the problem of relaxing the minimum total degree condition in Conjecture 1.3 at the expense of a connectivity-type condition.
The almost covering lemma (Lemma 6.10) for Theorem1.5 has a different flavour to analogous results in the literature. Indeed, a standard approach is to follow the strategy that was used in [Reference Komlós, Sárközy and Szemerédi27] to prove Conjecture 1.1 for large graphs. In [Reference Komlós, Sárközy and Szemerédi27], the authors find a
![]() $K_{k+1}$
-tiling in the reduced graph
$K_{k+1}$
-tiling in the reduced graph
![]() $R$
of the host graph
$R$
of the host graph
![]() $G$
so that most vertices in
$G$
so that most vertices in
![]() $R$
are covered by these cliques. Then they use an (undirected) graph analogue of Lemma 4.8 to ‘wind around’ these copies of
$R$
are covered by these cliques. Then they use an (undirected) graph analogue of Lemma 4.8 to ‘wind around’ these copies of
![]() $K_{k+1}$
in
$K_{k+1}$
in
![]() $R$
to obtain a collection of vertex-disjoint
$R$
to obtain a collection of vertex-disjoint
![]() $k$
-paths in
$k$
-paths in
![]() $G$
covering most of the vertices.
$G$
covering most of the vertices.
Thus, a natural approach to Theorem1.5 would have been to first obtain a minimum semi-degree condition that forces an almost spanning
![]() $C^k_{\ell }$
-tiling in an oriented graph
$C^k_{\ell }$
-tiling in an oriented graph
![]() $G$
where
$G$
where
![]() $\ell \geq 2k+1$
. Then one would be able to make use of Lemma 4.8 to obtain an almost covering lemma.
$\ell \geq 2k+1$
. Then one would be able to make use of Lemma 4.8 to obtain an almost covering lemma.
The difficulty with this approach is that it is not immediately clear that one can even obtain such a
![]() $C^k_{\ell }$
-tiling result. For example, a special case of a result of Bollobás and Häggkvist [Reference Bollobás and Häggkvist4, Theorem 4] tells us that there are arbitrarily large regular tournaments (i.e. oriented graphs with the largest possible minimum semi-degree) that do not even contain a single copy of
$C^k_{\ell }$
-tiling result. For example, a special case of a result of Bollobás and Häggkvist [Reference Bollobás and Häggkvist4, Theorem 4] tells us that there are arbitrarily large regular tournaments (i.e. oriented graphs with the largest possible minimum semi-degree) that do not even contain a single copy of
![]() $C^2_{5}$
. This highlights that both Turán-type and
$C^2_{5}$
. This highlights that both Turán-type and
![]() $H$
-tiling problems in oriented graphs are much more subtle than their (undirected) graph analogues. We discuss these problems further in the next subsection.
$H$
-tiling problems in oriented graphs are much more subtle than their (undirected) graph analogues. We discuss these problems further in the next subsection.
8.2 Turán-type and tiling problems for oriented graphs
We say that an oriented graph
![]() $H$
is Turánable if there exists
$H$
is Turánable if there exists
![]() $n_0 \in \mathbb N$
such that for all oriented graphs
$n_0 \in \mathbb N$
such that for all oriented graphs
![]() $G$
on
$G$
on
![]() $n\geq n_0$
vertices, if
$n\geq n_0$
vertices, if
![]() $\delta ^0(G)\geq \lfloor (n-1)/2\rfloor$
, then
$\delta ^0(G)\geq \lfloor (n-1)/2\rfloor$
, then
![]() $H\subseteq G$
. Thus, in the previous subsection, we stated that
$H\subseteq G$
. Thus, in the previous subsection, we stated that
![]() $C^2_{5}$
is not Turánable. If we restrict to odd
$C^2_{5}$
is not Turánable. If we restrict to odd
![]() $n$
, then
$n$
, then
![]() $H$
being Turánable is equivalent to
$H$
being Turánable is equivalent to
![]() $H$
being contained in every sufficiently large regular tournament. This case corresponds to the notion of omnipresent, which was introduced by Bollobás and Häggkvist [Reference Bollobás and Häggkvist4] more than three decades ago.
$H$
being contained in every sufficiently large regular tournament. This case corresponds to the notion of omnipresent, which was introduced by Bollobás and Häggkvist [Reference Bollobás and Häggkvist4] more than three decades ago.
Let
![]() $D_r$
denote the tournament on
$D_r$
denote the tournament on
![]() $3r$
vertices obtained from the
$3r$
vertices obtained from the
![]() $r$
-blow-up
$r$
-blow-up
![]() $C_3(r)$
of the directed cycle
$C_3(r)$
of the directed cycle
![]() $C_3$
by replacing the three independent sets in
$C_3$
by replacing the three independent sets in
![]() $C_3(r)$
with transitive tournaments. The next theorem is a slight generalisation of one of Bollobás and Häggkvist’s results, rephrased into our language.Footnote
7
$C_3(r)$
with transitive tournaments. The next theorem is a slight generalisation of one of Bollobás and Häggkvist’s results, rephrased into our language.Footnote
7
Theorem 8.1 (Bollobás and Häggkvist [Reference Bollobás and Häggkvist4]). A tournament
![]() $T$
is Turánable if and only if
$T$
is Turánable if and only if
![]() $T\subseteq D_r$
for some
$T\subseteq D_r$
for some
![]() $r \in \mathbb N$
.
$r \in \mathbb N$
.
Given
![]() $\ell \geq 2k+1$
, it is not hard to see that
$\ell \geq 2k+1$
, it is not hard to see that
![]() $C^k_\ell \subseteq D_r$
for some
$C^k_\ell \subseteq D_r$
for some
![]() $r\in \mathbb N$
if and only if
$r\in \mathbb N$
if and only if
![]() $\ell \geq 3k$
. In the next subsection, we prove that Theorem8.1 also holds for power of cycles.
$\ell \geq 3k$
. In the next subsection, we prove that Theorem8.1 also holds for power of cycles.
Theorem 8.2.
Let
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $\ell \geq 2k+1$
.
$\ell \geq 2k+1$
.
![]() $C^k_\ell$
is Turánable if and only if
$C^k_\ell$
is Turánable if and only if
![]() $C^k_\ell \subseteq D_r$
for some
$C^k_\ell \subseteq D_r$
for some
![]() $r\in \mathbb N$
. Equivalently,
$r\in \mathbb N$
. Equivalently,
![]() $C^k_\ell$
is Turánable if and only if
$C^k_\ell$
is Turánable if and only if
![]() $\ell \geq 3k$
.
$\ell \geq 3k$
.
In fact, we believe Theorem8.1 can be extended to all oriented graphs.
Conjecture 8.3.
An oriented graph
![]() $H$
is Turánable if and only if there is an
$H$
is Turánable if and only if there is an
![]() $r\in {\mathbb{N}}$
with
$r\in {\mathbb{N}}$
with
![]() $H\subseteq D_r$
.
$H\subseteq D_r$
.
It is also natural to look at the analogous problem for
![]() $H$
-factors. We say that an oriented graph
$H$
-factors. We say that an oriented graph
![]() $H$
is tileable if there exists
$H$
is tileable if there exists
![]() $n_0 \in \mathbb N$
such that for all oriented graphs
$n_0 \in \mathbb N$
such that for all oriented graphs
![]() $G$
on
$G$
on
![]() $n\geq n_0$
vertices with
$n\geq n_0$
vertices with
![]() $n$
divisible by
$n$
divisible by
![]() $|H|$
, if
$|H|$
, if
![]() $\delta ^0(G)\geq \lfloor (n-1)/2\rfloor$
, then
$\delta ^0(G)\geq \lfloor (n-1)/2\rfloor$
, then
![]() $G$
contains an
$G$
contains an
![]() $H$
-factor. For example, it is known that all acyclic oriented graphs (including transitive tournaments) are tileable; see [Reference Yuster37, Theorem 1.3]. Directed cycles are also tileable; see [Reference Li and Molla29, Reference Wang, Yan and Zhang36].
$H$
-factor. For example, it is known that all acyclic oriented graphs (including transitive tournaments) are tileable; see [Reference Yuster37, Theorem 1.3]. Directed cycles are also tileable; see [Reference Li and Molla29, Reference Wang, Yan and Zhang36].
The next question is perhaps the most natural starting point in the study of tileability.
Question 8.4.
Let
![]() $H$
be an oriented graph. Is it true that
$H$
be an oriented graph. Is it true that
![]() $H$
is tileable if and only if
$H$
is tileable if and only if
![]() $H$
is Turánable?
$H$
is Turánable?
Once one knows that an oriented graph
![]() $F$
is Turánable, the next step is to determine the minimum semi-degree threshold for forcing a copy of
$F$
is Turánable, the next step is to determine the minimum semi-degree threshold for forcing a copy of
![]() $F$
in an oriented graph. Thus, given
$F$
in an oriented graph. Thus, given
![]() $n\in \mathbb N$
and a Turánable oriented graph
$n\in \mathbb N$
and a Turánable oriented graph
![]() $F$
, define
$F$
, define
Further, set
![]() $\kappa ^0(F) \,:\!= \lim _{n\to \infty } \tfrac {\text{ex}^0(n,F)}{n}\in [0,1/2]$
. The proof that this limit exists can be shown similarly as in [Reference Mubayi and Zhao31, Proposition 1.2]. In Section 8.4, we prove the following result.
$\kappa ^0(F) \,:\!= \lim _{n\to \infty } \tfrac {\text{ex}^0(n,F)}{n}\in [0,1/2]$
. The proof that this limit exists can be shown similarly as in [Reference Mubayi and Zhao31, Proposition 1.2]. In Section 8.4, we prove the following result.
Proposition 8.5.
There exists a constant
![]() $K\gt 1$
such that, for each
$K\gt 1$
such that, for each
![]() $r\in \mathbb N$
,
$r\in \mathbb N$
,
![]() $\kappa ^0(D_r) \lt \tfrac {1}{2}-\tfrac {1}{K^r}$
.
$\kappa ^0(D_r) \lt \tfrac {1}{2}-\tfrac {1}{K^r}$
.
Note that Proposition 8.5 is quite a useful result. Indeed, given any oriented graph
![]() $F$
such that
$F$
such that
![]() $F \subseteq D_r$
, we have that
$F \subseteq D_r$
, we have that
![]() $\kappa ^0(F) \leq \kappa ^0(D_r)$
; so Proposition 8.5 provides an upper bound on
$\kappa ^0(F) \leq \kappa ^0(D_r)$
; so Proposition 8.5 provides an upper bound on
![]() $\kappa ^0(F)$
.
$\kappa ^0(F)$
.
In fact, if Conjecture 8.3 holds, then
![]() $\kappa ^0(F)\lt 1/2$
for every Turánable oriented graph
$\kappa ^0(F)\lt 1/2$
for every Turánable oriented graph
![]() $F$
. Moreover, since
$F$
. Moreover, since
![]() $C^k_\ell \subseteq D_\ell$
for every
$C^k_\ell \subseteq D_\ell$
for every
![]() $\ell \geq 3k$
, we have the following corollary for powers of cycles.
$\ell \geq 3k$
, we have the following corollary for powers of cycles.
Corollary 8.6.
There is a
![]() $K\gt 1$
such that for every
$K\gt 1$
such that for every
![]() $k\in \mathbb N$
and
$k\in \mathbb N$
and
![]() $\ell \geq 3k$
, we have
$\ell \geq 3k$
, we have
![]() $\kappa ^0(C^k_{\ell })\leq \tfrac {1}{2}-\tfrac {1}{K^\ell }$
.
$\kappa ^0(C^k_{\ell })\leq \tfrac {1}{2}-\tfrac {1}{K^\ell }$
.
Note that the problem of determining
![]() $\kappa ^0(C_{3})$
is a special case of the minimum semi-degree version of the Caccetta–Häggkvist conjecture, and it is known that
$\kappa ^0(C_{3})$
is a special case of the minimum semi-degree version of the Caccetta–Häggkvist conjecture, and it is known that
![]() $1/3\leq \kappa ^0(C_{3})\leq 0.343545$
; see [Reference Lichiardopol30].
$1/3\leq \kappa ^0(C_{3})\leq 0.343545$
; see [Reference Lichiardopol30].
For
![]() $k\geq 2$
, the best lower bound construction we found for an oriented graph with high minimum semi-degree not containing a copy of
$k\geq 2$
, the best lower bound construction we found for an oriented graph with high minimum semi-degree not containing a copy of
![]() $C^k _{3k}$
is given by the blow-up of a semi-regular tournament on
$C^k _{3k}$
is given by the blow-up of a semi-regular tournament on
![]() $3k-1$
vertices. It would be interesting to determine if this is indeed the best construction, at least for the first non-trivial case.
$3k-1$
vertices. It would be interesting to determine if this is indeed the best construction, at least for the first non-trivial case.
Question 8.7.
Is it true that
![]() $\kappa ^0(C^2_{6}) = 2/5$
?
$\kappa ^0(C^2_{6}) = 2/5$
?
Remark 8.8. After this paper first appeared online, Araujo and Xiang [3] made progress on the above-mentioned problems. They disproved Conjecture 8.3, and answered Questions 8.4 and 8.7 in the negative. In particular, regarding Question 8.4, they showed that for all
![]() $r\geq 2$
,
$r\geq 2$
,
![]() $D_r$
is not tileable.
$D_r$
is not tileable.
8.3 Proof of Theorem8.2
Define the tournament
![]() $F_r$
iteratively as follows. Let
$F_r$
iteratively as follows. Let
![]() $F_1 \,:\!= C_3$
. For
$F_1 \,:\!= C_3$
. For
![]() $r\geq 2$
, let
$r\geq 2$
, let
![]() $F_r$
be the vertex-disjoint union of three copies of
$F_r$
be the vertex-disjoint union of three copies of
![]() $F_{r-1}$
, namely,
$F_{r-1}$
, namely,
![]() $F^1$
,
$F^1$
,
![]() $F^2$
, and
$F^2$
, and
![]() $F^3$
, and add all edges from
$F^3$
, and add all edges from
![]() $V(F^1)$
to
$V(F^1)$
to
![]() $V(F^2)$
, from
$V(F^2)$
, from
![]() $V(F^2)$
to
$V(F^2)$
to
![]() $V(F^3)$
, and from
$V(F^3)$
, and from
![]() $V(F^3)$
to
$V(F^3)$
to
![]() $V(F^1)$
. Note that
$V(F^1)$
. Note that
![]() $F_r$
is a regular tournament on
$F_r$
is a regular tournament on
![]() $3^r$
vertices.
$3^r$
vertices.
Before proving Theorem8.2, we make one observation regarding the tournaments
![]() $F_r$
.
$F_r$
.
Observation 8.9.
Let
![]() $k\in \mathbb N$
. If
$k\in \mathbb N$
. If
![]() $2k+1\leq \ell \leq 3k-1$
, then
$2k+1\leq \ell \leq 3k-1$
, then
![]() $C_\ell ^k\not \subseteq F_r$
for all
$C_\ell ^k\not \subseteq F_r$
for all
![]() $r\in \mathbb N$
.
$r\in \mathbb N$
.
Proof. Let
![]() $\ell \geq 2k+1$
and
$\ell \geq 2k+1$
and
![]() $r\in \mathbb N$
. Observe that if
$r\in \mathbb N$
. Observe that if
![]() $|F_r|=3^r\lt \ell$
then clearly
$|F_r|=3^r\lt \ell$
then clearly
![]() ${C}_{\ell }^k\not \subseteq F_r$
.
${C}_{\ell }^k\not \subseteq F_r$
.
Let
![]() $C \,:\!= {C}_{\ell }^k$
be a
$C \,:\!= {C}_{\ell }^k$
be a
![]() $k$
-cycle with vertices
$k$
-cycle with vertices
![]() $v_1,\ldots , v_\ell$
and suppose that
$v_1,\ldots , v_\ell$
and suppose that
![]() $C\subseteq F_r$
(and consequently
$C\subseteq F_r$
(and consequently
![]() $3^r\geq \ell$
). We shall prove by induction on
$3^r\geq \ell$
). We shall prove by induction on
![]() $r$
that
$r$
that
![]() $\ell \geq 3k$
.
$\ell \geq 3k$
.
If
![]() $r=1$
, then
$r=1$
, then
![]() $C\subseteq F_1$
implies that
$C\subseteq F_1$
implies that
![]() $C=C_3$
, that is,
$C=C_3$
, that is,
![]() $k=1$
and
$k=1$
and
![]() $\ell =3$
; so indeed
$\ell =3$
; so indeed
![]() $\ell \geq 3k$
. For the inductive step, let
$\ell \geq 3k$
. For the inductive step, let
![]() $V_1$
,
$V_1$
,
![]() $V_2$
, and
$V_2$
, and
![]() $V_3$
be the three vertex classes such that
$V_3$
be the three vertex classes such that
![]() $V_i \,:\!= V(F^i)$
for
$V_i \,:\!= V(F^i)$
for
![]() $i\in [3]$
, where the
$i\in [3]$
, where the
![]() $F^i$
correspond to the three copies of
$F^i$
correspond to the three copies of
![]() $F_{r-1}$
given in the definition of
$F_{r-1}$
given in the definition of
![]() $F_r$
. If
$F_r$
. If
![]() $V(C)\subseteq V_i$
for some
$V(C)\subseteq V_i$
for some
![]() $i\in [3]$
, then
$i\in [3]$
, then
![]() $C\subseteq F_{r-1}$
and we conclude by induction. Thus, we may assume that this is not the case; notice that this actually implies that
$C\subseteq F_{r-1}$
and we conclude by induction. Thus, we may assume that this is not the case; notice that this actually implies that
![]() $C$
intersects each of
$C$
intersects each of
![]() $V_1$
,
$V_1$
,
![]() $V_2$
, and
$V_2$
, and
![]() $V_3$
. Therefore, without loss of generality, suppose
$V_3$
. Therefore, without loss of generality, suppose
![]() $V_1$
is the class with the smallest number of vertices from
$V_1$
is the class with the smallest number of vertices from
![]() $C$
and that
$C$
and that
![]() $v_1\in V_3$
and
$v_1\in V_3$
and
![]() $v_2\in V_1$
. Then, the
$v_2\in V_1$
. Then, the
![]() $k-1$
successors of
$k-1$
successors of
![]() $v_{2}$
in
$v_{2}$
in
![]() $C$
, namely,
$C$
, namely,
![]() $v_{3}, \ldots , v_{k+1}$
, are all contained in
$v_{3}, \ldots , v_{k+1}$
, are all contained in
![]() $V_1$
, since they are all in the out-neighbourhood of both
$V_1$
, since they are all in the out-neighbourhood of both
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{2}$
. In particular,
$v_{2}$
. In particular,
![]() $|V(C)\cap V_1|\geq k$
. Since
$|V(C)\cap V_1|\geq k$
. Since
![]() $V_1$
is the class with the smallest amount of vertices from
$V_1$
is the class with the smallest amount of vertices from
![]() $C$
, then
$C$
, then
![]() $\ell \geq 3k$
.
$\ell \geq 3k$
.
Now Theorem8.2 is an immediate consequence of Observation 8.9 and Theorem8.1.
Proof of Theorem
8.2. If
![]() $\ell \geq 3k$
, then
$\ell \geq 3k$
, then
![]() ${C}_{\ell }^k\subseteq D_\ell$
, and since
${C}_{\ell }^k\subseteq D_\ell$
, and since
![]() $D_\ell$
is Turánable by Theorem8.1, we have that
$D_\ell$
is Turánable by Theorem8.1, we have that
![]() ${C}_{\ell }^k$
is Turánable.
${C}_{\ell }^k$
is Turánable.
If
![]() $2k+1\leq \ell \leq 3k-1$
, then Observation 8.9 implies
$2k+1\leq \ell \leq 3k-1$
, then Observation 8.9 implies
![]() ${C}_\ell ^k\not \subseteq F_r$
for all
${C}_\ell ^k\not \subseteq F_r$
for all
![]() $r\in \mathbb N$
. Since
$r\in \mathbb N$
. Since
![]() $F_r$
is itself a regular tournament on
$F_r$
is itself a regular tournament on
![]() $3^r$
vertices with
$3^r$
vertices with
![]() $\delta ^0(F_r)=\frac {1}{2}(3^r-1)$
,
$\delta ^0(F_r)=\frac {1}{2}(3^r-1)$
,
![]() $C_\ell ^k$
is not Turánable by definition.
$C_\ell ^k$
is not Turánable by definition.
8.4 Proof of Proposition 8.5
The proof of Proposition 8.5 makes use of Lemma 6.10. We will also use the following result, which just follows immediately by combining Lemma 1.3 and Theorem 3.5 from [Reference Fox and Sudakov19].
Theorem 8.10 (Fox and Sudakov [Reference Fox and Sudakov19]). Given any
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $\delta \gt 0$
such that the following holds for all
$\delta \gt 0$
such that the following holds for all
![]() $r \in \mathbb N$
and
$r \in \mathbb N$
and
![]() $n\geq \delta ^{-4r/\delta }$
. If
$n\geq \delta ^{-4r/\delta }$
. If
![]() $T$
is an
$T$
is an
![]() $n$
-vertex tournament with
$n$
-vertex tournament with
![]() $\delta ^0 (T) \geq \varepsilon n$
, then
$\delta ^0 (T) \geq \varepsilon n$
, then
![]() $D_r\subseteq T$
.
$D_r\subseteq T$
.
Now we are ready to prove Proposition 8.5.
Proof of Proposition
8.5. Let
![]() $\delta \gt 0$
be the output of Theorem8.10 on input
$\delta \gt 0$
be the output of Theorem8.10 on input
![]() $\varepsilon \,:\!= 2/5$
. Let
$\varepsilon \,:\!= 2/5$
. Let
![]() $K \,:\!= \max \{ 20^{3}\cdot 10^{6000}, 20 ^3 \cdot \delta ^{-12/\delta } \}$
and
$K \,:\!= \max \{ 20^{3}\cdot 10^{6000}, 20 ^3 \cdot \delta ^{-12/\delta } \}$
and
![]() $Q \,:\!= \max \{10^{2000},\delta ^{-4r/\delta } \}$
; so
$Q \,:\!= \max \{10^{2000},\delta ^{-4r/\delta } \}$
; so
![]() $K^r \ge (20Q)^3$
.
$K^r \ge (20Q)^3$
.
Suppose
![]() $G$
is a sufficiently large
$G$
is a sufficiently large
![]() $n$
-vertex oriented graph with
$n$
-vertex oriented graph with
![]() $\delta ^0 (G) \geq (1/2-1/K^r)n$
. By Lemma 6.10 (with
$\delta ^0 (G) \geq (1/2-1/K^r)n$
. By Lemma 6.10 (with
![]() $k=2$
), certainly there exists a tournament
$k=2$
), certainly there exists a tournament
![]() $T$
on
$T$
on
![]() $Q$
or
$Q$
or
![]() $Q+1$
vertices in
$Q+1$
vertices in
![]() $G$
, such that
$G$
, such that
![]() $\delta ^0 (T) \geq 2|T|/5$
. As
$\delta ^0 (T) \geq 2|T|/5$
. As
![]() $|T|\geq \delta ^{-4r/\delta }$
, Theorem8.10 implies that
$|T|\geq \delta ^{-4r/\delta }$
, Theorem8.10 implies that
![]() $D_r \subseteq T \subseteq G$
, as desired.
$D_r \subseteq T \subseteq G$
, as desired.
Acknowledgements
The authors are grateful to the referee for their careful review.
Financial support
Louis Debiasio: Research supported in part by NSF grant DMS-1954170. Jie Han: Research partially supported by the National Natural Science Foundation of China (12371341). Allan Lo: Research supported by EPSRC grants EP/V002279/1 and EP/V048287/1. Theodore Molla: Research supported in part by NSF grants DMS-1800761 and DMS-2154313. Simón Piga: Research partially supported by EPSRC grant EP/V002279/1. Andrew Treglown: Research supported by EPSRC grants EP/V002279/1 and EP/V048287/1.
Data availability statement
There are no additional data beyond that contained within the main manuscript.