Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Janson, Svante
2008.
The largest component in a subcritical random graph with a power law degree distribution.
The Annals of Applied Probability,
Vol. 18,
Issue. 4,
Lelarge, Marc
2009.
Efficient control of epidemics over random networks.
p.
1.
Draief, M.
Ganesh, A.
and
Massoulié, L.
2009.
Exponential Random Graphs as Models of Overlay Networks.
Journal of Applied Probability,
Vol. 46,
Issue. 1,
p.
199.
Ball, Frank
Sirl, David
and
Trapman, Pieter
2009.
Threshold behaviour and final outcome of an epidemic on a random network with household structure.
Advances in Applied Probability,
Vol. 41,
Issue. 3,
p.
765.
Lelarge, Marc
2009.
Efficient control of epidemics over random networks.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 37,
Issue. 1,
p.
1.
Ball, Frank
Sirl, David
and
Trapman, Pieter
2009.
Threshold behaviour and final outcome of an epidemic on a random network with household structure.
Advances in Applied Probability,
Vol. 41,
Issue. 3,
p.
765.
Janson, Svante
2010.
Asymptotic equivalence and contiguity of some random graphs.
Random Structures & Algorithms,
Vol. 36,
Issue. 1,
p.
26.
Hayes, Thomas P.
and
Sinclair, Alistair
2010.
Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques.
Vol. 6302,
Issue. ,
p.
602.
Grimmett, Geoffrey
and
Janson, Svante
2010.
Random graphs with forbidden vertex degrees.
Random Structures & Algorithms,
Vol. 37,
Issue. 2,
p.
137.
Amini, Hamed
Cont, Rama
and
Minca, Andreea
2010.
Resilience to Contagion in Financial Networks.
SSRN Electronic Journal,
Bhamidi, Shankar
van der Hofstad, Remco
and
Hooghiemstra, Gerard
2010.
First passage percolation on random graphs with finite mean degrees.
The Annals of Applied Probability,
Vol. 20,
Issue. 5,
Hatami, Hamed
and
Molloy, Michael
2012.
The scaling window for a random graph with a given degree sequence.
Random Structures & Algorithms,
Vol. 41,
Issue. 1,
p.
99.
SHANG, YILUN
2012.
DISTRIBUTION DYNAMICS FOR SIS MODEL ON RANDOM NETWORKS.
Journal of Biological Systems,
Vol. 20,
Issue. 02,
p.
213.
Lelarge, Marc
2012.
Diffusion and cascading behavior in random networks.
Games and Economic Behavior,
Vol. 75,
Issue. 2,
p.
752.
Bohman, Tom
and
Picollelli, Michael
2012.
SIR epidemics on random graphs with a fixed degree sequence.
Random Structures & Algorithms,
Vol. 41,
Issue. 2,
p.
179.
Peixoto, Tiago P.
2012.
Entropy of stochastic blockmodel ensembles.
Physical Review E,
Vol. 85,
Issue. 5,
Salez, Justin
2013.
Joint Distribution of Distances in Large Random Regular Networks.
Journal of Applied Probability,
Vol. 50,
Issue. 03,
p.
861.
Pavlov, Yu. L.
and
Stepanov, M. M.
2013.
Limit distributions of the number of loops in a random configuration graph.
Proceedings of the Steklov Institute of Mathematics,
Vol. 282,
Issue. 1,
p.
202.
Salez, Justin
2013.
Joint Distribution of Distances in Large Random Regular Networks.
Journal of Applied Probability,
Vol. 50,
Issue. 3,
p.
861.
Amini, Hamed
Draief, Moez
and
Lelarge, Marc
2013.
Flooding in Weighted Sparse Random Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 27,
Issue. 1,
p.
1.

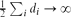 , the probability that the multigraph is simple stays away from 0 if and only if
, the probability that the multigraph is simple stays away from 0 if and only if 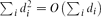 . This was previously known only under extra assumptions on the maximum degree max
. This was previously known only under extra assumptions on the maximum degree max