Ramsey Games Against a One-Armed Bandit
Published online by Cambridge University Press: 03 December 2003
Abstract
We study the following one-person game against a random graph process: the Player's goal is to 2-colour a random sequence of edges 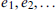 of a complete graph on n vertices, avoiding a monochromatic triangle for as long as possible. The game is over when a monochromatic triangle is created. The online version of the game requires that the Player should colour each edge as it comes, before looking at the next edge.
of a complete graph on n vertices, avoiding a monochromatic triangle for as long as possible. The game is over when a monochromatic triangle is created. The online version of the game requires that the Player should colour each edge as it comes, before looking at the next edge.
While it is not hard to prove that the expected length of this game is about 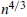 , the proof of the upper bound suggests the following relaxation: instead of colouring online, the random graph is generated in only two rounds, and the Player colours the edges of the first round before the edges of the second round are thrown in. Given the size of the first round, how many edges can there be in the second round for the Player to be likely to win? In the extreme case, when the first round consists of a random graph with
, the proof of the upper bound suggests the following relaxation: instead of colouring online, the random graph is generated in only two rounds, and the Player colours the edges of the first round before the edges of the second round are thrown in. Given the size of the first round, how many edges can there be in the second round for the Player to be likely to win? In the extreme case, when the first round consists of a random graph with 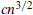 edges, where c is a positive constant, we show that the Player can win with high probability only if constantly many edges are generated in the second round.
edges, where c is a positive constant, we show that the Player can win with high probability only if constantly many edges are generated in the second round.
Information
- Type
- Research Article
- Information
- Combinatorics, Probability and Computing , Volume 12 , Issue 5-6: This issue contains volume twelve, parts five and six , November 2003 , pp. 515 - 545
- Copyright
- Copyright © Cambridge University Press 2003
Footnotes
Partially supported by MCT/CNPq through ProNEx Programme (Proc. CNPq 664107/1997–4) and by CNPq (Proc. 300334/93–1 and 468516/2000–0).
Partially supported by NSF Grant 0071261. The collaboration between the second and third authors is supported by a CNPq/NSF cooperative grant.
Supported by KBN grant 2 PO3A 015 23.
Partially supported by NSF grant DMS-0100298.
- 23
- Cited by

