Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lu, Linyuan
and
Milans, Kevin G.
2015.
Set families with forbidden subposets.
Journal of Combinatorial Theory, Series A,
Vol. 136,
Issue. ,
p.
126.
Patkós, Balázs
2015.
Supersaturation and stability for forbidden subposet problems.
Journal of Combinatorial Theory, Series A,
Vol. 136,
Issue. ,
p.
220.
METHUKU, ABHISHEK
and
PÁLVÖLGYI, DÖMÖTÖR
2017.
Forbidden Hypermatrices Imply General Bounds on Induced Forbidden Subposet Problems.
Combinatorics, Probability and Computing,
Vol. 26,
Issue. 4,
p.
593.
Jiang, Tao
and
Newman, Andrew
2017.
Small Dense Subgraphs of a Graph.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 1,
p.
124.
LOH, PO-SHEN
TAIT, MICHAEL
TIMMONS, CRAIG
and
ZHOU, RODRIGO M.
2018.
Induced Turán Numbers.
Combinatorics, Probability and Computing,
Vol. 27,
Issue. 2,
p.
274.
Méroueh, Arès
2018.
A LYM inequality for induced posets.
Journal of Combinatorial Theory, Series A,
Vol. 155,
Issue. ,
p.
398.
Nagy, Dániel T.
2018.
Forbidden subposet problems with size restrictions.
Journal of Combinatorial Theory, Series A,
Vol. 155,
Issue. ,
p.
42.
Gerbner, Dániel
Methuku, Abhishek
Nagy, Dániel T.
Patkós, Balázs
and
Vizer, Máté
2019.
Forbidding Rank-Preserving Copies of a Poset.
Order,
Vol. 36,
Issue. 3,
p.
611.
Tomon, István
2019.
Forbidden induced subposets of given height.
Journal of Combinatorial Theory, Series A,
Vol. 161,
Issue. ,
p.
537.
Tomon, István
2020.
Packing the Boolean lattice with copies of a poset.
Journal of the London Mathematical Society,
Vol. 101,
Issue. 2,
p.
589.
Sudakov, Benny
Tomon, István
and
Wagner, Adam Zsolt
2022.
Uniform chain decompositions and applications.
Random Structures & Algorithms,
Vol. 60,
Issue. 2,
p.
261.
Axenovich, Maria
and
Winter, Christian
2023.
Poset Ramsey numbers: large Boolean lattice versus a fixed poset.
Combinatorics, Probability and Computing,
p.
1.
Balogh, József
Garcia, Ramon I.
and
Wigal, Michael C.
2025.
On the Number of P-free Set Systems for Tree Posets P.
Order,

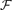 of subsets of [
of subsets of [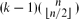 . This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.
. This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.