Hostname: page-component-77f85d65b8-grvzd Total loading time: 0 Render date: 2026-03-30T00:53:23.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Simplifying Inclusion–Exclusion Formulas

Published online by Cambridge University Press:  14 October 2014

XAVIER GOAOC ,
JIŘÍ MATOUŠEK ,
PAVEL PATÁK ,
ZUZANA SAFERNOVÁ  and
MARTIN TANCER
XAVIER GOAOC
Affiliation:
Université Paris–Est Marne-la-Vallée, France (e-mail: goaoc@univ-mlv.fr)
JIŘÍ MATOUŠEK
Affiliation:
Department of Applied Mathematics, Charles University, Malostranské nám. 25, 118 00 Praha 1, Czech Republic (e-mail: matousek@kam.mff.cuni.cz, zuzka@kam.mff.cuni.cz, tancer@kam.mff.cuni.cz) Institute of Theoretical Computer Science, ETH Zurich, 8092 Zurich, Switzerland
PAVEL PATÁK
Affiliation:
Department of Algebra, Charles University, Sokolovská 83, 186 75 Praha 8, Czech Republic (e-mail: patak@kam.mff.cuni.cz)
ZUZANA SAFERNOVÁ
Affiliation:
Department of Applied Mathematics, Charles University, Malostranské nám. 25, 118 00 Praha 1, Czech Republic (e-mail: matousek@kam.mff.cuni.cz, zuzka@kam.mff.cuni.cz, tancer@kam.mff.cuni.cz)
MARTIN TANCER
Affiliation:
Department of Applied Mathematics, Charles University, Malostranské nám. 25, 118 00 Praha 1, Czech Republic (e-mail: matousek@kam.mff.cuni.cz, zuzka@kam.mff.cuni.cz, tancer@kam.mff.cuni.cz)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 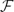$\mathcal{F}$ = {F1, F2,. . ., Fn} be a family of n sets on a ground set S, such as a family of balls in ℝd. For every finite measure μ on S, such that the sets of 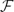$\mathcal{F}$ are measurable, the classical inclusion–exclusion formula asserts that

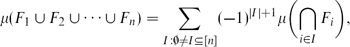$\[\mu(F_1\cup F_2\cup\cdots\cup F_n)=\sum_{I:\emptyset\ne I\subseteq[n]} (-1)^{|I|+1}\mu\biggl(\bigcap_{i\in I} F_i\biggr),\]$
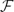that is, the measure of the union is expressed using measures of various intersections. The number of terms in this formula is exponential in n, and a significant amount of research, originating in applied areas, has been devoted to constructing simpler formulas for particular families $\mathcal{F}$. We provide an upper bound valid for an arbitrary 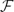$\mathcal{F}$: we show that every system 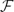$\mathcal{F}$ of n sets with m non-empty fields in the Venn diagram admits an inclusion–exclusion formula with mO(log2n) terms and with ±1 coefficients, and that such a formula can be computed in mO(log2n) expected time. For every ϵ > 0 we also construct systems with Venn diagram of size m for which every valid inclusion–exclusion formula has the sum of absolute values of the coefficients at least Ω(m2−ϵ).

Keywords

Primary 05A19Secondary 05A1505E45

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Issue 2 , March 2015 , pp. 438 - 456
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Attali, D. and Edelsbrunner, H. (2007) Inclusion–exclusion formulas from independent complexes. Discrete Comput. Geom. 37 59–77.CrossRefGoogle Scholar
[2]Björklund, A., Husfeldt, T., Kaski, P. and Koivisto, M. (2008) The travelling salesman problem in bounded degree graphs. In Automata, Languages and Programming I, Vol. 5125 of Lecture Notes in Computer Science, Springer, pp. 198–209.CrossRefGoogle Scholar
[3]Björklund, A., Husfeldt, T. and Koivisto, M. (2009) Set partitioning via inclusion–exclusion. SIAM J. Comput. 39 546–563.CrossRefGoogle Scholar
[4]Bonferroni, C. E. (1936) Teoria statistica delle classi e calcolo delle probabilità. Pubbl. d. R. Ist. Super. di Sci. Econom. e Commerciali di Firenze 8 1–62.Google Scholar
[5]Cohn, H. (2004) Projective geometry over $\mathbb F_1$ and the Gaussian binomial coefficients. Amer. Math. Monthly 111 487–495.Google Scholar
[6]Dohmen, K. (2003) Improved Bonferroni Inequalities via Abstract Tubes, Vol. 1826 of Lecture Notes in Mathematics, Springer.Google Scholar
[7]Edelsbrunner, H. and Ramos, E. A. (1997) Inclusion–exclusion complexes for pseudodisk collections. Discrete Comput. Geom. 17 287–306.CrossRefGoogle Scholar
[8]Galambos, J. (1996) Bonferroni-Type Inequalities with Applications, Springer.Google Scholar
[9]Hatcher, A. (2001) Algebraic Topology, Cambridge University Press.Google Scholar
[10]Hoffmann, M., Okamoto, Y., Ruiz-Vargas, A., Scheder, D. and Solymosi, J. (2012) Solution to GWOP problem 17 ‘A Regional Oracle’. Oral presentation, Tenth Gremo Workshop on Open Problems, Bergün (GR), Switzerland.Google Scholar
[11]Kahn, J., Linial, N. and Samorodnitsky, A. (1996) Inclusion–exclusion: Exact and approximate. Combinatorica 16 465–477.CrossRefGoogle Scholar
[12]Knuth, D. E. (1997) The Art of Computer Programming 2, Addison-Wesley.Google Scholar
[13]Kratky, K. W. (1978) The area of intersection of n equal circular disks. J. Phys. A 11 1017–1024.CrossRefGoogle Scholar
[14]Linial, N. and Nisan, N. (1990) Approximate inclusion–exclusion. Combinatorica 10 349–365.CrossRefGoogle Scholar
[15]Matoušek, J. (2003) Using the Borsuk–Ulam Theorem, Universitext, Springer.Google Scholar
[16]Munkres, J. R. (1984) Elements of Algebraic Topology, Addison-Wesley.Google Scholar
[17]Naiman, D. Q. and Wynn, H. P. (1992) Inclusion–exclusion–Bonferroni identities and inequalities for discrete tube-like problems via Euler characteristics. Ann. Statist. 20 43–76.CrossRefGoogle Scholar
[18]Naiman, D. Q. and Wynn, H. P. (1997) Abstract tubes, improved inclusion–exclusion identities and inequalities and importance sampling. Ann. Statist. 25 1954–1983.CrossRefGoogle Scholar
[19]Nederlof, J. and van Rooij, J. M. M. (2010) Inclusion/exclusion branching for partial dominating set and set splitting. In Parameterized and Exact Computation, Vol. 6478 of Lecture Notes in Computer Science, Springer, pp. 204–215.Google Scholar
[20]Pólya, G. and Alexanderson, G. L. (1971) Gaussian binomial coefficients. Elem. Math. 26 102–109.Google Scholar
[21]Perrot, G., Cheng, B., Gibson, K. D., Vila, J., Palmer, K. A., Nayeem, A., Maigret, B. and Scheraga, H. A. (1992) MSEED: A program for the rapid analytical determination of accessible surface areas and their derivatives. J. Comput. Chem. 13 1–11.CrossRefGoogle Scholar
[22]van Rooij, J. M. M., Nederlof, J. and van Dijk, T. C. (2009) Inclusion/exclusion meets measure and conquer: Exact algorithms for counting dominating sets. In Algorithms: ESA 2009, Vol. 5757 of Lecture Notes in Computer Science, Springer, pp. 554–565.Google Scholar
[23]Stanley, R. P. (1997) Enumerative Combinatorics 1, Vol. 49 of Cambridge Studies in Advanced Mathematics, Cambridge University Press. Corrected reprint of the 1986 original.Google Scholar
[24]Yang, A. Y., Ganesh, A., Zhou, Z., Sastry, S. S. and Ma, Y. (2010) Fast L1-Minimization algorithms for robust face recognition. arXiv:1007.3753Google Scholar