Hostname: page-component-6766d58669-kn6lq Total loading time: 0 Render date: 2026-05-14T16:38:53.047Z Has data issue: false hasContentIssue false
  • English
  • Français

A spanning bandwidth theorem in random graphs

Part of: Graph theory

Published online by Cambridge University Press:  13 December 2021

Peter Allen ,
Julia Böttcher ,
Julia Ehrenmüller ,
Jakob Schnitzer  and
Anusch Taraz
Peter Allen
Affiliation:
London School of Economics, Department of Mathematics, Houghton Street, London WC2A 2AE, UK
Julia Böttcher*
Affiliation:
London School of Economics, Department of Mathematics, Houghton Street, London WC2A 2AE, UK
Julia Ehrenmüller
Affiliation:
Technische Universität Hamburg, Institut fìr Mathematik, Am Schwarzenberg-Campus 3, 21073 Hamburg, Germany
Jakob Schnitzer
Affiliation:
Universität Hamburg, Fachbereich Mathematik, Bundesstrasse 55, 20146 Hamburg Germany
Anusch Taraz
Affiliation:
Technische Universität Hamburg, Institut fìr Mathematik, Am Schwarzenberg-Campus 3, 21073 Hamburg, Germany
*
*Corresponding author. Email: j.boettcher@lse.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The bandwidth theorem of Böttcher, Schacht and Taraz states that any n-vertex graph G with minimum degree 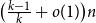$\big(\tfrac{k-1}{k}+o(1)\big)n$ contains all n-vertex k-colourable graphs H with bounded maximum degree and bandwidth o(n). Recently, a subset of the authors proved a random graph analogue of this statement: for 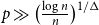$p\gg \big(\tfrac{\log n}{n}\big)^{1/\Delta}$ a.a.s. each spanning subgraph G of G(n,p) with minimum degree 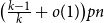$\big(\tfrac{k-1}{k}+o(1)\big)pn$ contains all n-vertex k-colourable graphs H with maximum degree 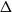$\Delta$, bandwidth o(n), and at least 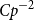$C p^{-2}$ vertices not contained in any triangle. This restriction on vertices in triangles is necessary, but limiting. In this paper, we consider how it can be avoided. A special case of our main result is that, under the same conditions, if additionally all vertex neighbourhoods in G contain many copies of 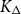$K_\Delta$ then we can drop the restriction on H that 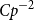$Cp^{-2}$ vertices should not be in triangles.

Keywords

random graphsspanning subgraphssparse regularity

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C35: Extremal problems

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 4 , July 2022 , pp. 598 - 628
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allen, P., Böttcher, J., Ehrenmüller, J. and Taraz, A. (2020) The bandwidth theorem in sparse graphs. Adv. Comb. Paper No. 6, 60.Google Scholar
Allen, P., Böttcher, J., Hàn, H., Kohayakawa, Y. and Person, Y. Blow-up lemmas for sparse graphs. Submitted, arXiv:1612.00622.Google Scholar
Böttcher, J. (2017) Large-scale structures in random graphs. In Surveys in Combinatorics 2017, Vol. 440 of London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge, pp. 87–140.CrossRefGoogle Scholar
Böttcher, J., Schacht, M. and Taraz, A. (2009) Proof of the bandwidth conjecture of BollobÁs and Komlós. Math. Ann. 343(1) 175–205.CrossRefGoogle Scholar
Dirac, G. A. (1952) Some theorems on abstract graphs. Proc. London Math. Soc. (3) 2 69–81.CrossRefGoogle Scholar
Fischer, M., Škorić, N., Steger, A. and Trujić, M. Triangle resilience of the square of a Hamilton cycle in random graphs. Submitted, arXiv:1809.07534.Google Scholar
Gerke, S., Kohayakawa, Y., Rödl, V. and Steger, A. (2007) Small subsets inherit sparse $\varepsilon$ -regularity. J. Comb. Theory Ser. B 97(1) 34–56.CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of P. Erdös. In Combinatorial Theory and its Applications, II (Proc. Colloq., Balatonfüred, 1969), pp. 601–623.Google Scholar
Janson, S., Łuczak, T. and Rucinski, A. (2000) Random Graphs. Wiley-Interscience Series in Discrete Mathematics and Optimization. Wiley-Interscience, New York.CrossRefGoogle Scholar
Kohayakawa, Y. (1997) Szemerédi’s regularity lemma for sparse graphs. In Foundations of Computational Mathematics (Rio de Janeiro, 1997), Springer, Berlin, pp. 216–230.CrossRefGoogle Scholar
Kohayakawa, Y. and Rödl, V. (2003) Szemerédi’s regularity lemma and quasi-randomness. In Recent Advances in Algorithms and Combinatorics, Vol. 11 of CMS Books in Mathematics/Ouvrages Mathematics SMC, Springer, New York, pp. 289–351.CrossRefGoogle Scholar
Komlós, J., Sárközy, G. N. and Szemerédi, E. (1997) Blow-up lemma. Combinatorica 17(1) 109–123.CrossRefGoogle Scholar
Komlós, J., Sárközy, G. N. and Szemerédi, E. (1998) Proof of the Seymour conjecture for large graphs. Ann. Comb. 2(1) 43–60.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2009) Embedding large subgraphs into dense graphs. In Surveys in Combinatorics 2009, Vol. 365 of London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge, pp. 137–167.CrossRefGoogle Scholar
Lee, C. and Sudakov, B. (2012) Dirac’s theorem for random graphs. Random Struct. Algorithms 41(3) 293–305.10.1002/rsa.20419CrossRefGoogle Scholar
Scott, A. (2011) Szemerédi’s regularity lemma for matrices and sparse graphs. Comb. Probab. Comput. 20(3) 455–466.CrossRefGoogle Scholar