Hostname: page-component-89b8bd64d-46n74 Total loading time: 0 Render date: 2026-05-13T09:31:22.536Z Has data issue: false hasContentIssue false
  • English
  • Français

Spanning trees in random regular uniform hypergraphs

Part of: Graph theory

Published online by Cambridge University Press:  26 May 2021

Catherine Greenhill ,
Mikhail Isaev  and
Gary Liang
Catherine Greenhill*
Affiliation:
School of Mathematics and Statistics, UNSW Sydney, Sydney, NSW 2052, Australia
Mikhail Isaev
Affiliation:
School of Mathematical Sciences, Monash University, Clayton, VIC 3800, Australia
Gary Liang
Affiliation:
School of Mathematics and Statistics, UNSW Sydney, Sydney, NSW 2052, Australia
*
*Corresponding author. Email: c.greenhill@unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 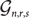$${{\mathcal G}_{n,r,s}}$$ denote a uniformly random r-regular s-uniform hypergraph on the vertex set {1, 2, … , n}. We establish a threshold result for the existence of a spanning tree in 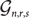$${{\mathcal G}_{n,r,s}}$$, restricting to n satisfying the necessary divisibility conditions. Specifically, we show that when s ≥ 5, there is a positive constant ρ(s) such that for any r ≥ 2, the probability that 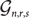$${{\mathcal G}_{n,r,s}}$$ contains a spanning tree tends to 1 if r > ρ(s), and otherwise this probability tends to zero. The threshold value ρ(s) grows exponentially with s. As 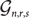$${{\mathcal G}_{n,r,s}}$$ is connected with probability that tends to 1, this implies that when r ≤ ρ(s), most r-regular s-uniform hypergraphs are connected but have no spanning tree. When s = 3, 4 we prove that 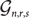$${{\mathcal G}_{n,r,s}}$$ contains a spanning tree with probability that tends to 1, for any r ≥ 2. Our proof also provides the asymptotic distribution of the number of spanning trees in 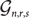$${{\mathcal G}_{n,r,s}}$$ for all fixed integers r, s ≥ 2. Previously, this asymptotic distribution was only known in the trivial case of 2-regular graphs, or for cubic graphs.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C65: Hypergraphs 05C70: Factorization, matching, partitioning, covering and packing

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 29 - 53
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

Supported by the Australian Research Council Discovery Project DP190100977.

‡

Supported by the Australian Research Council Discovery Early Career Researcher Award DE200101045.

References

Aldosari, H. S. and Greenhill, C. (2019) Enumerating sparse uniform hypergraphs with given degree sequence and forbidden edges. Eur. J. Comb. 77 68–77.Google Scholar
Aldosari, H. S. and Greenhill, C. (2021) The average number of spanning hypertrees in sparse uniform hypergraphs. Discrete Math. 344 112192.Google Scholar
Altman, D., Greenhill, C., Isaev, M. and Ramadurai, R. (2020) A threshold result for loose Hamiltonicity in random regular uniform hypergraphs. J. Comb. Theory (Ser. B) 142 307–373.CrossRefGoogle Scholar
Bacher, R. On the enumeration of labelled hypertrees and of labelled bipartite trees. arXiv:1102.2708Google Scholar
Beeri, C., Fagin, R., Maier, D. and Yannakakis, M. (1983) On the desirability of acyclic database schemes. J. ACM (JACM) 30(3) 479–513.CrossRefGoogle Scholar
Bender, E. A. and Canfield, E. R. (1978) The asymptotic number of labeled graphs with given degree sequences. J. Comb. Theory Ser. A 24(3) 296–307.CrossRefGoogle Scholar
Berge, C. (1976) Graphs and Hypergraphs, 2nd edn., North–Holland Publishing Co, New York.Google Scholar
Bollobás, B. (1980) A probabilistic proof of an asymptotic formula for the number of labelled regular graphs. Eur. J. Combinatorics 1(4) 311–316.CrossRefGoogle Scholar
Bollobás, B. (1981) Random graphs. In Combinatorics, Vol. 52 of London Mathematical Society Lecture Note Series (Temperley, H. N. V., ed.), Cambridge University Press, Cambridge, pp. 80–102.CrossRefGoogle Scholar
Boonyasombat, V. (1984) Degree sequences of connected hypergraphs and hypertrees. In Graphs Theory Singapore 1983, Vol. 1073 of Lecture Notes in Mathematics (Koh, K. M. and Yap, H. P., eds), Springer, Berlin, Heidelberg, pp. 236–247.Google Scholar
Brault-Baron, J. (2015) Hypergraph acyclicity revisited. ACM Comput. Surv. 49(3) article 54.Google Scholar
Chu, W. (1986) On an extension of a partition identity and its Abel-analog. J. Math. Res. Exposition 6(4) 37–39.Google Scholar
Cooper, C., Frieze, A., Molloy, M. and Reed, B. (1996) Perfect matchings in random r-regular, s-uniform hypergraphs. Comb. Prob. Comput. 5(1) 1–14.CrossRefGoogle Scholar
Duchet, P. (1995) Hypergraphs. In Handbook of Combinatorics, Vol. 1, MIT Press, Cambridge, Massachusetts, pp. 381–432.Google Scholar
Dumitriu, I. and Zhu, Y. Spectra of random regular hypergraphs. arXiv:1905.06487.Google Scholar
Gorodezky, I. and Pak, I. (2014) Generalized loop-erased random walks and approximate reachability. Random Struct. Algorithms 44(2) 201–223.CrossRefGoogle Scholar
Greenhill, C., Isaev, M. and Liang, G. Spanning trees in random regular uniform hypergraphs. arXiv:2005.07350.Google Scholar
Greenhill, C., Janson, S. and Ruciński, A. (2010) On the number of perfect matchings in random lifts. Comb. Prob. Comput. 19 791–817.CrossRefGoogle Scholar
Greenhill, C., Kwan, M. and Wind, D. (2014) On the number of spanning trees in random regular graphs. Electr. J. Comb. 21(1) 1–45.Google Scholar
Janson, S. (1995) Random regular graphs: asymptotic distributions and contiguity. Comb. Prob. Comput. 4 369–405.CrossRefGoogle Scholar
Kajino, H. (2019) Molecular hypergraph grammar with its application to molecular optimization. In Proceedings of Machine Learning Research, Vol. 97, PMLR, pp. 3183–3191.Google Scholar
Lavault, C. A note on Prüfer-like coding and counting forests of uniform hypertrees. arXiv:1110.0204.Google Scholar
Marsden, J. E. (1974) Elementary Classical Analysis, W.H. Freeman, New York.Google Scholar
McKay, B. D. (1981) Subgraphs of random graphs with specified degrees. Conguressus Numerantium 33 213–223.Google Scholar
Moon, J. W. (1970) Counting Labelled Trees, Vol. 1 of Canadian Mathematical Monographs, Canadian Mathematical Congress, Montreal.Google Scholar
Robinson, R. W. and Wormald, N. C. (1992) Almost all cubic graphs are Hamiltonian. Random Struct. Algorithms 3 117–125.CrossRefGoogle Scholar
Robinson, R. W. and Wormald, N. C. (1994) Almost all regular graphs are Hamiltonian. Random Struct. Algorithms 5 363–374.CrossRefGoogle Scholar
Shannigrahi, S. and Pal, S. P. (2009) Efficient Prüfer-like coding and counting labelled hypertrees. Algorithmica 54(2) 208–225.CrossRefGoogle Scholar
Simon, S. and Wojtczak, D. (2017) Synchronisation games on hypergraphs. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, pp. 402–408.CrossRefGoogle Scholar
Siu, W.-C. (2002) Hypertrees in d-uniform hypergraphs, Ph.D. thesis, Michigan State University. Available from https://search.proquest.com/docview/305546157?pq-origsite=primo.Google Scholar
Sivasubramanian, S. Spanning trees in complete uniform hypergraphs and a connection to extended r-Shi hyperplane arrangements. arXiv:math/0605083.Google Scholar
Warme, D. M. (1998) Spanning Trees in Hypergraphs with Applications to Steiner Trees. Ph.D Thesis, University of Virginia.Google Scholar
Wilf, H. S. (1994) Generatingfunctionology, Academic Press, Cambridge, MA.Google Scholar
Wormald, N. C. (1981) The asymptotic connectivity of labelled regular graphs, J. Comb. Theory Ser. B 31 156–157.CrossRefGoogle Scholar
Wormald, N. C. (1999) Models of random regular graphs. In Surveys in Combinatorics, 1999, Vol. 267 of London Mathematical Society Lecture Note Series (Lamb, J. D. and Preece, D. A., eds), Cambridge University Press, Cambridge, pp. 239–298.Google Scholar