Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-04-30T19:12:07.829Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Construction of Well-Conditioned Hierarchical Bases for 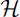(div)-Conforming ℝn Simplicial Elements

Published online by Cambridge University Press:  03 June 2015

Jianguo Xin ,
Wei Cai  and
Nailong Guo
Jianguo Xin
Affiliation:
Department of Mathematics and Statistics, University of North Carolina at Charlotte, Charlotte, NC 28223, USA
Wei Cai*
Affiliation:
Department of Mathematics and Statistics, University of North Carolina at Charlotte, Charlotte, NC 28223, USA
Nailong Guo
Affiliation:
Mathematics and Computer Science Department, Benedict College, Columbia, SC 29204, USA
*
Corresponding author.Email:wcai@uncc.edu
Get access

Abstract

Hierarchical bases of arbitrary order for 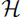(div)-conforming triangular and tetrahedral elements are constructed with the goal of improving the conditioning of the mass and stiffness matrices. For the basis with the triangular element, it is found numerically that the conditioning is acceptable up to the approximation of order four, and is better than a corresponding basis in the dissertation by Sabine Zaglmayr [High Order Finite Element Methods for Electromagnetic Field Computation, Johannes Kepler Universität, Linz, 2006]. The sparsity of the mass matrices from the newly constructed basis and from the one by Zaglmayr is similar for approximations up to order four. The stiffness matrix with the new basis is much sparser than that with the basis by Zaglmayr for approximations up to order four. For the tetrahedral element, it is identified numerically that the conditioning is acceptable only up to the approximation of order three. Compared with the newly constructed basis for the triangular element, the sparsity of the mass matrices from the basis for the tetrahedral element is relatively sparser.

Keywords

65N3065F3565F15Hierarchical basessimplicial (div)-conforming elementsmatrix conditioning
Type
Research Article
Information
Communications in Computational Physics , Volume 14 , Issue 3 , September 2013 , pp. 621 - 638
Copyright
Copyright © Global Science Press Limited 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Brezzi, F. and Fortin, M., Mixed and Hybrid Finite Element Methods, Springer Series in Computational Mathematics, 15. Springer-Verlag, New York, 1991.CrossRefGoogle Scholar
[2]Roberts, J. E. and Thomas, J.-M., Mixed and Hybrid Methods, in Handbook of Numerical Analysis (Edited by Ciarlet, P. G. and Lions, J.-L.), Vol. II, pp. 523–639, North-Holland, Amsterdam, 1991.Google Scholar
[3]Love, A. E. H., A Treatise on the Mathematical Theory of Elasticity, 4th Ed., Dover Publication, New York, 1944.Google Scholar
[4]Stratton, J. A., Electromagnetic Theory, McGraw-Hill, New York, 1941.Google Scholar
[5]Temam, R., Navier-Stokes Equations: Theory and Numerical Analysis. With an appendix by Thomasset, F., 3rd Ed. Studies in Mathematics and Its Applications, 2. North-Holland Publishing, Amsterdam, 1984.Google Scholar
[6]Cowling, T. G., Magnetohydrodynamics, Interscience Tracts on Physics and Astronomy, No. 4. Interscience Publishers, New York, 1957.Google Scholar
[7]Raviart, P. A. and Thomas, J. M., A mixed finite element method for 2nd order elliptic problems, Mathematical aspects of finite element methods (Proc. Conf. Consiglio Naz. delle Ricerche (C.N.R.), Rome, 1975), pp. 292–315. Lecture Notes in Math., Vol. 606, Springer, Berlin, 1977.Google Scholar
[8]Neédélec, J. C., Mixed finite elements in R3, Numer. Math., 35 (1980), pp. 315–341.Google Scholar
[9]Neédélec, J. C., A new family of mixed finite elements in R3, Numer. Math., 50 (1986), pp. 57– 81.Google Scholar
[10]Ciarlet, P. G., Mathematical Elasticity Vol. I. Three-dimensional Elasticity. Studies in Mathematics and Its Applications, 20. North-Holland Publishing, Amsterdam, 1988.Google Scholar
[11]Brezzi, F., Douglas, J. Jr. and Marini, L. D., Two families of mixed finite elements for second order elliptic problems, Numer. Math., 47 (1985), pp. 217–235.Google Scholar
[12]Brezzi, F., Douglas, J. Jr., Duraán, R. and Fortin, M., Mixed finite elements for second order elliptic problems in three variables, Numer. Math., 51 (1987), pp. 237–250.Google Scholar
[13]Hiptmair, R., Canonical construction of finite elements, Math. Comp., 68 (1999), pp. 1325–1346.Google Scholar
[14]Hiptmair, R., Finite elements in computational electromagnetism, Acta Numer., 11 (2002), pp. 227–339.Google Scholar
[15]Arnold, D. N., Falk, R. S. and Winther, R., Finite element exterior calculus, homological techniques, and applications, Acta Numer., 15 (2006), pp. 1–155.Google Scholar
[16]Arnold, D. N., Falk, R. S. and Winther, R., Finite element exterior calculus: from Hodge theory to numerical stability, Bull. Amer. Math. Soc. (N.S.), 47 (2010), pp. 281–354.Google Scholar
[17]Bluck, M. J., Conforming hierarchical basis functions, Commun. Comput. Phys., 12 (2012), pp. 1215–1256.Google Scholar
[18]Ainsworth, M. and Coyle, J., Hierarchic finite element bases on unstructured tetrahedral meshes, Internat. J. Numer. Methods Engrg., 58 (2003), pp. 2103–2130.Google Scholar
[19]Akin, J. E., Finite Elements for Analysis and Design, Academic Press, London, 1994.Google Scholar
[20]Xin, J., Pinchedez, K. and Flaherty, J. E., Implementation of hierarchical bases in FEMLAB for simplicial elements, ACM Trans. Math. Software, 31 (2005), pp. 187–200.Google Scholar
[21]Zaglmayr, S., High Order Finite Element Methods for Electromagnetic Field Computation, Ph.D. Dissertation, Johannes Kepler Universitaät, Linz, 2006.Google Scholar
[22]Babusøka, I., Szabo, B. A. and Katz, I. N., The p-version of the finite element method, SIAM J. Numer. Anal., 18 (1981), pp. 515–545.Google Scholar
[23]Babusøka, I. and Suri, M., The p and h-p versions of the finite element method, basic principles and properties, SIAM Rev., 36 (1994), pp. 578–632.Google Scholar
[24]Carnevali, P., Morris, R. B., Tsuji, Y. and Taylor, G., New basis functions and computational procedures for p-version finite element analysis, Int. J.Num. Meth. Eng., 36 (1993), pp. 3759–3779.Google Scholar
[25]Adjerid, S., Aiffa, M. and Flaherty, J. E., Hierarchical finite element bases for triangular and tetrahedral elements, Comput. Methods Appl. Mech. Engrg., 190 (2001), pp. 2925–2941.Google Scholar
[26]Webb, J. P., Hierarchal vector basis functions of arbitrary order for triangular and tetrahedral finite elements, IEEE Trans. Antennas and Propagation, 47 (1999), pp. 1244–1253.Google Scholar
[27]Ainsworth, M. and Coyle, J., Hierarchic hp-edge element families for Maxwell’s equations on hybrid quadrilateral/triangular meshes, Comput. Methods Appl. Mech. Engrg., 190 (2001), pp. 6709–6733.Google Scholar
[28]Xin, J. and Cai, W., A well-conditioned hierarchical basis for triangular H(curl)-conforming elements, Commun. Comput. Phys., 9 (2011), pp. 780–806.Google Scholar
[29]Xin, J., Guo, N. and Cai, W., On the construction of well-conditioned hierarchical bases for tetrahedral H(curl)-conforming Nédélec element, J. Comput. Math., 29 (2011), pp. 526–542.Google Scholar
[30]Xin, J. and Cai, W., Well-conditioned orthonormal hierarchical L2 bases on Rn simplicial elements, J. Sci. Comput., 50 (2012), pp. 446–461.Google Scholar
[31]Dunkl, C. F. and Xu, Y., Orthogonal Polynomials of Several Variables, Encyclopedia of Mathematics and its Applications, 81. Cambridge University Press, Cambridge, 2001.Google Scholar
[32]Magnus, W., Oberhettinger, F. and Soni, R. P., Formulas and Theorems for the Special Functions of Mathematical Physics, Die Grundlehren der mathematischen Wissenschaften, Band 52, Springer-Verlag, New York, 3rd enlarged edition, 1966.Google Scholar
[33]Dautray, R. and Lions, J.-L., Mathematical Analysis and Numerical Methods for Science and Technology, Vol. 3. Spectral Theory and Applications, Springer-Verlag, Berlin, 1990.Google Scholar
[34]Kellogg, O. D., Foundations of Potential Theory, Reprint from the first edition of 1929. Die Grundlehren der Mathematischen Wissenschaften, Band 31, Springer-Verlag, New York, 1967.Google Scholar
[35]Cockburn, B., Kanschat, G. and Schoötzau, D., A note on discontinuous Galerkin divergence-free solutions for the Navier-Stokes equations, J. Sci. Comput., 31 (2007), pp. 61–73.Google Scholar
[36]Greif, C., Li, D., Schoötzau, D. and Wei, X., A mixed finite element method with exactly divergence-free velocities for incompressible magnetohydrodynamics, Comput. Methods Appl. Mech. Engrg., 199 (2010), pp. 2840–2855.Google Scholar