Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T03:37:40.694Z Has data issue: false hasContentIssue false
  • English
  • Français

A Comparison of Higher-Order Weak Numerical Schemes for Stopped Stochastic Differential Equations

Part of: Probability theory and stochastic processes Stochastic processes Numerical analysis

Published online by Cambridge University Press:  31 August 2016

Francisco Bernal  and
Juan A. Acebrón
Francisco Bernal*
Affiliation:
INESC-ID\IST, TU Lisbon. Rua Alves Redol 9, 1000-029 Lisbon, Portugal Center for Mathematics and its Applications, Department of Mathematics, Instituto Superior Técnico. Av. Rovisco Pais 1049-001 Lisbon, Portugal
Juan A. Acebrón*
Affiliation:
INESC-ID\IST, TU Lisbon. Rua Alves Redol 9, 1000-029 Lisbon, Portugal ISCTE - Instituto Universitário de Lisboa Departamento de Ciências e Tecnologias de Informação. Av. das Forças Armadas 1649-026 Lisbon, Portugal
*
*Corresponding author. Email addresses:francisco.bernal@ist.utl.pt (F. Bernal), juan.acebron@ist.utl.pt (J. A. Acebrón)
*Corresponding author. Email addresses:francisco.bernal@ist.utl.pt (F. Bernal), juan.acebron@ist.utl.pt (J. A. Acebrón)
Get access

Abstract

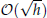We review, implement, and compare numerical integration schemes for spatially bounded diffusions stopped at the boundary which possess a convergence rate of the discretization error with respect to the timestep h higher than . We address specific implementation issues of the most general-purpose of such schemes. They have been coded into a single Matlab program and compared, according to their accuracy and computational cost, on a wide range of problems in up to ℝ48. The paper is self-contained and the code will be made freely downloadable.

Keywords

Weak convergenceFeynman-Kacstochastic differential equationbounded diffusionfirst-exit problem

MSC classification

Secondary: 60G50: Sums of independent random variables; random walks 60-08: Computational methods (not classified at a more specific level) 65-02: Research exposition (monographs, survey articles)
Type
Research Article
Information
Communications in Computational Physics , Volume 20 , Issue 3 , September 2016 , pp. 703 - 732
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Acebrón, J.A., Busico, M.P., Lanucara, P., and Spigler, R., Domain decomposition solution of elliptic boundary-value problems via Monte Carlo and quasi-Monte Carlo methods. SIAM J. Sci. Comp. 27(2), 440–457 (2005).CrossRefGoogle Scholar
[2] Baldi, P., Exact asymptotics for the probability of exit from a domain and applications to simulation. Ann. Probab. 23(4), 1644–1670 (1995).CrossRefGoogle Scholar
[3] Bayer, C., Szepessy, A., and Tempone, R., Adaptive weak approximation of reflected and stopped diffusions. Monte Carlo Methods and Applications 16, 1–67 (2010).CrossRefGoogle Scholar
[4] Bernal, F., Acebrón, J.A., and Anjam, I., A stochastic algorithm based on fast marching for automatic capacitance extraction in non-Manhattan geometries. SIAM J. Imag. Sci. 7(4), 2657–2674 (2014).CrossRefGoogle Scholar
[5] Buchmann, F.M. and Petersen, W.P., An exit probability approach to solving high dimensional Dirichlet problems. SIAM J. Sci. Comput. 28, 1153–1166 (2006).CrossRefGoogle Scholar
[6] Buchmann, F.M., Simulation of stopped diffusions. J. Comput. Phys. 202(2), 446–462 (2005).CrossRefGoogle Scholar
[7] Constantini, C., Pacchiarotti, B., and Sartoretto, F., Numerical approximation for functionals of reflecting diffusion processes. SIAM J. Appl. Math. 58, 73–102 (1998).Google Scholar
[8] Deaconu, M. and Lejay, A., A Random Walk on Rectangles algorithm. Methodol. Comput. Appl. Probab. 8, 135–151 (2006).CrossRefGoogle Scholar
[9] Freidlin, M., Functional Integration and Partial Differential Equations. Princeton University Press (1985).Google Scholar
[10] Giles, M.B., Multi-levelMonte Carlo path simulation. Operations Research, 56(3), 607–617 (2008).CrossRefGoogle Scholar
[11] Giles, M.B. and Bernal, F., Multilevel simulations of expected exit times and other functionals of stopped diffusions. In preparation. (Unpublished)Google Scholar
[12] Giraudo, M.T. and Sacerdote, L., An improved technique for the simulation of first passage times for diffusion processes. Comm. Statist. Simulation Comput. 28(4), 1135–1163 (1999).CrossRefGoogle Scholar
[13] Glasserman, P., Monte Carlo Methods in Financial Engineering. Springer (2003).CrossRefGoogle Scholar
[14] Gobet, E. and Menozzi, S., Stopped diffusion processes: Overshoots and boundary correction. Stoch. Proc. Appl., 120, 130–162, (2010).CrossRefGoogle Scholar
[15] Gobet, E., Euler schemes for the weak approximation of killed diffusion. Stoch. Process. Appl. 87, 167–197 (2000).CrossRefGoogle Scholar
[16] Gobet, E., Euler schemes and half-space approximation for the simulation of diffusions in a domain. ESAIM: Probab. Statist. 5, 261–297 (2001).CrossRefGoogle Scholar
[17] Higham, D.J., Mao, X., Roj, M., Song, Q., and Yin, G.. Mean exit times and the multilevel Monte Carlo method. SIAM J. Uncertainty Quantification, 1(1), 2–18 (2013).CrossRefGoogle Scholar
[18] Iyer, G., Novikov, A., Ryzhik, L., and Zlatos, A., Exit times for diffusions with incompressible drift. SIAM J. Math. Anal. 42, 2484–2498 (2010).CrossRefGoogle Scholar
[19] Jansons, K.M. and Lythe, G.D., Efficient numerical solution of stochastic differential equations using exponential timestepping. J. Statist. Phys. 100(5-6), 1097–1109 (2000).CrossRefGoogle Scholar
[20] Kloeden, P.E. and Platten, E., Numerical Solution of Stochastic Differential Equations. Springer (1999).Google Scholar
[21] Lemaire, P. and Pagés, G., Multilevel Richardson-Romberg extrapolation. To appear in Bernoulli, (2015).CrossRefGoogle Scholar
[22] Mairé, S. and Tanré, E., Some new simulation schemes for the evaluation of Feynman-Kac representations. Monte Carlo Methods and Applications, 14(1), 29–51 (2008).CrossRefGoogle Scholar
[23] Mairé, S. and Simon, M., A partially reflecting random walk on spheres algorithm for electrical impedance tomography. Preprint in arXiv:1502.04318 (2015). (Unpublished)CrossRefGoogle Scholar
[24] Mancini, S., Bernal, F., and Acebrón, J.A., An efficient algorithm for accelerating Monte Carlo approximations of the solution to boundary value problems. J. Sci. Comput. 66(2), 577–597 (2016).CrossRefGoogle Scholar
[25] Mannella, R., Absorbing boundaries and optimal stopping in a stochastic differential equation. Phys. Lett. A 254(5), 257–262 (1999).CrossRefGoogle Scholar
[26] Mascagni, M. and Simonov, N.A., Monte Carlo methods for calculating some physical properties of large molecules, SIAM J. Sci. Comput. 26, 339–357 (2004).CrossRefGoogle Scholar
[27] Michael, J.R., Schucany, W.R., and Haas, R.W., Generating random variates using transformations with multiple roots. Am. Statist. 30, 88–90 (1976).Google Scholar
[28] Milstein, G.N., Weak approximation of a diffusion process in a bounded domain. Stoch. Stoch. Rep. 62, 147–200 (1997).CrossRefGoogle Scholar
[29] Milstein, G.N. and Tretyakov, M.V., Stochastic Numerics for Mathematical Physics. Springer, Berlin (2004).CrossRefGoogle Scholar
[30] Milstein, G.N. and Tretyakov, M.V., The simplest random walks for the Dirichlet problem. Teor. Veroyatnost. I Primenen. 47(1), 39–58 (2002).Google Scholar
[31] Miranda, C., Partial Differential Equations of Elliptic Type. Springer (1970).Google Scholar
[32] Muller, M.E., Some continuous Monte Carlo methods for the Dirichlet problem. Ann. Math. Statist. 27, 569–589 (1956).CrossRefGoogle Scholar
[33] Redner, S., A Guide to First-Passage Processes. Cambridge University Press (2001).CrossRefGoogle Scholar
[34] Schwabedal, J.T.C. and Pikovsky, A., Phase description of stochastic oscillations, Phys. Rev. Lett. 110(20), 204102 (2013).CrossRefGoogle ScholarPubMed
[35] Tamborrino, M., Sacerdote, L., and Jacobsen, M., Weak convergence of marked point processes generated by crossings of multivariate jump processes. Application to neural network modeling. Physica D, 288, 45–52 (2014).CrossRefGoogle Scholar
[36] Talay, D. and Tubaro, L., Expansion of the global error for numerical schemes solving stochastic differential equations. Stoch. Anal. App., 8(4), 94–120 (1990).Google Scholar