Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-24T12:04:51.668Z Has data issue: false hasContentIssue false
  • English
  • Français

On Time-Splitting Pseudospectral Discretization for Nonlinear Klein-Gordon Equation in Nonrelativistic Limit Regime

Published online by Cambridge University Press:  03 June 2015

Xuanchun Dong ,
Zhiguo Xu  and
Xiaofei Zhao
Xuanchun Dong*
Affiliation:
Beijing Computational Science Research Center, Beijing 100084, P.R. China
Zhiguo Xu*
Affiliation:
Beijing Computational Science Research Center, Beijing 100084, P.R. China College of Mathematics, Jilin University, Changchun 130012, P.R. China
Xiaofei Zhao*
Affiliation:
Department of Mathematics, National University of Singapore, Singapore 119076, Singapore
*
Email:dong.xuanchun@gmail.com
Email:xuzg11@csrc.ac.cn
Corresponding author.Email:zhxfnus@gmail.com
Get access

Abstract

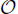In this work, we are concerned with a time-splitting Fourier pseudospectral (TSFP) discretization for the Klein-Gordon (KG) equation, involving a dimensionless parameter ɛ ∊ (0,1]. In the nonrelativistic limit regime, the small ɛ produces high oscillations in exact solutions with wavelength of (ɛ2) in time. The key idea behind the TSFP is to apply a time-splitting integrator to an equivalent first-order system in time, with both the nonlinear and linear subproblems exactly integrable in time and, respectively, Fourier frequency spaces. The method is fully explicit and time reversible. Moreover, we establish rigorously the optimal error bounds of a second-order TSFP for fixed ɛ = 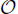(1), thanks to an observation that the scheme coincides with a type of trigonometric integrator. As the second task, numerical studies are carried out, with special efforts made to applying the TSFP in the nonrelativistic limit regime, which are geared towards understanding its temporal resolution capacity and meshing strategy for 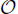(ɛ2)-oscillatory solutions when 0 < ɛ « 1. It suggests that the method has uniform spectral accuracy in space, and an asymptotic 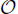(ɛ−2Δt2) temporal discretization error bound (Δt refers to time step). On the other hand, the temporal error bounds for most trigonometric integrators, such as the well-established Gautschi-type integrator in, are 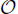(ɛ−4Δt2). Thus, our method offers much better approximations than the Gautschi-type integrator in the highly oscillatory regime. These results, either rigorous or numerical, are valid for a splitting scheme applied to the classical relativistic NLS reformulation as well.

Keywords

35L7065M1265M1565M70Klein-Gordon equationhigh oscillationtime-splittingtrigonometric integratorerror estimatemeshing strategy.
Type
Research Article
Information
Communications in Computational Physics , Volume 16 , Issue 2 , August 2014 , pp. 440 - 466
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ablowitz, M.J., Kruskal, M.D., and Ladik, J.F., Solitary wave collisions, SIAM J. Appl. Math., 36 (1979), pp. 428–437.CrossRefGoogle Scholar
[2]Bainov, D.D. and Minchev, E., Nonexistence of global solutions of the initial-boundary value problem for the nonlinear Klein-Gordon equation, J. Math. Phys. 36 (1995), pp. 756–762.Google Scholar
[3]Bao, W. and Cai, Y., Optimal error estimates of finite difference methods for the Gross- Pitaevskii equation with angular momentum rotation, Math. Comp., 82 (2013), pp. 99–128.Google Scholar
[4]Bao, W. and Cai, Y., Mathematical theory and numerical methods for Bose-Einstein condensation, Kinet. Relat. Mod., 6 (2013), pp. 1–135.Google Scholar
[5]Bao, W. and Dong, X., Numerical methods for computing ground states and dynamics of nonlinear relativistic Hartree equation for boson stars, J. Compt. Phys., 230 (2011), pp. 5449–5469.Google Scholar
[6]Bao, W. and Dong, X., Analysis and comparison of numerical methods for Klein-Gordon equation in nonrelativistic limit regime, Numer. Math., 120 (2012), pp. 189–229.Google Scholar
[7]Bao, W., Jin, S., and Markowich, P.A., Time-splitting spectral approximations for the Schrodinger equation in the semiclassical regime, J. Compt. Phys., 175 (2002), pp. 487–524.Google Scholar
[8]Bao, W., Jin, S., and Markowich, P.A., Numerical studies of time-splitting spectral discretizations of nonlinear Schrodinger equations in the semiclassical regime, SIAM J. Sci. Compt., 25 (2003), pp. 27–64.Google Scholar
[9]Bao, W. and Shen, J., A fourth-order time-splitting Laguerre-Hermite pseudo-spectral method for Bose-Einstein condensates, SIAM J. Sci. Comput., 26 (2005), pp. 2010–2028.Google Scholar
[10]Brenner, P. and Von Wahl, W., Global classical solutions of non-Linear wave equations, Math. Z., 176 (1981), pp. 87–121.Google Scholar
[11]Germund, D. and Ake, B., Numerical Methods in Scientific Computing: Vol. 1, SIAM, 2008.Google Scholar
[12]Cao, W. and Guo, B., Fourier collocation method for solving nonlinear Klein-Gordon equation, J. Comput. Phys. 108 (1993), pp. 296–305.Google Scholar
[13]Davydov, A.S., Quantum Mechanics, 2nd Edition, Pergamon, Oxford, 1976.Google Scholar
[14]Deeba, E.Y. and Khuri, S.A., A decomposition method for solving the nonlinear Klein-Gordon equation, J. Comput. Phys., 124 (1996), pp. 442–448.Google Scholar
[15]Duncan, D.B., Symplectic finite difference approximations of the nonlinear Klein-Gordon equation, SIAM J. Numer. Anal. 34 (1997), pp. 1742–1760.Google Scholar
[16]Deuflhard, P., A study of extrapolation methods based on multistep schemes without parasitic solutions, ZAMP., 30 (1979), pp. 177–189.Google Scholar
[17]Grimm, V., A note on the Gautschi-type method for oscillatory second-order differential equations, Numer. Math., 102 (2005), pp. 61–66.Google Scholar
[18]Grimm, V., On error bounds for the Gautschi-type exponential integrator applied to oscillatory second-order differential equations, Numer. Math., 100 (2005), pp. 71–89.Google Scholar
[19]Hardin, R.H. and Tappert, F.D., Applications of the split-step Fourier method to the numerical solution of nonlinear and variable coefficient wave equations, SIAM Rev. 15 (1973), pp. 423.Google Scholar
[20]Hochbruck, M. and Lubich, Ch., A Gautschi-type method for oscillatory second-order differential equations, Numer. Math., 83 (1999), pp. 402–426.Google Scholar
[21]Hairer, E., Lubich, Ch. and Wanner, G., Geometric Numerical Integration, Springer-Verlag, 2002.Google Scholar
[22]Jimenez, S. and Vazquez, L., Analysis of four numerical schemes for a nonlinear Klein- Gordon equation, Appl. Math. Comput. 35 (1990), pp. 61–94.Google Scholar
[23]Ibrahim, S., Majdoub, M. and Masmoudi, N., Global solutions for a semilinear, twodimensional Klein-Gordon equation with exponential-type nonlinearity, Comm. Pure Appl. Math. 59, (2006), pp. 1639–1658.Google Scholar
[24]Kosecki, R., The unit condition and global existence for a class of nonlinear Klein-Gordon equations, J. Diff. Eqn. 100 (1992), pp. 257–268.Google Scholar
[25]Li, S. and Vu-Quoc, L., Finite difference calculus invariant structure of a class of algorithms for the nonlinear Klein-Gordon equation, SIAM J. Numer. Anal., 32 (1995), pp. 1839–1875.Google Scholar
[26]Machihara, S., The nonrelativistic limit of the nonlinear Klein-Gordon equation, Funkcial. Ekvac., 44 (2), pp. 243–252.Google Scholar
[27]Machihara, S., Nakanishi, K. and Ozawa, T., Nonrelativistic limit in the energy space for nonlinear Klein-Gordon equations, Math. Ann., 322 (2002), pp. 603–621.Google Scholar
[28]Masmoudi, N. and Nakanishi, K., From nonlinear Klein-Gordon equation to a system of coupled nonliner Schrödinger equations, Math. Ann., 324 (2002), pp. 359–389.Google Scholar
[29]Morawetz, C. and Strauss, W., Decay and scattering of solutions of a nonlinear relativistic wave equation, Comm. Pure Appl. Math., 25 (1972), pp. 1–31.Google Scholar
[30]Najman, B., The nonrelativistic limit of the nonlinear Klein-Gordon equation, Nonlinear Anal. 15 (1990), pp. 217–228.Google Scholar
[31]Najman, B., The nonrelativistic limit of Klein-Gordon and Dirac equations, Differential equations with applications in biology, physics, and engineering (Leibnitz, 1989), pp. 291–299, Lecture Notes in Pure and Appl. Math., 133, Dekker, New York, 1991.Google Scholar
[32]Pascual, P.J., Jimenez, S. and Vazquez, L., Numerical simulations of a nonlinear Klein-Gordon model, Applications. Computational physics (Granada, 1994), pp. 211–270, Lecture Notes in Phys., 448, Springer, Berlin, 1995.Google Scholar
[33]Pecher, H., Nonlinear Small Data Scaterring for the Wave and Klein-Gordon Equation, Math. Z., 185 (1984), pp. 261–270.Google Scholar
[34]Sakurai, J.J., Advanced Quantum Mechanics, Addison Wesley, New York, 1967.Google Scholar
[35]Segal, I.E., The Global Cauchy Problem for a Relativistic Scalar Field with Power Interaction, Bull. Soc. Math. Fr., 91 (1963), pp. 129–135.Google Scholar
[36]Shatah, J., Normal forms and quadratic nonlinear Klein-Gordon equations, Commun. Pure Appl. Math. 38 (1985), pp. 685–696.Google Scholar
[37]Shen, J. and Tang, T., Spectral and High-Order Methods with Applications, Science Press, Beijing, 2006.Google Scholar
[38]Simon, J.C.H. and Taflin, E., The cauchy problem for non-linear Klein-Gordon equations, Commun. Math. Phys., 152 (1993), pp. 433–478.CrossRefGoogle Scholar
[39]Strang, G., On the construction and comparison of difference schemes, SIAM J. Numer. Anal., 5 (1968), pp. 506–517.CrossRefGoogle Scholar
[40]Strauss, W., Decay and Asymptotics for □ u = f (u), J. Funct. Anal., 2 (1968), pp. 409–457.Google Scholar
[41]Strauss, W. and Vazquez, L., Numerical solution of a nonlinear Klein-Gordon equation, J. Comput. Phys., 28 (1978), pp. 271–278.Google Scholar
[42]Tourigny, Y., Product approximation for nonlinear Klein-Gordon equations, IMA J. Numer. Anal., 9 (1990), pp. 449–462.Google Scholar
[43]Tsutsumi, M., Nonrelativistic approximation of nonlinear Klein-Gordon equations in two space dimensions, Nonlinear Anal. 8 (1984), pp. 637–643.Google Scholar
[44]Weideman, J.A.C. and Herbst, B.M., Split-step methods for the solution of the nonlinear Schrodinger equation, SIAM J. Numer. Anal., 23 (1986), pp. 485–507.Google Scholar
[45]Yoshida, H., Construction of higher order symplectic integrators, Phys. Lett. A, 150 (1990), pp. 262–268.Google Scholar