1. Introduction
The computational cost of reacting flows’ Computational lFluid Dynamics (CFD) simulations is highly correlated with the number of chemical species included in the kinetic mechanism. In fact, as observed in Cuoci et al. (Reference Cuoci, Frassoldati, Faravelli and Ranzi2013), in the context of operator-splitting methods for inhomogeneous reacting flows (Ren and Pope, Reference Ren and Pope2008), the CPU time associated with both the transport substep and the reaction substep increases nonlinearly with the level of chemical detail. The reaction step, in particular, represents the most time-consuming part of the computation, requiring sometimes even more than 90% of the total computational time (Cuoci et al., Reference Cuoci, Frassoldati, Faravelli and Ranzi2013). Many strategies involving an a priori skeletal reduction have been developed and efficiently coupled with numerical simulations (Nagy and Turányi, Reference Nagy and Turányi2009; Niemeyer, Reference Niemeyer2009; Ranzi et al., Reference Ranzi, Frassoldati, Stagni, Pelucchi, Cuoci and Faravelli2014; Stagni et al., Reference Stagni, Frassoldati, Cuoci, Faravelli and Ranzi2016; Chen et al., Reference Chen, Mehl, Xie and Chen2017), but it is not always possible to opt out of using a high number of species. In many cases, in fact, the use of detailed kinetic mechanisms is still crucial for accurate predictions of slow chemistry, as well as for an accurate description of the pollutants formation.
One effective strategy to alleviate the costs implied with the inclusion of detailed chemical mechanisms in CFD simulations is to consider an adaptive-chemistry approach, as it allows to reduce the CPU time by means of the adaptation of the kinetic mechanism according to the local flame conditions. Several adaptive approaches have been proposed in the literature, such as the Dynamic Adaptive Chemistry and the Pre-Partitioning Adaptive Chemistry (Schwer et al., Reference Schwer, Lu and Green2003; Liang et al., Reference Liang, Stevens and Farrell2009; Shi et al., Reference Shi, Liang, Ge and Reitz2010; Contino et al., Reference Contino, Jeanmart, Lucchini and D’Errico2011; Ren et al., Reference Ren, Liu, Lu, Lu, Oluwole and Goldin2014a, Reference Ren, Xu, Lu and Singer2014b; Komninos, Reference Komninos2015; Liang et al., Reference Liang, Pope and Pepiot2015; Zhou and Wei, Reference Zhou and Wei2016; Newale et al., Reference Newale, Liang, Pope and Pepiot2019, Reference Newale, Pope and Pepiot2020), as well as the use of lookup tables with B-spline interpolants (Bode et al., Reference Bode, Collier, Bisetti and Pitsch2019), with benefits in terms of both CPU time (if compared to the detailed simulations) and accuracy (if compared with simulations using globally reduced mechanisms).
In D’Alessio et al. (Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b, Reference D’Alessio, Parente, Stagni and Cuoci2020c), the authors proposed and validated, for both steady and unsteady laminar methane flames, a data-driven adaptive-chemistry approach called Sample Partitioning Adaptive Reduced Chemistry (SPARC), specifically conceived for operator-splitting numerical solvers, showing its potential in terms of chemical reduction, computational speed-up, and accuracy. The latter is based on two main steps: a preprocessing phase, in which the creation of a library of reduced kinetic mechanisms is accomplished, and a second step, in which the multidimensional adaptive CFD simulation is carried out. The preprocessing phase consists of the three following substeps: the creation of a training dataset, the data partitioning, and the generation of the reduced mechanisms. The offline data partitioning is carried out via local principal component analysis (LPCA; Kambhatla and Leen, Reference Kambhatla and Leen1997; D’Alessio et al., Reference D’Alessio, Attili, Cuoci, Pitsch and Parente2020a), or by means of any other clustering algorithm (D’Alessio et al., Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b). After that, for each group of similar points (cluster), a reduced kinetic mechanism is generated via Directed Relation Graph with Error Propagation (DRGEP; Pepiot-Desjardins and Pitsch, Reference Pepiot-Desjardins and Pitsch2008). The chemical reduction step can also be accomplished using different kinetic reduction techniques such as Computational Singular Perturbation or Intrinsic Low-Dimensional Manifolds (Maas, Reference Maas1998; Valorani et al., Reference Valorani, Creta, Goussis, Lee and Najm2006, Reference Valorani, Creta, Donato, Najm and Goussis2007; König and Maas, Reference König and Maas2009). After this step, a library of reduced mechanisms, corresponding to different chemical conditions, is obtained. At each timestep of the numerical simulation, then, the local thermochemical space (described by the vector
![]() $ \mathbf{y} $
of temperature and chemical species of each cell) is classified by means of a supervised algorithm. Therefore, on the basis of the similarity evaluation between the aforementioned local thermochemical state and the training clusters, one of the reduced mechanisms contained in the library is selected to carry out the reactive step of the ODE integration. This last, on-the-fly, step can be carried out using the Principal Component Analysis (PCA) reconstruction error as in D’Alessio et al. (Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b, Reference D’Alessio, Parente, Stagni and Cuoci2020c), or, alternatively, any other supervised classification algorithm. The SPARC approach can be particularly effective when employed in practical applications where several CFD simulations of the same reactive system, but in different conditions, have to be implemented. This is true, for instance, in process optimization and other parametric studies (in which the Reynolds number can vary) or in the design phase of gas turbines, burners, or chemical reactors (in which different geometrical configurations can be adopted, e.g., different nozzle shapes, inclusion of bluff bodies, etc.). Thus, in these occasions, a possible strategy to reduce the simulation cost is to run a single CFD simulation with detailed kinetics at a low Reynolds number (in light of the relation between the inlet velocity and the computational cost of the simulation) or in steady conditions, and then use the data to train the SPARC approach to adaptively simulate the high Reynolds or the unsteady case. Additional information regarding the inclusion of the SPARC adaptive chemistry in the numerical solver and the resolution of the governing equations can be found in D’Alessio et al. (Reference D’Alessio, Parente, Stagni and Cuoci2020c).
$ \mathbf{y} $
of temperature and chemical species of each cell) is classified by means of a supervised algorithm. Therefore, on the basis of the similarity evaluation between the aforementioned local thermochemical state and the training clusters, one of the reduced mechanisms contained in the library is selected to carry out the reactive step of the ODE integration. This last, on-the-fly, step can be carried out using the Principal Component Analysis (PCA) reconstruction error as in D’Alessio et al. (Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b, Reference D’Alessio, Parente, Stagni and Cuoci2020c), or, alternatively, any other supervised classification algorithm. The SPARC approach can be particularly effective when employed in practical applications where several CFD simulations of the same reactive system, but in different conditions, have to be implemented. This is true, for instance, in process optimization and other parametric studies (in which the Reynolds number can vary) or in the design phase of gas turbines, burners, or chemical reactors (in which different geometrical configurations can be adopted, e.g., different nozzle shapes, inclusion of bluff bodies, etc.). Thus, in these occasions, a possible strategy to reduce the simulation cost is to run a single CFD simulation with detailed kinetics at a low Reynolds number (in light of the relation between the inlet velocity and the computational cost of the simulation) or in steady conditions, and then use the data to train the SPARC approach to adaptively simulate the high Reynolds or the unsteady case. Additional information regarding the inclusion of the SPARC adaptive chemistry in the numerical solver and the resolution of the governing equations can be found in D’Alessio et al. (Reference D’Alessio, Parente, Stagni and Cuoci2020c).
If the chemical mechanism consists of a large number of species (i.e., if the thermochemical space is high-dimensional), the supervised classification can be a difficult task to accomplish, especially if the label assignment is based on the computation of a generic
![]() $ {L}_k $
-norm (as with LPCA). In fact, as also mathematically proved in Aggarwal et al. (Reference Aggarwal, Hinneburg, Keim, van den Bussche and Vianu2001) and Verleysen et al. (Reference Verleysen, Francois, Simon and Wertz2003), as the number of dimensions increases, the concepts of distance and nearest neighbors both lose meaningfulness. Thus, Artificial Neural Networks (ANNs) represent a valid alternative to improve the classification efficiency when dealing with high-dimensional spaces, and they have also already been successfully exploited for combustion and chemical kinetics applications (Christo et al., Reference Christo, Masri, Nebot and Turanyi1995, Reference Christo, Masri, Nebot and Pope1996; Blasco et al., Reference Blasco, Fueyo, Dopazo and Ballester1998; Hao et al., Reference Hao, Kefa and Jianbo2001; Galindo et al., Reference Galindo, Lujan, Serrano and Hernández2005; Chen et al., Reference Chen, Iavarone, Ghiasi, Kannan, D’Alessio, Parente and Swaminathan2020; Dalakoti et al., Reference Dalakoti, Wehrfritz, Savard, Day, Bell and Hawkes2020; Debiagi et al., Reference Debiagi, Nicolai, Han, Janicka and Hasse2020; Angelilli et al., Reference Angelilli, Ciottoli, Malpica Galassi, Hernandez Perez, Soldan, Lu, Valorani and Im2021). ANNs have also been introduced in the context of Large Eddy Simulations of reactive flows in Ihme et al. (Reference Ihme, Schmitt and Pitsch2009), and the comparison with conventional tabulation techniques for chemistry representation led to excellent results in terms of accuracy. Nevertheless, the network performances can also be undermined if the training dataset consists of a large number of features. As described in Bellman (Reference Bellman1961) and Priddy and Keller (Reference Priddy and Keller2005), the number of statistical observations which are necessary to properly train the network is proportional to the input space’s dimensions, following an exponential relation. In light of this problem, one possible solution is to carry out a feature extraction (FE) step prior to the ANN classification. Encoding the input space in a lower dimensional manifold allows to significantly lower the number of features (and, consequently, the number of observations required to properly train the network), at the same time removing the data noise, and eventually increasing the classification accuracy modifying the hyperspace geometry (i.e., promoting the separation between classes). The described combination between FE and classification is nowadays widely used in many scientific applications and domains, such as images classification (Chen et al., Reference Chen, Lin, Zhao, Wang and Gu2014, Reference Chen, Jiang, Li, Jia and Ghamisi2016; Xing et al., Reference Xing, Ma and Yang2016; Zhao and Du, Reference Zhao and Du2016), computational biology (Ongun et al., Reference Ongun, Halici, Leblebicioglu, Atalay, Beksaç and Beksaç2001; Wang et al., Reference Wang, You, Chen, Xia, Liu, Yan, Zhou and Song2018), medical sciences (Alexakis et al., Reference Alexakis, Nyongesa, Saatchi, Harris, Davies, Emery, Ireland and Heller2003; Rafiuddin et al., Reference Rafiuddin, Khan and Farooq2011; Kottaimalai et al., Reference Kottaimalai, Rajasekaran, Selvam and Kannapiran2013), and fault detection identification (Thirukovalluru et al., Reference Thirukovalluru, Dixit, Sevakula, Verma and Salour2016; Vartouni et al., Reference Vartouni, Kashi and Teshnehlab2018).
$ {L}_k $
-norm (as with LPCA). In fact, as also mathematically proved in Aggarwal et al. (Reference Aggarwal, Hinneburg, Keim, van den Bussche and Vianu2001) and Verleysen et al. (Reference Verleysen, Francois, Simon and Wertz2003), as the number of dimensions increases, the concepts of distance and nearest neighbors both lose meaningfulness. Thus, Artificial Neural Networks (ANNs) represent a valid alternative to improve the classification efficiency when dealing with high-dimensional spaces, and they have also already been successfully exploited for combustion and chemical kinetics applications (Christo et al., Reference Christo, Masri, Nebot and Turanyi1995, Reference Christo, Masri, Nebot and Pope1996; Blasco et al., Reference Blasco, Fueyo, Dopazo and Ballester1998; Hao et al., Reference Hao, Kefa and Jianbo2001; Galindo et al., Reference Galindo, Lujan, Serrano and Hernández2005; Chen et al., Reference Chen, Iavarone, Ghiasi, Kannan, D’Alessio, Parente and Swaminathan2020; Dalakoti et al., Reference Dalakoti, Wehrfritz, Savard, Day, Bell and Hawkes2020; Debiagi et al., Reference Debiagi, Nicolai, Han, Janicka and Hasse2020; Angelilli et al., Reference Angelilli, Ciottoli, Malpica Galassi, Hernandez Perez, Soldan, Lu, Valorani and Im2021). ANNs have also been introduced in the context of Large Eddy Simulations of reactive flows in Ihme et al. (Reference Ihme, Schmitt and Pitsch2009), and the comparison with conventional tabulation techniques for chemistry representation led to excellent results in terms of accuracy. Nevertheless, the network performances can also be undermined if the training dataset consists of a large number of features. As described in Bellman (Reference Bellman1961) and Priddy and Keller (Reference Priddy and Keller2005), the number of statistical observations which are necessary to properly train the network is proportional to the input space’s dimensions, following an exponential relation. In light of this problem, one possible solution is to carry out a feature extraction (FE) step prior to the ANN classification. Encoding the input space in a lower dimensional manifold allows to significantly lower the number of features (and, consequently, the number of observations required to properly train the network), at the same time removing the data noise, and eventually increasing the classification accuracy modifying the hyperspace geometry (i.e., promoting the separation between classes). The described combination between FE and classification is nowadays widely used in many scientific applications and domains, such as images classification (Chen et al., Reference Chen, Lin, Zhao, Wang and Gu2014, Reference Chen, Jiang, Li, Jia and Ghamisi2016; Xing et al., Reference Xing, Ma and Yang2016; Zhao and Du, Reference Zhao and Du2016), computational biology (Ongun et al., Reference Ongun, Halici, Leblebicioglu, Atalay, Beksaç and Beksaç2001; Wang et al., Reference Wang, You, Chen, Xia, Liu, Yan, Zhou and Song2018), medical sciences (Alexakis et al., Reference Alexakis, Nyongesa, Saatchi, Harris, Davies, Emery, Ireland and Heller2003; Rafiuddin et al., Reference Rafiuddin, Khan and Farooq2011; Kottaimalai et al., Reference Kottaimalai, Rajasekaran, Selvam and Kannapiran2013), and fault detection identification (Thirukovalluru et al., Reference Thirukovalluru, Dixit, Sevakula, Verma and Salour2016; Vartouni et al., Reference Vartouni, Kashi and Teshnehlab2018).
In this work, a novel on-the-fly classifier based on FE and ANN is proposed to adaptively simulate laminar coflow diffusion flames fed with a nitrogen-diluted n-heptane stream in air. The new classifier performances are firstly compared a posteriori with a PCA-based classifier and an s-ANN classifier (without the FE step) in terms of speed-up and accuracy in the description of Polycyclic Aromatic Hydrocarbon (PAH) species with respect with the detailed one. Finally, the new classifier is tested on three flames with different boundary conditions (BCs; in terms of Reynolds number, or using unsteady BCs) with respect to the one used for the training.
The remainder of the paper is structured as follows: in Section 2, the classification algorithms are explained in detail, and a step-by-step procedure for the on-the-fly classification is shown; in Section 3, the numerical setup for the CFD simulations is described; in Section 4, the adaptive simulation results for the four flames are shown and discussed.
2. Theory
2.1. Algorithms for the on-the-fly classification
2.1.1. Clustering and classification via local principal component analysis
In this work, PCA is used to identify a lower-dimensional manifold spanned by a new set of orthogonal directions explaining nearly all the variance contained in the original dataset
![]() $ \mathbf{X}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, consisting of
$ \mathbf{X}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, consisting of
![]() $ n $
statistical observations of
$ n $
statistical observations of
![]() $ p $
variables. Mathematically speaking, the new directions are represented by a set of eigenvectors
$ p $
variables. Mathematically speaking, the new directions are represented by a set of eigenvectors
![]() $ \mathbf{A}\in {\mathrm{\mathbb{R}}}^{p\times p} $
obtained by the eigendecomposition of the covariance matrix
$ \mathbf{A}\in {\mathrm{\mathbb{R}}}^{p\times p} $
obtained by the eigendecomposition of the covariance matrix
![]() $ \mathbf{S}\in {\mathrm{\mathbb{R}}}^{p\times p} $
:
$ \mathbf{S}\in {\mathrm{\mathbb{R}}}^{p\times p} $
:
The basis can be truncated to retain only the relevant information contained in the first
![]() $ q $
eigenvectors, and the matrix
$ q $
eigenvectors, and the matrix
![]() $ {\mathbf{A}}_{\mathbf{q}}\in {\mathrm{\mathbb{R}}}^{p\times q} $
is obtained. Projecting the original data matrix on
$ {\mathbf{A}}_{\mathbf{q}}\in {\mathrm{\mathbb{R}}}^{p\times q} $
is obtained. Projecting the original data matrix on
![]() $ {\mathbf{A}}_{\mathbf{q}} $
, the matrix of the truncated scores,
$ {\mathbf{A}}_{\mathbf{q}} $
, the matrix of the truncated scores,
![]() $ {\mathbf{Z}}_{\mathbf{q}}\in {\mathrm{\mathbb{R}}}^{n\times q} $
, is obtained:
$ {\mathbf{Z}}_{\mathbf{q}}\in {\mathrm{\mathbb{R}}}^{n\times q} $
, is obtained:
Because of the eigenvectors’ matrix orthonormality, i.e.,
![]() $ {{\mathbf{A}}_{\mathbf{q}}}^{-1}={{\mathbf{A}}_{\mathbf{q}}}^T $
, it is possible to approximate the original dataset from the reduced PCA manifold by means of a matrix multiplication:
$ {{\mathbf{A}}_{\mathbf{q}}}^{-1}={{\mathbf{A}}_{\mathbf{q}}}^T $
, it is possible to approximate the original dataset from the reduced PCA manifold by means of a matrix multiplication:
The difference between the original and the reconstructed set of observations is the PCA reconstruction error, and it is defined as
LPCA with vector quantization, introduced in Kambhatla and Leen (Reference Kambhatla and Leen1997), is a piecewise-linear formulation of PCA that extends its applicability also to nonlinear cases, reducing the error due to the linearity of the original, global, algorithm. This unsupervised algorithm uses the minimization of the reconstruction error reported in Equation (4) as objective function, partitioning the matrix
![]() $ \mathbf{X} $
in
$ \mathbf{X} $
in
![]() $ k $
clusters, and separately performing a dimensionality reduction in each of them. Given that,
$ k $
clusters, and separately performing a dimensionality reduction in each of them. Given that,
![]() $ k $
eigenvector matrices
$ k $
eigenvector matrices
![]() $ {\mathbf{A}}_{\mathbf{q}\hskip1.5pt j}, $
with
$ {\mathbf{A}}_{\mathbf{q}\hskip1.5pt j}, $
with
![]() $ j=1,\dots, k $
, are found at each iteration, and the observations of the dataset
$ j=1,\dots, k $
, are found at each iteration, and the observations of the dataset
![]() $ \mathbf{X} $
are assigned to the cluster
$ \mathbf{X} $
are assigned to the cluster
![]() $ \overline{k} $
such that:
$ \overline{k} $
such that:
Additional information regarding the iterative algorithm can be found in Kambhatla and Leen (Reference Kambhatla and Leen1997) and D’Alessio et al. (Reference D’Alessio, Attili, Cuoci, Pitsch and Parente2020a, Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b, Reference D’Alessio, Parente, Stagni and Cuoci2020c).
As also proved in Kambhatla and Leen (Reference Kambhatla and Leen1997), the local reconstruction error reported in Equation (6) can be seen as the Euclidean orthogonal distance between the considered observation and the reduced manifold spanned by the set of eigenvectors of the jth cluster,
![]() $ {\mathbf{A}}_{\mathbf{q}\hskip1.5pt j}. $
This partitioning criterion has already shown its potential in the field of combustion for both dimensionality reduction (Parente et al., Reference Parente, Sutherland, Tognotti and Smith2009, Reference Parente, Sutherland, Dally, Tognotti and Smith2011) and clustering (D’Alessio et al., Reference D’Alessio, Attili, Cuoci, Pitsch and Parente2020a, Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b, Reference D’Alessio, Parente, Stagni and Cuoci2020c) tasks, and it has also proved to be competitive with other state-of-the-art clustering algorithms (D’Alessio et al., Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b).
$ {\mathbf{A}}_{\mathbf{q}\hskip1.5pt j}. $
This partitioning criterion has already shown its potential in the field of combustion for both dimensionality reduction (Parente et al., Reference Parente, Sutherland, Tognotti and Smith2009, Reference Parente, Sutherland, Dally, Tognotti and Smith2011) and clustering (D’Alessio et al., Reference D’Alessio, Attili, Cuoci, Pitsch and Parente2020a, Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b, Reference D’Alessio, Parente, Stagni and Cuoci2020c) tasks, and it has also proved to be competitive with other state-of-the-art clustering algorithms (D’Alessio et al., Reference D’Alessio, Cuoci, Aversano, Bracconi, Stagni and Parente2020b).
The objective function reported in Equation (6) can also be used to classify a new, unobserved, point, on the basis of a previous dataset partitioning. In fact, given a training dataset
![]() $ \tilde{\mathbf{X}}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, centered and scaled with its centering and scaling factors
$ \tilde{\mathbf{X}}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, centered and scaled with its centering and scaling factors
![]() $ {\boldsymbol{\mu}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
and
$ {\boldsymbol{\mu}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
and
![]() $ {\boldsymbol{\sigma}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
, partitioned in
$ {\boldsymbol{\sigma}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
, partitioned in
![]() $ k $
clusters via LPCA, it is possible to classify a new, unobserved, vector
$ k $
clusters via LPCA, it is possible to classify a new, unobserved, vector
![]() $ \mathbf{y}\in {\mathrm{\mathbb{R}}}^{1\times p} $
by means of the following procedure:
$ \mathbf{y}\in {\mathrm{\mathbb{R}}}^{1\times p} $
by means of the following procedure:
-
1. Centering and scaling: The new observation
 $ \mathbf{y} $
is centered and scaled with
$ \mathbf{y} $
is centered and scaled with
 $ {\boldsymbol{\mu}}_{\boldsymbol{x}} $
and
$ {\boldsymbol{\mu}}_{\boldsymbol{x}} $
and
 $ {\boldsymbol{\sigma}}_{\boldsymbol{x}} $
, the centering and scaling factors of the training dataset. The centered and scaled vector
$ {\boldsymbol{\sigma}}_{\boldsymbol{x}} $
, the centering and scaling factors of the training dataset. The centered and scaled vector
 $ \tilde{\mathbf{y}} $
is obtained after this operation;
$ \tilde{\mathbf{y}} $
is obtained after this operation; -
2. Projection: The vector
 $ \tilde{\mathbf{y}} $
is projected on the
$ \tilde{\mathbf{y}} $
is projected on the
 $ k $
local, lower-dimensional, manifolds spanned by the local PCs (
$ k $
local, lower-dimensional, manifolds spanned by the local PCs (
 $ {\mathbf{A}}_{\mathbf{q}\hskip1.5pt j} $
) using Equation (3);
$ {\mathbf{A}}_{\mathbf{q}\hskip1.5pt j} $
) using Equation (3); -
3. Cluster assignment: The
 $ k $
projections are reconstructed using the local eigenvectors, and the associated reconstruction error is computed (Equations (4) and (5)). The considered observation is thus assigned to the cluster
$ k $
projections are reconstructed using the local eigenvectors, and the associated reconstruction error is computed (Equations (4) and (5)). The considered observation is thus assigned to the cluster
 $ \overline{k} $
, which minimizes the reconstruction error (Equation (6)).
$ \overline{k} $
, which minimizes the reconstruction error (Equation (6)).
2.1.2. Classification via artificial neural networks
ANNs are universal function approximators (Hornik et al., Reference Hornik, Stinchcombe and White1989; Stinchcombe and White, Reference Stinchcombe and White1989; Hornik, Reference Hornik1991), which can be used for regression or classification tasks (Specht, Reference Specht1991; Dreiseitl and Ohno-Machado, Reference Dreiseitl and Ohno-Machado2002). They consist of a series of interconnected layers, each layer being characterized by a certain number of nodes, or neurons.
Given an input vector
![]() $ \mathbf{x}\in {\mathrm{\mathbb{R}}}^{1\times p} $
to the network, it is linearly combined with the weights
$ \mathbf{x}\in {\mathrm{\mathbb{R}}}^{1\times p} $
to the network, it is linearly combined with the weights
![]() $ \mathbf{W} $
and the biases
$ \mathbf{W} $
and the biases
![]() $ \mathbf{b} $
of the first layer, and it is then activated by a nonlinear function h(
$ \mathbf{b} $
of the first layer, and it is then activated by a nonlinear function h(
![]() $ \cdot $
):
$ \cdot $
):
After that,
![]() $ \mathbf{z} $
undergoes the same linear combination of the immediately following layer’s weights and biases, with a subsequent nonlinear activation, until the last layer, that is, the output layer, is reached (Bishop, Reference Bishop2006). The layers between the input and the output are called hidden layers (HLs): if the network architecture is characterized by two or more HLs, the neural network can be defined deep. During the network training phase, the numerical values of the weights are modified at each iteration (epoch) to better approximate the output function, in case of regression, or to have a better accuracy in the class prediction, in case of classification tasks, by means of the backpropagation algorithm (Hecht-Nielsen, Reference Hecht-Nielsen1992; Bishop, Reference Bishop2006). The possibility to use a nonlinear activation function is the real strength of this method, allowing the architecture to learn complex patterns hidden in the data (Stinchcombe and White, Reference Stinchcombe and White1989).
$ \mathbf{z} $
undergoes the same linear combination of the immediately following layer’s weights and biases, with a subsequent nonlinear activation, until the last layer, that is, the output layer, is reached (Bishop, Reference Bishop2006). The layers between the input and the output are called hidden layers (HLs): if the network architecture is characterized by two or more HLs, the neural network can be defined deep. During the network training phase, the numerical values of the weights are modified at each iteration (epoch) to better approximate the output function, in case of regression, or to have a better accuracy in the class prediction, in case of classification tasks, by means of the backpropagation algorithm (Hecht-Nielsen, Reference Hecht-Nielsen1992; Bishop, Reference Bishop2006). The possibility to use a nonlinear activation function is the real strength of this method, allowing the architecture to learn complex patterns hidden in the data (Stinchcombe and White, Reference Stinchcombe and White1989).
Although ANNs are a powerful tool to be used for regression and classification problems, they result to be prone to overfitting. For this reason, several methods and strategies have been formulated to stem this phenomenon, such as dropout and early stopping (Caruana et al., Reference Caruana, Lawrence and Giles2001; Srivastava et al., Reference Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov2014). In particular, early stopping is an effective tool to deal with situations in which the networks would tend to overfit, as it stops the training in advance, when the learned model is similar to the one that would have been achieved by an optimal-sized architecture (Caruana et al., Reference Caruana, Lawrence and Giles2001).
Supposing to have a training dataset
![]() $ \tilde{\mathbf{X}}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, centered and scaled with its centering and scaling factors
$ \tilde{\mathbf{X}}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, centered and scaled with its centering and scaling factors
![]() $ {\boldsymbol{\mu}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
and
$ {\boldsymbol{\mu}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
and
![]() $ {\boldsymbol{\sigma}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
, partitioned in
$ {\boldsymbol{\sigma}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
, partitioned in
![]() $ k $
clusters, the classification of a new, unobserved, vector
$ k $
clusters, the classification of a new, unobserved, vector
![]() $ \mathbf{y}\in {\mathrm{\mathbb{R}}}^{1\times p} $
is, in this case, accomplished according to the following steps:
$ \mathbf{y}\in {\mathrm{\mathbb{R}}}^{1\times p} $
is, in this case, accomplished according to the following steps:
-
1. Centering and scaling: The new observation
 $ \mathbf{y} $
is centered and scaled with
$ \mathbf{y} $
is centered and scaled with
 $ {\boldsymbol{\mu}}_{\boldsymbol{x}} $
and
$ {\boldsymbol{\mu}}_{\boldsymbol{x}} $
and
 $ {\boldsymbol{\sigma}}_{\boldsymbol{x}} $
, the centering and the scaling factors of the networks’ training dataset. The centered and scaled vector
$ {\boldsymbol{\sigma}}_{\boldsymbol{x}} $
, the centering and the scaling factors of the networks’ training dataset. The centered and scaled vector
 $ \tilde{\mathbf{y}} $
is obtained after this operation;
$ \tilde{\mathbf{y}} $
is obtained after this operation; -
2. Forward pass through the network: The centered and scaled observation
 $ \tilde{\mathbf{y}} $
has a forward pass through the trained network;
$ \tilde{\mathbf{y}} $
has a forward pass through the trained network; -
3. Cluster assignment: The observation is assigned to the class which maximizes the membership probability, computed applying a softmax function on the output layer.
2.2. Classification via feature extraction and artificial neural networks
If the training data fed to any machine learning algorithm are high-dimensional, it is very likely that many of the input variables are redundant, therefore adding a large amount of noisy information. This aspect is inconvenient from a model development perspective, as it makes difficult to achieve a valuable knowledge discovery process, as well as from a predictive modeling point of view, because of the highly exponential relation between the number of features and the number of statistical observations required to properly train the model (Priddy and Keller, Reference Priddy and Keller2005). FE algorithms were thus designed to find a new, lower-dimensional, representation of the space which is spanned by the input data (i.e., a new, reduced, set of variables) with minimal information loss. Among all the possible FE techniques, it is worth mentioning PCA (Jolliffe, Reference Jolliffe1986; Bishop, Reference Bishop2006), Independent Component Analysis (Hyvärinen and Oja, Reference Hyvärinen and Oja2000), Non-negative Matrix Factorization (Lee and Seung, Reference Lee, Seung, Leen, Dietterich and Tresp2001), and Dynamic Mode Decomposition (Schmid, Reference Schmid2010; Tu et al., Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2013; Grenga et al., Reference Grenga, MacArt and Mueller2018), among the linear methods, as well as Autoencoders (AEs; Ng, Reference Ng2011), Kernel Principal Component Analysis (KPCA; Mika et al., Reference Mika, Schölkopf, Smola, Müller, Scholz and Rätsch1999; Rosipal et al., Reference Rosipal, Girolami, Trejo and Cichocki2001; Mirgolbabaei et al., Reference Mirgolbabaei, Echekki and Smaoui2014), Isomap (IM; Choi and Choi, Reference Choi and Choi2007; Bansal et al., Reference Bansal, Mascarenhas and Chen2011), and t-distributed Stochastic Neighbor Embedding (t-SNE; van der Maaten and Hinton, Reference van der Maaten and Hinton2008; Fooladgar and Duwig, Reference Fooladgar and Duwig2018), among the nonlinear methods. Because of the intrinsic nonlinearity characterizing both fluid dynamics and chemical kinetics, the application of nonlinear FE methods would obviously be more suitable for combustion applications, but their application is not always straightforward. In fact, methods based on the computation of a kernel matrix (
![]() $ \mathbf{K} $
) and its relative decomposition (e.g., KPCA and IM) are computationally expensive. As a result, they can be applied only to relatively small training matrices (accounting for thousands of statistical observations, maximum), as the storage of
$ \mathbf{K} $
) and its relative decomposition (e.g., KPCA and IM) are computationally expensive. As a result, they can be applied only to relatively small training matrices (accounting for thousands of statistical observations, maximum), as the storage of
![]() $ \mathbf{K} $
requires
$ \mathbf{K} $
requires
![]() $ O\left({n}^2\right) $
space, and its computation
$ O\left({n}^2\right) $
space, and its computation
![]() $ O\left({n}^2d\right) $
operations, where
$ O\left({n}^2d\right) $
operations, where
![]() $ n $
is the number of statistical observations of the training matrix, and
$ n $
is the number of statistical observations of the training matrix, and
![]() $ d $
the number of its variables (Si et al., Reference Si, Hsieh and Dhillon2017). On the other hand, methods such as AE and t-SNE require a remarkable user expertise and a thorough sensitivity analysis to find the optimal setting of the hyperparameters, as poor results are obtained otherwise. Linear FE methods are, instead, faster from a computational point of view, and straightforward to use (because of the lower number of hyperparameters to be set) with respect to the aforementioned, nonlinear, ones. In particular, among all the aforementioned linear FE algorithms, PCA, despite its linear nature, has proved to be a valuable tool to extract the main features for combustion datasets, and its use is well documented in literature for model order reduction in reactive flow applications (Parente et al., Reference Parente, Sutherland, Tognotti and Smith2009, Reference Parente, Sutherland, Dally, Tognotti and Smith2011; Isaac et al., Reference Isaac, Coussement, Gicquel, Smith and Parente2014; Aversano et al., Reference Aversano, Bellemans, Li, Coussement, Gicquel and Parente2019).
$ d $
the number of its variables (Si et al., Reference Si, Hsieh and Dhillon2017). On the other hand, methods such as AE and t-SNE require a remarkable user expertise and a thorough sensitivity analysis to find the optimal setting of the hyperparameters, as poor results are obtained otherwise. Linear FE methods are, instead, faster from a computational point of view, and straightforward to use (because of the lower number of hyperparameters to be set) with respect to the aforementioned, nonlinear, ones. In particular, among all the aforementioned linear FE algorithms, PCA, despite its linear nature, has proved to be a valuable tool to extract the main features for combustion datasets, and its use is well documented in literature for model order reduction in reactive flow applications (Parente et al., Reference Parente, Sutherland, Tognotti and Smith2009, Reference Parente, Sutherland, Dally, Tognotti and Smith2011; Isaac et al., Reference Isaac, Coussement, Gicquel, Smith and Parente2014; Aversano et al., Reference Aversano, Bellemans, Li, Coussement, Gicquel and Parente2019).
The coupling between the FE and the ANN classification is accomplished by prefixing the PCA step to the network classification, i.e., feeding and training the network with the lower-dimensional projection of the training matrix (i.e., with the scores matrix
![]() $ {\mathbf{Z}}_{\mathbf{q}} $
). A general scheme of the encoding-classification procedure is shown in Figure 1.
$ {\mathbf{Z}}_{\mathbf{q}} $
). A general scheme of the encoding-classification procedure is shown in Figure 1.

Figure 1. Operational diagram of the on-the-fly classifier based on feature extraction (FE) and ANN: an FE step (encoding) is carried out by means of principal component analysis, and the lower-dimensional data representation is fed to the ANN for the classification.
Given a training dataset
![]() $ \tilde{\mathbf{X}}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, centered and scaled with its centering and scaling factors
$ \tilde{\mathbf{X}}\in {\mathrm{\mathbb{R}}}^{n\times p} $
, centered and scaled with its centering and scaling factors
![]() $ {\boldsymbol{\mu}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
and
$ {\boldsymbol{\mu}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
and
![]() $ {\boldsymbol{\sigma}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
, partitioned in
$ {\boldsymbol{\sigma}}_{\boldsymbol{x}}\in {\mathrm{\mathbb{R}}}^{1\times p} $
, partitioned in
![]() $ k $
clusters, to whom PCA has been applied (i.e., the eigenvectors matrix
$ k $
clusters, to whom PCA has been applied (i.e., the eigenvectors matrix
![]() $ {\mathbf{A}}_{\mathbf{q}}\in {\mathrm{\mathbb{R}}}^{p\times q} $
has been retrieved), it is possible to classify a new, unobserved, vector
$ {\mathbf{A}}_{\mathbf{q}}\in {\mathrm{\mathbb{R}}}^{p\times q} $
has been retrieved), it is possible to classify a new, unobserved, vector
![]() $ \mathbf{y}\in {\mathrm{\mathbb{R}}}^{1\times p} $
on the basis of the aforementioned partitioning by means of the following procedure:
$ \mathbf{y}\in {\mathrm{\mathbb{R}}}^{1\times p} $
on the basis of the aforementioned partitioning by means of the following procedure:
-
1. Centering and scaling: The new observation
 $ \mathbf{y} $
is centered and scaled with
$ \mathbf{y} $
is centered and scaled with
 $ {\boldsymbol{\mu}}_{\boldsymbol{x}} $
and
$ {\boldsymbol{\mu}}_{\boldsymbol{x}} $
and
 $ {\boldsymbol{\sigma}}_{\boldsymbol{x}} $
, the centering and scaling factors of the training dataset. The centered and scaled vector
$ {\boldsymbol{\sigma}}_{\boldsymbol{x}} $
, the centering and scaling factors of the training dataset. The centered and scaled vector
 $ \tilde{\mathbf{y}} $
is obtained after this operation;
$ \tilde{\mathbf{y}} $
is obtained after this operation; -
2. Encoding: The vector
 $ \tilde{\mathbf{y}} $
is projected on the reduced manifold spanned by the eigenvectors’ matrix
$ \tilde{\mathbf{y}} $
is projected on the reduced manifold spanned by the eigenvectors’ matrix
 $ {\mathbf{A}}_{\mathbf{q}} $
, by means of the matrix multiplication
$ {\mathbf{A}}_{\mathbf{q}} $
, by means of the matrix multiplication
 $ {\mathbf{z}}_{\mathbf{q}}=\tilde{\mathbf{y}}{\mathbf{A}}_{\mathbf{q}} $
. Thus, at the end of this step, the PC-score vector
$ {\mathbf{z}}_{\mathbf{q}}=\tilde{\mathbf{y}}{\mathbf{A}}_{\mathbf{q}} $
. Thus, at the end of this step, the PC-score vector
 $ {\mathbf{z}}_{\mathbf{q}} $
is obtained;
$ {\mathbf{z}}_{\mathbf{q}} $
is obtained; -
3. Forward pass through the network: The PC-score vector
 $ {\mathbf{z}}_{\mathbf{q}} $
has a forward pass through the trained network;
$ {\mathbf{z}}_{\mathbf{q}} $
has a forward pass through the trained network; -
4. Cluster assignment: The observation is assigned to the class which maximizes the membership probability, computed applying a softmax function on the output layer.
3. Case Description
The first configuration chosen to test the adaptive chemistry methodology here presented is an axisymmetric, steady, nonpremixed laminar nitrogen-diluted n-heptane coflow flame. The fuel stream is injected at 400 K with the following composition on molar basis:
![]() $ \mathrm{n}\hbox{-} {\mathrm{C}}_7{\mathrm{H}}_{16}/{\mathrm{N}}_2=0.35/0.65 $
. The oxidizer stream, consisting of regular air, is injected at 300 K. The fuel enters through a circular nozzle (internal diameter of 11 mm and thickness of 0.90 mm), whereas the oxidizer enters through an annular region (internal diameter of 50 mm). The velocity profile of the fuel stream is imposed parabolic at the boundary, following the equation:
$ \mathrm{n}\hbox{-} {\mathrm{C}}_7{\mathrm{H}}_{16}/{\mathrm{N}}_2=0.35/0.65 $
. The oxidizer stream, consisting of regular air, is injected at 300 K. The fuel enters through a circular nozzle (internal diameter of 11 mm and thickness of 0.90 mm), whereas the oxidizer enters through an annular region (internal diameter of 50 mm). The velocity profile of the fuel stream is imposed parabolic at the boundary, following the equation:
 $$ v(r)=2{v}_m\left(1-\frac{r^2}{R^2}\right), $$
$$ v(r)=2{v}_m\left(1-\frac{r^2}{R^2}\right), $$
where r is the radial coordinate, R the internal radius, and
![]() $ {v}_m $
is equal to 10.12
$ {v}_m $
is equal to 10.12
![]() $ cm/s $
. The coflow air is injected instead with constant velocity equal to 12.32
$ cm/s $
. The coflow air is injected instead with constant velocity equal to 12.32
![]() $ cm/s $
. The burner geometry and the inlet velocities are the same adopted in Kashif et al. (Reference Kashif, Bonnety, Matynia, Da Costa and Legros2015) to study the propensity to soot formation of gasoline surrogates. The numerical simulations were carried out with the laminarSMOKE code, a CFD solver based on OpenFOAM and specifically conceived for laminar reacting flows with detailed kinetic mechanismsFootnote
1
(Cuoci et al., Reference Cuoci, Frassoldati, Faravelli and Ranzi2013). The 2D computational domain (with lengths of 40 and 100 mm in the radial and axial directions, respectively) was discretized through a Cartesian mesh with a total number of ~10,000 cells, more refined in the nozzle proximity and in the reactive zone, after a mesh sensitivity and convergence study. The simulations were carried out using the POLIMI_PRF_PAH_HT_1412 kinetic mechanism (172 species and 6,067 reactions): this mechanism accounts for the pyrolysis, the partial oxidation, and the combustion of n-heptane, also including the chemistry of PAHs up to C
$ cm/s $
. The burner geometry and the inlet velocities are the same adopted in Kashif et al. (Reference Kashif, Bonnety, Matynia, Da Costa and Legros2015) to study the propensity to soot formation of gasoline surrogates. The numerical simulations were carried out with the laminarSMOKE code, a CFD solver based on OpenFOAM and specifically conceived for laminar reacting flows with detailed kinetic mechanismsFootnote
1
(Cuoci et al., Reference Cuoci, Frassoldati, Faravelli and Ranzi2013). The 2D computational domain (with lengths of 40 and 100 mm in the radial and axial directions, respectively) was discretized through a Cartesian mesh with a total number of ~10,000 cells, more refined in the nozzle proximity and in the reactive zone, after a mesh sensitivity and convergence study. The simulations were carried out using the POLIMI_PRF_PAH_HT_1412 kinetic mechanism (172 species and 6,067 reactions): this mechanism accounts for the pyrolysis, the partial oxidation, and the combustion of n-heptane, also including the chemistry of PAHs up to C
![]() $ {}_{20} $
. Extensive validation and detailed description of such mechanism can be found in Pelucchi et al. (Reference Pelucchi, Bissoli, Cavallotti, Cuoci, Faravelli, Frassoldati, Ranzi and Stagni2014).
$ {}_{20} $
. Extensive validation and detailed description of such mechanism can be found in Pelucchi et al. (Reference Pelucchi, Bissoli, Cavallotti, Cuoci, Faravelli, Frassoldati, Ranzi and Stagni2014).
Three additional flame configurations, obtained imposing different BCs, were considered for the validation of the adaptive approach using the proposed on-the-fly classifier, of which one in steady conditions, and two in unsteady conditions. The steady test flame was obtained using the same BCs as the first one but the Reynolds number: the inlet velocity profile was, in fact, set to 20.24
![]() $ cm/s $
, thus doubling the Reynolds number. The two unsteady test flames were obtained imposing a sinusoidal perturbation with prescribed frequency
$ cm/s $
, thus doubling the Reynolds number. The two unsteady test flames were obtained imposing a sinusoidal perturbation with prescribed frequency
![]() $ f $
and amplitude
$ f $
and amplitude
![]() $ A $
to the parabolic inlet velocity profile, as shown in Equation (9). The frequencies and the amplitudes imposed to the flames to obtain the unsteady behavior were selected verifying their effectiveness a posteriori, that is, verifying that the sinusoidal perturbations with prescribed frequency and amplitudes were able to dynamically modify the thermochemical field of the flame, with respect to the steady solution. A more detailed and general study regarding the applicability and the effects of different perturbations in the context of the SPARC adaptive chemistry approach was already extensively carried out by the authors in D’Alessio et al. (Reference D’Alessio, Parente, Stagni and Cuoci2020c).
$ A $
to the parabolic inlet velocity profile, as shown in Equation (9). The frequencies and the amplitudes imposed to the flames to obtain the unsteady behavior were selected verifying their effectiveness a posteriori, that is, verifying that the sinusoidal perturbations with prescribed frequency and amplitudes were able to dynamically modify the thermochemical field of the flame, with respect to the steady solution. A more detailed and general study regarding the applicability and the effects of different perturbations in the context of the SPARC adaptive chemistry approach was already extensively carried out by the authors in D’Alessio et al. (Reference D’Alessio, Parente, Stagni and Cuoci2020c).
 $$ v\left(r,t\right)=2{v}_m\left(1-\frac{r^2}{R^2}\right)\left[1+ Asin\left(2\pi ft\right)\right]. $$
$$ v\left(r,t\right)=2{v}_m\left(1-\frac{r^2}{R^2}\right)\left[1+ Asin\left(2\pi ft\right)\right]. $$
The numerical values for the BCs concerning the inlet velocities, as well as the frequencies
![]() $ f $
and the amplitudes
$ f $
and the amplitudes
![]() $ A $
of the sinusoidal perturbations used for the numerical simulations, are summarized in Table 1.
$ A $
of the sinusoidal perturbations used for the numerical simulations, are summarized in Table 1.
Table 1. Flame configurations chosen to test the sample partitioning adaptive reduced chemistry approach: velocity of the fuel inlet parabolic profile (
![]() $ {\mathrm{v}}_{\mathrm{m}} $
), frequency of the sinusoidal perturbation imposed to the fuel parabolic velocity profile (
$ {\mathrm{v}}_{\mathrm{m}} $
), frequency of the sinusoidal perturbation imposed to the fuel parabolic velocity profile (
![]() $ \mathrm{f} $
), and amplitude of the sinusoidal perturbation imposed to the fuel parabolic velocity profile (
$ \mathrm{f} $
), and amplitude of the sinusoidal perturbation imposed to the fuel parabolic velocity profile (
![]() $ \mathrm{A} $
).
$ \mathrm{A} $
).

4. Results
4.1. Prepartitioning of composition space and reduced mechanism generation
The generation of the reduced mechanisms to be used in the multidimensional adaptive simulations was obtained prepartitioning the thermochemical space spanned by the S1 dataset with LPCA, using
![]() $ 25 $
PCs. The training data consisted of ~170,000 statistical observations of 173 variables (temperature and the 172 chemical species included in the detailed kinetic mechanism), and they were centered with their mean values and scaled with their standard deviations. With regard to the second hyperparameter of the LPCA algorithm, i.e., the number of clusters to be used for the partitioning of the thermochemical space, it was set equal to 7 according to the minimization of the Davies–Bouldin (DB) index (Davies and Bouldin, Reference Davies and Bouldin1979). In fact, in the absence of an a priori knowledge of the optimal number of clusters (from a physical and chemical point of view), the aforementioned index can provide an estimation from a geometric point of view. The LPCA prepartitioning, as well as the choice of the optimal number of clusters by means of the DB index, was accomplished using the OpenMORe framework, an open-source Python tool for clustering, model order reduction, and data analysis.Footnote
2
The reduced chemical mechanisms were initially generated in each cluster using a tolerance
$ 25 $
PCs. The training data consisted of ~170,000 statistical observations of 173 variables (temperature and the 172 chemical species included in the detailed kinetic mechanism), and they were centered with their mean values and scaled with their standard deviations. With regard to the second hyperparameter of the LPCA algorithm, i.e., the number of clusters to be used for the partitioning of the thermochemical space, it was set equal to 7 according to the minimization of the Davies–Bouldin (DB) index (Davies and Bouldin, Reference Davies and Bouldin1979). In fact, in the absence of an a priori knowledge of the optimal number of clusters (from a physical and chemical point of view), the aforementioned index can provide an estimation from a geometric point of view. The LPCA prepartitioning, as well as the choice of the optimal number of clusters by means of the DB index, was accomplished using the OpenMORe framework, an open-source Python tool for clustering, model order reduction, and data analysis.Footnote
2
The reduced chemical mechanisms were initially generated in each cluster using a tolerance
![]() $ {\epsilon}_{DRGEP}=0.005 $
, as done in D’Alessio et al. (Reference D’Alessio, Parente, Stagni and Cuoci2020c). The statistics regarding the chemical reduction for the n-heptane detailed mechanism are reported in Table 2 regarding the mean (
$ {\epsilon}_{DRGEP}=0.005 $
, as done in D’Alessio et al. (Reference D’Alessio, Parente, Stagni and Cuoci2020c). The statistics regarding the chemical reduction for the n-heptane detailed mechanism are reported in Table 2 regarding the mean (
![]() $ {n}_{sp}^{mean} $
) and maximum number of species
$ {n}_{sp}^{mean} $
) and maximum number of species
![]() $ \left({n}_{sp}^{max}\right) $
, as well as for the mean and maximum nonuniformity coefficient (
$ \left({n}_{sp}^{max}\right) $
, as well as for the mean and maximum nonuniformity coefficient (
![]() $ {\lambda}_{mean} $
and
$ {\lambda}_{mean} $
and
![]() $ {\lambda}_{max} $
, respectively). The nonuniformity coefficient
$ {\lambda}_{max} $
, respectively). The nonuniformity coefficient
![]() $ \lambda $
is defined as
$ \lambda $
is defined as
 $$ \lambda =\frac{1}{n_{sp}}\sum \limits_{i=1}^{n_{sp}}{\left({x}_i-1\right)}^2, $$
$$ \lambda =\frac{1}{n_{sp}}\sum \limits_{i=1}^{n_{sp}}{\left({x}_i-1\right)}^2, $$
where
![]() $ {n}_{sp} $
is the total number of species included in the kinetic mechanism. The quantity
$ {n}_{sp} $
is the total number of species included in the kinetic mechanism. The quantity
![]() $ {x}_i $
is defined as
$ {x}_i $
is defined as
 $$ {x}_i=\frac{1}{n_{it}}\sum \limits_{j=1}^{n_{it}}{\delta}_{i,j}, $$
$$ {x}_i=\frac{1}{n_{it}}\sum \limits_{j=1}^{n_{it}}{\delta}_{i,j}, $$
with
![]() $ {n}_{it} $
being the number of observations contained in a given cluster and
$ {n}_{it} $
being the number of observations contained in a given cluster and
![]() $ {\delta}_{i,j} $
being equal to 1, if the
$ {\delta}_{i,j} $
being equal to 1, if the
![]() $ i $
th species is contained in the reduced mechanism of the
$ i $
th species is contained in the reduced mechanism of the
![]() $ j $
th sample, or 0 otherwise. In light of its definition, the
$ j $
th sample, or 0 otherwise. In light of its definition, the
![]() $ \lambda $
coefficient can be seen as a metric to assess the cluster uniformity from a chemical point of view, being equal to 0 if the observations in a given cluster are chemically homogeneous, and equal to 1 in case of complete nonuniformity.
$ \lambda $
coefficient can be seen as a metric to assess the cluster uniformity from a chemical point of view, being equal to 0 if the observations in a given cluster are chemically homogeneous, and equal to 1 in case of complete nonuniformity.
Table 2. Reduction of the chemical mechanisms via directed graph with error propagation on the basis of the local principal component analysis thermochemical space prepartitioning with
![]() $ \mathrm{k}=7 $
: average number of species (
$ \mathrm{k}=7 $
: average number of species (
![]() $ {\mathrm{n}}_{\mathrm{sp}}^{\mathrm{mean}} $
), maximum number of species (
$ {\mathrm{n}}_{\mathrm{sp}}^{\mathrm{mean}} $
), maximum number of species (
![]() $ {\mathrm{n}}_{\mathrm{sp}}^{\mathrm{max}} $
), minimum number of species (
$ {\mathrm{n}}_{\mathrm{sp}}^{\mathrm{max}} $
), minimum number of species (
![]() $ {\mathrm{n}}_{\mathrm{sp}}^{\mathrm{min}} $
), average nonuniformity coefficient (
$ {\mathrm{n}}_{\mathrm{sp}}^{\mathrm{min}} $
), average nonuniformity coefficient (
![]() $ {\unicode{x03BB}}_{\mathrm{mean}} $
), and maximum nonuniformity coefficient (
$ {\unicode{x03BB}}_{\mathrm{mean}} $
), and maximum nonuniformity coefficient (
![]() $ {\unicode{x03BB}}_{\mathrm{max}} $
).
$ {\unicode{x03BB}}_{\mathrm{max}} $
).

4.2. Multidimensional adaptive simulations
4.2.1. A posteriori comparison of the classifiers
The new classifier combining the FE step and ANN (hereinafter referred to as FENN) was tested on the four laminar heptane flames described in Section 3, with BCs reported in Table 1. Its performances were firstly compared for the flame S1, in terms of accuracy and speed-up with respect to the detailed simulation, with the standard PCA-based classifier used in D’Alessio et al. (Reference D’Alessio, Parente, Stagni and Cuoci2020c), as well as with an s-ANN classifier, both operating on the full thermochemical space. Afterwards, the performances of the classifier for numerical simulations differing from the training one were assessed for flames S2, U1, and U2 reported in Table 1.
A Normalized Root-Mean-Square Error (NRMSE) between the detailed and adaptive simulations for temperature and selected species was adopted as a measure of the accuracy of the proposed methodology. The NRMSE is defined as
 $$ NRMSE=\frac{1}{\overline{y}}\cdot \sqrt{\frac{\sum_{i=1}^N{\left({\hat{y}}_i-{y}_i\right)}^2}{N}}, $$
$$ NRMSE=\frac{1}{\overline{y}}\cdot \sqrt{\frac{\sum_{i=1}^N{\left({\hat{y}}_i-{y}_i\right)}^2}{N}}, $$
with
![]() $ {\hat{y}}_i $
and
$ {\hat{y}}_i $
and
![]() $ {y}_i $
being the values obtained by means of the detailed and adaptive simulations, respectively, and
$ {y}_i $
being the values obtained by means of the detailed and adaptive simulations, respectively, and
![]() $ \overline{y} $
the mean value of the measured variable throughout the field.
$ \overline{y} $
the mean value of the measured variable throughout the field.
The network architectures consisted of two HLs for both FENN and s-ANN. The size, as well as the values for the other hyperparameters, was set after a thorough optimization and sensitivity analysis to achieve a satisfactory accuracy in the offline class prediction. The optimal network training parameters are reported in Table 3.
Table 3. Training options for the s-ANN and FENN on-the-fly classifiers: number of layers and number of neurons per layer (HLs’ size), selected activation function for the hidden layers (HLs’ activation), selected activation function for the output layer (output activation), and number of observations chosen for the training batches (batch size).

Abbreviation: ReLU, rectified linear unit.
As outlined in Table 3, the activation functions chosen for the HLs were in both cases ReLU (rectified linear unit), with a Softmax activation for the output layer, as required in case of multiclass classification tasks. By means of the Softmax function, reported in Equation (13), a class membership score
![]() $ {\boldsymbol{\sigma}}_i\in \left[0,1\right] $
(with
$ {\boldsymbol{\sigma}}_i\in \left[0,1\right] $
(with
![]() $ i\in \left[1,k\right] $
) is attributed to each observation, with their sum being equal to 1. Thus, it can be seen as a probability distribution over the different classes, and the final label is assigned to the class for which the probability is maximized.
$ i\in \left[1,k\right] $
) is attributed to each observation, with their sum being equal to 1. Thus, it can be seen as a probability distribution over the different classes, and the final label is assigned to the class for which the probability is maximized.
 $$ {\boldsymbol{\sigma}}_i\left(\mathbf{z}\right)=\frac{e^{z_i}}{\sum_{j=1}^k{e}^{z_j}}. $$
$$ {\boldsymbol{\sigma}}_i\left(\mathbf{z}\right)=\frac{e^{z_i}}{\sum_{j=1}^k{e}^{z_j}}. $$
Moreover, two different strategies were adopted to avoid the network overfitting: the initial dataset was firstly split into two different sets, one for training (
![]() $ {\mathbf{X}}_{train} $
, 70% of the original training data) and one for testing (
$ {\mathbf{X}}_{train} $
, 70% of the original training data) and one for testing (
![]() $ {\mathbf{X}}_{test} $
, remaining 30% of the original training data), and early stopping was adopted. Consequently, instead of the prescribed 200 epochs, only a fraction was necessary before the training automatically stopped (29 epochs for s-ANN net, and 38 for the FENN net), as the classification accuracy for the validation set had reached a plateau.
$ {\mathbf{X}}_{test} $
, remaining 30% of the original training data), and early stopping was adopted. Consequently, instead of the prescribed 200 epochs, only a fraction was necessary before the training automatically stopped (29 epochs for s-ANN net, and 38 for the FENN net), as the classification accuracy for the validation set had reached a plateau.
With regard to the FE step, as mentioned in Section 2.2, a linear projection method such as PCA was considered to be preferable for both the training and the on-the-fly steps with respect to other complex, nonlinear, methods. The choice of the reduced manifold dimensionality, that is, the number of training PCs to retain, was taken evaluating the original data variance,
![]() $ t $
, explained by the new set of coordinates. The latter can be easily computed in the preprocessing step as the ratio between the cumulative sum up to the qth retained eigenvalues, and the sum of the full set of eigenvalues:
$ t $
, explained by the new set of coordinates. The latter can be easily computed in the preprocessing step as the ratio between the cumulative sum up to the qth retained eigenvalues, and the sum of the full set of eigenvalues:
 $$ t=\frac{\sum_{i=1}^q{\lambda}_i}{\sum_{\hskip0.5pt j=1}^q{\lambda}_j}. $$
$$ t=\frac{\sum_{i=1}^q{\lambda}_i}{\sum_{\hskip0.5pt j=1}^q{\lambda}_j}. $$
The explained variance curve obtained evaluating
![]() $ t $
with the eigenvalues of the training dataset is reported in Figure 2: in light of this, the number of PCs to retain was set equal to
$ t $
with the eigenvalues of the training dataset is reported in Figure 2: in light of this, the number of PCs to retain was set equal to
![]() $ 70 $
, as this value was enough to recover
$ 70 $
, as this value was enough to recover
![]() $ 99.\overline{9} $
% of the original data variance, without losing any percentage, albeit small, of information after the projection on the low-dimensional manifold. Additional information regarding the a priori choice and the a posteriori assessment of the reduced dimensionality can be found in Section 4.2.2.
$ 99.\overline{9} $
% of the original data variance, without losing any percentage, albeit small, of information after the projection on the low-dimensional manifold. Additional information regarding the a priori choice and the a posteriori assessment of the reduced dimensionality can be found in Section 4.2.2.

Figure 2. Evolution of the explained original data variance with respect to the number of retained PCs.
The errors obtained from the three adaptive simulations of the S1 flame (using the LPCA, s-ANN, and FENN classifiers, respectively) are firstly compared by means of a boxplot. The latter is a statistical tool to analyze distributions: the lower and upper edges of the box represent the interquartile range, that is, the distribution going from the 25th percentile (Q1), to the 75th percentile (Q3), whereas the red line represents its median. The upper and lower lines outside the box, instead, connect Q1 and Q3 with the minimum and the maximum of the distribution, which can be obtained subtracting and adding the quantity
![]() $ 1.5 \ast IQR $
to Q1 and Q3, respectively. Any point identified as an outlier, with respect to the considered distribution, is identified by a single point outside the box. In Figure 3, three boxplots representing the NRMSEs distribution considering temperature, main reactants, and radicals (i.e.,
$ 1.5 \ast IQR $
to Q1 and Q3, respectively. Any point identified as an outlier, with respect to the considered distribution, is identified by a single point outside the box. In Figure 3, three boxplots representing the NRMSEs distribution considering temperature, main reactants, and radicals (i.e.,
![]() $ T $
, O
$ T $
, O
![]() $ {}_2 $
, H
$ {}_2 $
, H
![]() $ {}_2 $
O, CO, CO
$ {}_2 $
O, CO, CO
![]() $ {}_2 $
, CH
$ {}_2 $
, CH
![]() $ {}_3 $
, O, OH, HO
$ {}_3 $
, O, OH, HO
![]() $ {}_2 $
,
$ {}_2 $
,
![]() $ {\mathrm{C}}_2{\mathrm{H}}_2 $
, CH
$ {\mathrm{C}}_2{\mathrm{H}}_2 $
, CH
![]() $ {}_4 $
, and n-C
$ {}_4 $
, and n-C
![]() $ {}_7 $
H
$ {}_7 $
H
![]() $ {}_{16} $
) are reported for the adaptive simulations of the S1 laminar flame using the LPCA, s-ANN, and FENN classifiers, respectively.
$ {}_{16} $
) are reported for the adaptive simulations of the S1 laminar flame using the LPCA, s-ANN, and FENN classifiers, respectively.

Figure 3. Boxplot representing the normalized root-mean-square error distribution for the three adaptive simulations using local principal component analysis, s-ANN, and FENN, respectively. The error distributions were computed considering the profiles of main reactants and radicals:
![]() $ T $
, O
$ T $
, O
![]() $ {}_2 $
, H
$ {}_2 $
, H
![]() $ {}_2 $
O, CO, CO
$ {}_2 $
O, CO, CO
![]() $ {}_2 $
, CH
$ {}_2 $
, CH
![]() $ {}_3 $
, O, OH, HO
$ {}_3 $
, O, OH, HO
![]() $ {}_2 $
, C
$ {}_2 $
, C
![]() $ {}_2 $
H
$ {}_2 $
H
![]() $ {}_2 $
,
$ {}_2 $
,
![]() $ {CH}_4 $
, and n-C
$ {CH}_4 $
, and n-C
![]() $ {}_7 $
H
$ {}_7 $
H
![]() $ {}_{16} $
with respect to the detailed simulation.
$ {}_{16} $
with respect to the detailed simulation.
From the boxplots in Figure 3, it is possible to observe that the three error distributions are comparable: the median values are close, as well as the two higher percentiles and the maximum values. Moreover, it is possible to appreciate the high fidelity of all the adaptive simulations with respect to the detailed one, as the errors are well below 3%.
However, an evaluation of the SPARC adaptive-chemistry approach carried out only considering the errors arising from the main reactions and radicals would be limiting in light of its final purposes and complexity. In fact, for an accurate prediction of the temperature, main species and radicals characterized by a fast chemistry (such as OH, H, and HO
![]() $ {}_2 $
), a simple skeletal mechanism would have been enough. The final purpose of the adaptive-chemistry approaches is, on the other hand, an effective reduction of the computational cost through locally optimized kinetic mechanisms, keeping a high accuracy for the heavier species, such as the pollutants, included in the detailed kinetic mechanisms. Thus, a more effective metric for the evaluation of the proposed classifiers and, consequently, of the associated adaptive-chemistry simulations, is given by the evaluation of the accuracy in the description of specific classes of species, for instance, PAHs and soot-precursor chemistry. Indeed, the formation and the consumption of species with high molecular weight, characterized by slow chemistry, cannot be accurately described by a model based on the chemical equilibrium assumption, as well as by skeletal and global mechanisms. Therefore, heavy aromatic species such as the pyrene (C
$ {}_2 $
), a simple skeletal mechanism would have been enough. The final purpose of the adaptive-chemistry approaches is, on the other hand, an effective reduction of the computational cost through locally optimized kinetic mechanisms, keeping a high accuracy for the heavier species, such as the pollutants, included in the detailed kinetic mechanisms. Thus, a more effective metric for the evaluation of the proposed classifiers and, consequently, of the associated adaptive-chemistry simulations, is given by the evaluation of the accuracy in the description of specific classes of species, for instance, PAHs and soot-precursor chemistry. Indeed, the formation and the consumption of species with high molecular weight, characterized by slow chemistry, cannot be accurately described by a model based on the chemical equilibrium assumption, as well as by skeletal and global mechanisms. Therefore, heavy aromatic species such as the pyrene (C
![]() $ {}_{16} $
H
$ {}_{16} $
H
![]() $ {}_{10} $
) as well as two complex aromatic structures, i.e., bin1A and bin1B, which are soot precursors and the heaviest species, which are included in the examined kinetic mechanism, are considered as targets for the model evaluation. If the errors associated with the description of these species for the three numerical simulations of the S1 flame are compared, as in Figures 4–6, as well as in Table 4, the lowest one is associated with the adaptive simulation using the FENN on-the-fly classifier, and the error reduction with respect to the other two classifiers amounts up to ~50%, in case of pyrene and bin1B.
$ {}_{10} $
) as well as two complex aromatic structures, i.e., bin1A and bin1B, which are soot precursors and the heaviest species, which are included in the examined kinetic mechanism, are considered as targets for the model evaluation. If the errors associated with the description of these species for the three numerical simulations of the S1 flame are compared, as in Figures 4–6, as well as in Table 4, the lowest one is associated with the adaptive simulation using the FENN on-the-fly classifier, and the error reduction with respect to the other two classifiers amounts up to ~50%, in case of pyrene and bin1B.

Figure 4. Parity plots for the comparison of the pyrene massive concentration obtained by means of a detailed chemistry and the adaptive simulations using (a) the local principal component analysis classifier, (b) the s-ANN classifier, and (c) the FENN classifier for the S1 flame configuration, using reduced mechanisms with
![]() $ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
.
$ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
.

Figure 5. Parity plots for the comparison of the bin1A massive concentration obtained by means of a detailed chemistry and the adaptive simulations using (a) the local principal component analysis classifier, (b) the s-ANN classifier, and (c) the FENN classifier for the S1 flame configuration, using reduced mechanisms with
![]() $ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
.
$ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
.

Figure 6. Parity plots for the comparison of the bin1B massive concentration obtained by means of a detailed chemistry and the adaptive simulations using (a) the local principal component analysis classifier, (b) the s-ANN classifier, and (c) the FENN classifier for the S1 flame configuration, using reduced mechanisms with
![]() $ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
.
$ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
.
Table 4. Normalized Root Mean Square Errors (NRMSE) obtained by means of the LPCA, s-ANN, and FENN classifiers for the adaptive simulation of the S1 flame configuration with regard to the pyrene, bin1A, and bin1A mass concentrations with respect with detailed profiles.

A further confirmation of the higher efficiency and classification accuracy guaranteed by the FENN on-the-fly classifier can be found comparing the speed-up factors for the chemistry substep (S
![]() $ {}_{chem} $
) relative to the three adaptive simulations of flame S1. In Table 5, the details about the CPU time required for the chemical substep integration of the four simulations (i.e., detailed, adaptive with the LPCA classifier, adaptive with the s-ANN classifier, and adaptive with the FENN classifier) are reported by means of the average CPU time per cell (
$ {}_{chem} $
) relative to the three adaptive simulations of flame S1. In Table 5, the details about the CPU time required for the chemical substep integration of the four simulations (i.e., detailed, adaptive with the LPCA classifier, adaptive with the s-ANN classifier, and adaptive with the FENN classifier) are reported by means of the average CPU time per cell (
![]() $ {\overline{\tau}}_{chem} $
), the maximum CPU time per cell (
$ {\overline{\tau}}_{chem} $
), the maximum CPU time per cell (
![]() $ {\tau}_{chem}^{max} $
), and the relative average speed-up with respect to the detailed simulation (S
$ {\tau}_{chem}^{max} $
), and the relative average speed-up with respect to the detailed simulation (S
![]() $ {}_{chem} $
).
$ {}_{chem} $
).
Table 5. Performances of the adaptive-chemistry simulations: comparison of the CPU time (in milliseconds) required for the chemical step integration for the detailed numerical simulation and for the three adaptive simulations of the n-heptane steady laminar flame, using reduced mechanisms obtained with
![]() $ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
, and the local principal component analysis, s-ANN, and FENN classifiers, respectively, analyzing the average CPU time per cell (
$ {\unicode{x03B5}}_{\mathrm{DRGEP}}=0.005 $
, and the local principal component analysis, s-ANN, and FENN classifiers, respectively, analyzing the average CPU time per cell (
![]() $ {\overline{\unicode{x03C4}}}_{\mathrm{chem}} $
, in milliseconds), the maximum CPU time per cell (
$ {\overline{\unicode{x03C4}}}_{\mathrm{chem}} $
, in milliseconds), the maximum CPU time per cell (
![]() $ {\unicode{x03C4}}_{\mathrm{chem}}^{\mathrm{max}} $
, in milliseconds), and the relative average speed-up factor with respect to the detailed simulation (
$ {\unicode{x03C4}}_{\mathrm{chem}}^{\mathrm{max}} $
, in milliseconds), and the relative average speed-up factor with respect to the detailed simulation (
![]() $ {\mathrm{S}}_{\mathrm{chem}} $
).
$ {\mathrm{S}}_{\mathrm{chem}} $
).

Examining the values reported in Table 5, it is possible to observe that both the LPCA and s-ANN adaptive simulations are characterized by comparable mean and maximum CPU time required for the chemical step integration, while the time required for the chemistry step resolution by the FENN adaptive simulation is lower. Consequently, the adaptive simulation using FENN is characterized by a higher speed-up factor S
![]() $ {}_{chem} $
with respect to the remaining two. This can be related to the fact that both LPCA and s-ANN classifiers are assigning complex mechanisms also to cells which could require a lower number of species, such as the ones outside the reacting layer of the flame, while with the FENN, this misclassification behavior is limited.
$ {}_{chem} $
with respect to the remaining two. This can be related to the fact that both LPCA and s-ANN classifiers are assigning complex mechanisms also to cells which could require a lower number of species, such as the ones outside the reacting layer of the flame, while with the FENN, this misclassification behavior is limited.
By adopting a FENN classifier with a PCA encoding step, in addition to the advantages linked to the higher accuracy and speed-up of the adaptive simulation, it is also possible to retrieve an additional information regarding the main physicochemical processes that are occurring within the system. In fact, since it is possible to evaluate the relative importance of each PC by means of the magnitude of the associated eigenvalue, it is consequently possible to examine the most impacting chemical species, inspecting their correlation with the first PCs. In this regard, Pearson’s correlation coefficients between the chemical species and the first PCs were computed for the S1 flame, and it emerged that, in many cases, the correlation factor between a species and a PC exceeded 90%. This is the case, for instance, of C
![]() $ {}_2 $
H
$ {}_2 $
H
![]() $ {}_4 $
, C
$ {}_4 $
, C
![]() $ {}_2 $
H
$ {}_2 $
H
![]() $ {}_6 $
, and CH
$ {}_6 $
, and CH
![]() $ {}_3 $
COCH
$ {}_3 $
COCH
![]() $ {}_3 $
with the first PC (a correlation coefficient equal to 95, 91, and 92% was found, respectively) or C
$ {}_3 $
with the first PC (a correlation coefficient equal to 95, 91, and 92% was found, respectively) or C
![]() $ {}_{12} $
H
$ {}_{12} $
H
![]() $ {}_8 $
and C
$ {}_8 $
and C
![]() $ {}_{14} $
H
$ {}_{14} $
H
![]() $ {}_8 $
with the second PCs (a correlation coefficient equal to 90 and 88% was found, respectively). The strong relation between the aforementioned species and the PCs is graphically shown in Figure 7, where the concentrations (by mass) of the highest correlated species and the associated PC are shown on the left and the right of each contour, respectively.
$ {}_8 $
with the second PCs (a correlation coefficient equal to 90 and 88% was found, respectively). The strong relation between the aforementioned species and the PCs is graphically shown in Figure 7, where the concentrations (by mass) of the highest correlated species and the associated PC are shown on the left and the right of each contour, respectively.

Figure 7. Maps of massive fractions for the species with the highest correlation factor with one of the first PCs (left side of each contour), and map of the score they are most correlated with (right side of each contour): (a) C
![]() $ {}_2 $
H
$ {}_2 $
H
![]() $ {}_4 $
and first score; (b) CH
$ {}_4 $
and first score; (b) CH
![]() $ {}_3 $
COCH
$ {}_3 $
COCH
![]() $ {}_3 $
and first score; (c) C
$ {}_3 $
and first score; (c) C
![]() $ {}_{12} $
H
$ {}_{12} $
H
![]() $ {}_8 $
and second score; (d) C
$ {}_8 $
and second score; (d) C
![]() $ {}_{14} $
H
$ {}_{14} $
H
![]() $ {}_{10} $
and second score.
$ {}_{10} $
and second score.
4.2.2. A priori and a posteriori assessment of the choice of the reduced dimensionality in the feature extraction classifier
As reported in Section 2.2, PCA was chosen to be coupled with the ANN classifier for the FE step because of the considerable advantage of requiring only few parameters for the training, without the need for a thorough sensitivity analysis like most machine learning algorithms.
The only PCA hyperparameter which can have an impact on the accuracy of the classification, and consequently on the accuracy and the speed-up of the adaptive simulation, is the dimensionality of the manifold encoding the thermochemical space. In fact, a too strong dimensionality reduction could lead to an excessive compression of the initial data, with a consequent loss of information. On the other hand, a mild dimensionality reduction could, first of all, not be beneficial to solve the input dimensionality issue and, moreover, entails the inclusion of redundant information (i.e., data noise, usually found on the last PCs) that could compromise the accuracy of the classifier. Unlike other FE techniques (both linear and nonlinear) mentioned in Section 2.2, PCA is able to indicate a priori which is the optimal dimensionality of the manifold. In fact, by using Equation (14), it is possible to retrieve the amount of original data variance being explained by the selected set of PCs, computing the ratio between the cumulative sum of the eigenvalues and their total sum. Nevertheless, as pointed out by the authors in D’Alessio et al. (Reference D’Alessio, Attili, Cuoci, Pitsch and Parente2020a), the choice of the dimensionality by means of the explained variance criterion should always be supported by the examination of the profiles for the reconstructed training variables, as the explained variance can also be influenced by other factors, such as the scaling technique. In general, it can be considered as a sufficient reduced basis the one which can ensure, in addition to an almost unitary explained original data variance, a reconstruction error (in terms of NRMSE) for the variables of the training dataset below 5%.
As outlined in Section 4.2.1, a reduced basis consisting of 70 PCs was adopted for the FENN simulations, as the latter ensures that only 0.1% of the original data variance is lost, while achieving a dimensionality reduction greater than 50%. Moreover, with the considered dimensionality, the observed NRMSEs for temperature and chemical species were all below 5%, as shown in Figure 8.

Figure 8. Parity plot for the original and reconstructed profile via principal component analysis, retaining 70 PCs, for (a) temperature, (b) carbon monoxide, (c) n-heptane, (d) pyrene, (e) bin1B, and (f) bin1A.
To prove the validity of the a priori method to assess the dimensionality of the reduced manifold, several adaptive simulations were carried out varying the number of retained PCs in the on-the-fly classification, and their results were compared a posteriori. In particular, four additional adaptive simulations with an on-the-fly classifier combining PCA and ANN were tested retaining 20, 40, 90, and 120 PCs, respectively. Figure 9 shows the boxplots for the error distributions for the aforementioned adaptive simulations, focusing on the following species: bin1A, bin1B, and pyrene.

Figure 9. Boxplot representing the normalized root-mean-square error distribution for the adaptive simulations using an on-the-fly classifier combining principal component analysis and artificial neural network, for an increasing number of retained PCs.
Examining Figure 9, a monotonically decreasing behavior of the error up to 70 modes can be observed. After hitting a minimum below 10%, the median stabilizes around 15% if a higher number of retained PCs is considered.
The very large errors observed for the adaptive simulation with 20 PCs can be explained by the relatively high compression, which entails a too large loss of information. In case 40 PCs are retained, the loss of variance is limited to 1% only. However, the NMRSEs for the variables’ profile reconstruction are higher than the 5% range, as for the combustion products and main radicals (such as H
![]() $ {}_2 $
O, OH, and O) the error can reach
$ {}_2 $
O, OH, and O) the error can reach
![]() $ \sim $
12%, as shown in Figure 10. Thus, the reduced basis with 40 PCs still cannot be considered as optimal because of the information loss between the compression and reconstruction processes.
$ \sim $
12%, as shown in Figure 10. Thus, the reduced basis with 40 PCs still cannot be considered as optimal because of the information loss between the compression and reconstruction processes.

Figure 10. Parity plot for the original and reconstructed profile via principal component analysis, retaining 40 PCs, for (a) water, (b) oxygen radical, and (c) hydroxyl radical.
For the adaptive simulations with an encoding step accounting for 90 and 120 modes, the errors are slightly higher than the ones observed with 70 PCs, despite the subsets ensure a unitary variance and NRMSE well below 5%. This is due to the fact that the ANN input space has to account for a larger number of variables, as well as because the reduced basis is including redundant information on the last PCs, thus making the classification process more complex.
4.2.3. Adaptive simulations with FENN classification on test simulations
As already mentioned in Section 3, after the validation and the a posteriori comparison of the adaptive simulations for the S1 flame carried out by means of the FENN classifier, three additional adaptive simulations for the S2, U1, and U2 flame configurations were carried out. The motivation was to ascertain the capability of the combined FE and ANN classification model to adapt to different cases in terms of physical and chemical features, to guarantee that a trained model can be used for different configurations. For the test cases, the performances of the FENN classifier were also evaluated focusing on the heavier species, i.e., PAHs and soot precursors. In Figure 11, the parity plots for the profiles of the species bin1A and bin1B are reported. Figure 12a–c shows a comparison of the contours obtained by means of the detailed and adaptive simulations using FENN for the following species: AC
![]() $ {}_3 $
H
$ {}_3 $
H
![]() $ {}_4 $
, C
$ {}_4 $
, C
![]() $ {}_{14} $
H
$ {}_{14} $
H
![]() $ {}_9 $
, and C
$ {}_9 $
, and C
![]() $ {}_{16} $
H
$ {}_{16} $
H
![]() $ {}_{10} $
, respectively. From this figure, it is possible to appreciate the accuracy of the adaptive simulation, despite the Reynolds number of the numerical simulation was changed with respect to the one used for the training. In particular, examining the NRMSE reported in Figure 11a,b for bin1A and bin1B, respectively, it is possible to notice that it is exactly of the same order of magnitude (about 20 and 5%, respectively) of the one observed for the S1 flame FENN adaptive simulation. Moreover, for the other considered PAHs and soot precursors (up to C
$ {}_{10} $
, respectively. From this figure, it is possible to appreciate the accuracy of the adaptive simulation, despite the Reynolds number of the numerical simulation was changed with respect to the one used for the training. In particular, examining the NRMSE reported in Figure 11a,b for bin1A and bin1B, respectively, it is possible to notice that it is exactly of the same order of magnitude (about 20 and 5%, respectively) of the one observed for the S1 flame FENN adaptive simulation. Moreover, for the other considered PAHs and soot precursors (up to C
![]() $ {}_{16} $
), the maps of mass fractions of the FENN adaptive simulation (right side of each contour reported in Figure 12) are indistinguishable from the ones obtained by means of the detailed simulation (left side of each contour reported in Figure 12).
$ {}_{16} $
), the maps of mass fractions of the FENN adaptive simulation (right side of each contour reported in Figure 12) are indistinguishable from the ones obtained by means of the detailed simulation (left side of each contour reported in Figure 12).

Figure 11. (a) Parity plot of bin1A concentration for the n-heptane steady laminar flame S2 obtained using the FENN classifier. (b) Parity plot of bin1B concentration for the n-heptane steady laminar flame S2 obtained using the FENN classifier.

Figure 12. Maps of massive fractions obtained from the detailed simulation (left) compared to the ones obtained from the adaptive simulation of the S2 flame configuration using both FENN classifier and reduced mechanisms trained on the prepartitioning detailed simulation of the S1 flame configuration (right) for (a) AC
![]() $ {}_3 $
H
$ {}_3 $
H
![]() $ {}_3 $
, (b) C
$ {}_3 $
, (b) C
![]() $ {}_{14} $
H
$ {}_{14} $
H
![]() $ {}_9 $
, and (c) C
$ {}_9 $
, and (c) C
![]() $ {}_{16} $
H
$ {}_{16} $
H
![]() $ {}_{10} $
.
$ {}_{10} $
.
The possibility of having such an accurate adaptive simulation with new BCs is due to the fact that the on-the-fly classification is not made on the thermochemical state of the flame, but on its features. In fact, as previously proved by means of the S1 flame adaptive simulations, it is possible to increase the accuracy of the classifier, if compared to a s-ANN classifier on the thermochemical space, by reducing the input space dimensionality, thus attenuating the so-called curse of dimensionality. Furthermore, the features of a flame are, in general, less dependent from one or more BCs imposed to the simulation. Therefore, the classification accuracy (and, consequently, the accuracy of the numerical simulation) is higher when compared to the one made on the thermochemical space. To prove this last statement, the simulation of the S2 flame configuration was also carried out using the previous s-ANN classifier, and the results were compared with the ones obtained by means of the FENN classifier. In Tables 6 and 7, the NRMSEs of the two adaptive simulations for the S2 flame using the two aforementioned on-the-fly classifiers are reported for the main species and PAHs, respectively. While for the DRGEP target species (n-C
![]() $ {}_7 $
H
$ {}_7 $
H
![]() $ {}_{16} $
and O
$ {}_{16} $
and O
![]() $ {}_2 $
), as well as for temperature and light radicals (O, H, and OH), the two errors are comparable and very low, as reported in Table 6, once again, the adaptive simulation with the FENN classifier proves to be more reliable for the prediction of heavy aromatic radicals and soot precursors. As shown in Table 7, the errors are lower for all the examined species, and reduced of a factor of 2 for C
$ {}_2 $
), as well as for temperature and light radicals (O, H, and OH), the two errors are comparable and very low, as reported in Table 6, once again, the adaptive simulation with the FENN classifier proves to be more reliable for the prediction of heavy aromatic radicals and soot precursors. As shown in Table 7, the errors are lower for all the examined species, and reduced of a factor of 2 for C
![]() $ {}_7 $
H
$ {}_7 $
H
![]() $ {}_8 $
, Pyrene, and bin1B. Moreover, the FENN simulation for the S2 flame is still faster than the s-ANN one, with the speed-up for the chemistry step,
$ {}_8 $
, Pyrene, and bin1B. Moreover, the FENN simulation for the S2 flame is still faster than the s-ANN one, with the speed-up for the chemistry step,
![]() $ {S}_{chem} $
, being equal to 3.44 and 3.40, respectively, on higher terms of simulation accuracy. In conclusion, the possibility to have a more accurate and, at the same time, faster simulation, on equal terms of offline training (i.e., prepartitioning method and reduced mechanisms), can be only interpreted due to a higher on-the-fly classification accuracy.
$ {S}_{chem} $
, being equal to 3.44 and 3.40, respectively, on higher terms of simulation accuracy. In conclusion, the possibility to have a more accurate and, at the same time, faster simulation, on equal terms of offline training (i.e., prepartitioning method and reduced mechanisms), can be only interpreted due to a higher on-the-fly classification accuracy.
Table 6. Normalized Root Mean Square Errors obtained by means of the s-ANN and FENN classifiers for the adaptive simulation of the S2 flame configuration with regard to the temperature, target species, and fast-chemistry radicals.

Table 7. Normalized Root Mean Square Errors obtained by means of the s-ANN and FENN classifiers for the adaptive simulation of the S2 flame configuration with regard to polycyclic aromatic hydrocarbons and soot precursors.

Finally, the two unsteady simulations U1 and U2, carried out with the FENN classifier, are evaluated examining the NRMSE (with respect to the detailed simulation) behavior in time. In Figure 13a,b, the curves relative to the error for bin1A, bin1B, and pyrene for the U1 and U2 simulations are reported, respectively. When unsteady conditions are imposed, as expected, the observed errors for these variables are, in general, slightly higher than the ones for steady conditions, that is, S1 and S2 simulations. In particular, the errors can vary depending on the considered timestep because of the variations of the chemical state due to the sinusoidal solicitation in the inlet velocity profile. The error behavior in time for both the adaptive simulations is similar: after an initial phase of amplification up to
![]() $ t=0.03 $
s, where a maximum is reached, it has a steep and fast decrease. However, since after the initial amplification phase the error is stabilized around an asymptotic value, which is
$ t=0.03 $
s, where a maximum is reached, it has a steep and fast decrease. However, since after the initial amplification phase the error is stabilized around an asymptotic value, which is
![]() $ \sim $
8% for bin1B and Pyrene and
$ \sim $
8% for bin1B and Pyrene and
![]() $ \sim $
25% for bin1A, and it does not keep amplifying in time, the application of the FENN classifier is verified also for the two unsteady simulations U1 and U2.
$ \sim $
25% for bin1A, and it does not keep amplifying in time, the application of the FENN classifier is verified also for the two unsteady simulations U1 and U2.

Figure 13. Behavior in time of the Normalized Root Mean Square Error observed for the unsteady adaptive simulations carried out with an FENN classifier and using (a)
![]() $ \mathrm{f} $
= 20 Hz and
$ \mathrm{f} $
= 20 Hz and
![]() $ \mathrm{A} $
= 0.5 as parameters for the sinusoidal perturbation of the fuel velocity inlet and (b)
$ \mathrm{A} $
= 0.5 as parameters for the sinusoidal perturbation of the fuel velocity inlet and (b)
![]() $ \mathrm{f} $
= 40 Hz and
$ \mathrm{f} $
= 40 Hz and
![]() $ \mathrm{A} $
= 0.75 as parameters for the sinusoidal perturbation of the fuel velocity inlet. Orange solid line with upward pointing triangle markers: bin1B; green solid line with diamond markers: bin1A; gray solid line with squared markers: pyrene.
$ \mathrm{A} $
= 0.75 as parameters for the sinusoidal perturbation of the fuel velocity inlet. Orange solid line with upward pointing triangle markers: bin1B; green solid line with diamond markers: bin1A; gray solid line with squared markers: pyrene.
5. Conclusions
In this work, a novel on-the-fly classifier based on the combination of FE and ANNs was proposed and tested to perform adaptive-chemistry simulations using large kinetic mechanisms, accounting for hundreds of chemical species. The preprocessing steps of the chosen adaptive-chemistry methodology (SPARC) remained unchanged (i.e., the prepartitioning of the composition space and the creation of a library of reduced mechanisms via DRGEP), but a neural architecture with a prior encoding step via PCA was integrated in the CFD numerical solver for the on-the-fly classification task. At each timestep of the CFD simulation, the thermochemical states associated with each grid point are projected on a lower-dimensional manifold spanned by the PCA eigenvectors, and then they are passed through an ANN to be classified.
In case high-dimensional spaces are considered, a high accuracy for the supervised classification step can be hard to accomplish, both if the label assignment is based on the computation of a
![]() $ {L}_k $
norm, or using ANN. In this regard, the presence of a FE step can be beneficial, as lowering the number of features entails the removal of the data noise and a modification of the hyperspace geometry, which promotes the separation between classes, thus increasing the classification accuracy.
$ {L}_k $
norm, or using ANN. In this regard, the presence of a FE step can be beneficial, as lowering the number of features entails the removal of the data noise and a modification of the hyperspace geometry, which promotes the separation between classes, thus increasing the classification accuracy.
The new classifier (FENN) was firstly successfully tested for the simulation of a steady 2D, nitrogen-diluted, n-heptane laminar coflow diffusion flame in air, and its performances were compared with a classifier based on the PCA reconstruction error, as well as with a s-ANN classifier operating on the full thermochemical space. The original detailed kinetic mechanism accounted for 172 species and 6,067 reactions, while the library of reduced mechanisms was obtained by means of the DRGEP algorithm, imposing a reduction tolerance equal to
![]() $ {\epsilon}_{DRGEP}=0.005 $
. From the comparison of the three classifiers, it was clear that carrying out the classification in the feature space, instead of the thermochemical space, enhances the model performances. In fact, although comparable results were obtained with regard to the temperature, the main species (fuel and oxidizer) and the fast radicals (such as H, O, and OH), the simulations carried out with the FENN classifier provided an increase in the accuracy of a factor of 2 with respect to the heavy, aromatic, species, such as PAHs and soot precursors. Moreover, the adaptive simulation using a FENN classifier was also characterized by a higher speed-up factor than the other two (equal to 4.03, while 3.48 and 3.49 were the speed-up factors for the adaptive simulations using the PCA classifier and the s-ANN architecture, respectively), thus entailing a smaller percentage of misclassified points.
$ {\epsilon}_{DRGEP}=0.005 $
. From the comparison of the three classifiers, it was clear that carrying out the classification in the feature space, instead of the thermochemical space, enhances the model performances. In fact, although comparable results were obtained with regard to the temperature, the main species (fuel and oxidizer) and the fast radicals (such as H, O, and OH), the simulations carried out with the FENN classifier provided an increase in the accuracy of a factor of 2 with respect to the heavy, aromatic, species, such as PAHs and soot precursors. Moreover, the adaptive simulation using a FENN classifier was also characterized by a higher speed-up factor than the other two (equal to 4.03, while 3.48 and 3.49 were the speed-up factors for the adaptive simulations using the PCA classifier and the s-ANN architecture, respectively), thus entailing a smaller percentage of misclassified points.
To extend the possibility to use the FENN classifier also to numerical setups which are different than the ones used for the training, i.e., with different BCs, three additional adaptive simulations were carried out: one in steady condition, but with a higher Reynolds number, and other two in unsteady conditions. The latter were obtained imposing a time-dependent sinusoidal perturbation to the fuel parabolic velocity profile. The accuracy in the PAHs and soot-precursors chemistry description observed for the adaptive simulation for the flame configuration with higher Reynolds was of the same order of magnitude of the previous one, as well as the speed-up. Moreover, the FENN classifier, compared to an ANN architecture classifying the thermochemical space, lead to a factor of 2 accuracy increase, while keeping a higher speed-up factor with respect to the detailed simulation. Finally, for the two unsteady adaptive test simulations, the error did not amplify, but instead steeply decreased and asymptotized toward the values observed for the steady simulations.
Funding Statement
The first author has received funding from the Fonds National de la Recherche Scientifique (FRS-FNRS) through an FRIA fellowship. This research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program under grant agreement No 714605.
Competing Interests
The authors declare no competing interests exist.
Data Availability Statement
The LPCA prepartitioning, as well as the choice of the optimal number of clusters by means of the DB index, was accomplished using the OpenMORe framework, an open-source Python tool for clustering, model order reduction, and data analysis. It is available at the following address: https://github.com/burn-research/OpenMORe.
The numerical simulations were carried out with the laminarSMOKE code, a CFD solver based on OpenFOAM and specifically conceived for laminar reacting flows with detailed kinetic mechanisms. It is available at the following address: https://github.com/acuoci/laminarSMOKE.
Author Contributions
Conceptualization, G.D.A., A.C., A.P.; Methodology, G.D.A., A.C., A.P.; Data curation, G.D.A.; Software, G.D.A., A.C.; Writing original draft, G.D.A.; Writing review and editing, G.D.A., A.C., A.P.; Project administration, A.P.; Supervision, A.C., A.P.; All authors approved the final submitted draft.

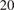



































































Comments
No Comments have been published for this article.