Article contents
COINTEGRATION IN FUNCTIONAL AUTOREGRESSIVE PROCESSES
Published online by Cambridge University Press: 22 November 2019
Abstract
This article defines the class of 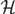 ${\cal H}$-valued autoregressive (AR) processes with a unit root of finite type, where
${\cal H}$-valued autoregressive (AR) processes with a unit root of finite type, where 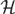 ${\cal H}$ is a possibly infinite-dimensional separable Hilbert space, and derives a generalization of the Granger–Johansen Representation Theorem valid for any integration order
${\cal H}$ is a possibly infinite-dimensional separable Hilbert space, and derives a generalization of the Granger–Johansen Representation Theorem valid for any integration order 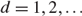 $d = 1,2, \ldots$. An existence theorem shows that the solution of an AR process with a unit root of finite type is necessarily integrated of some finite integer order d, displays a common trends representation with a finite number of common stochastic trends, and it possesses an infinite-dimensional cointegrating space when
$d = 1,2, \ldots$. An existence theorem shows that the solution of an AR process with a unit root of finite type is necessarily integrated of some finite integer order d, displays a common trends representation with a finite number of common stochastic trends, and it possesses an infinite-dimensional cointegrating space when 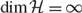 ${\rm{dim}}{\cal H} = \infty$. A characterization theorem clarifies the connections between the structure of the AR operators and (i) the order of integration, (ii) the structure of the attractor space and the cointegrating space, (iii) the expression of the cointegrating relations, and (iv) the triangular representation of the process. Except for the fact that the dimension of the cointegrating space is infinite when
${\rm{dim}}{\cal H} = \infty$. A characterization theorem clarifies the connections between the structure of the AR operators and (i) the order of integration, (ii) the structure of the attractor space and the cointegrating space, (iii) the expression of the cointegrating relations, and (iv) the triangular representation of the process. Except for the fact that the dimension of the cointegrating space is infinite when 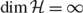 ${\rm{dim}}{\cal H} = \infty$, the representation of AR processes with a unit root of finite type coincides with the one of finite-dimensional VARs, which can be obtained setting
${\rm{dim}}{\cal H} = \infty$, the representation of AR processes with a unit root of finite type coincides with the one of finite-dimensional VARs, which can be obtained setting  ${\cal H} = ^p $ in the present results.
${\cal H} = ^p $ in the present results.
Information
- Type
- ARTICLES
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
The article benefited from useful comments from the Editor, Peter C.B. Phillips, three anonymous referees and conference and seminar participants at 2018 NBER-NSF Time Series Conference, University of California San Diego, University of Bologna and ICEEE 2019, University of Lecce. The idea of the present article was conceived while the first author was visiting the Department of Economics, Indiana University, in January 2017; the hospitality of Yoosoon Chang and Joon Park is gratefully acknowledged. During the revision of the article in September 2018, the first author visited the Department of Economics, University of California San Diego, and the hospitality of Brendan K. Beare is gratefully acknowledged. The first author acknowledges partial financial support from MIUR PRIN grant 2010J3LZEN. The views expressed in this article do not necessarily reflect those of the authors’ institutions.
References
REFERENCES
- 14
- Cited by

