Hostname: page-component-5db58dd55d-lqwgf Total loading time: 0 Render date: 2026-06-05T21:39:56.858Z Has data issue: false hasContentIssue false
  • English
  • Français

HOW TO AVOID THE ZERO-POWER TRAP IN TESTING FOR CORRELATION

Published online by Cambridge University Press:  01 March 2021

David Preinerstorfer
David Preinerstorfer*
Affiliation:
Université libre de Bruxelles
*
Address correspondence to David Preinerstorfer, European Center for Advanced Research in Economics and Statistics and Solvay Brussels School of Economics and Management, Université libre de Bruxelles, Avenue Franklin Roosevelt 50, 1050 Bruxelles, Belgium; e-mail: david.preinerstorfer@ulb.be.
Get access Rights & Permissions [Opens in a new window]

Abstract

In testing for correlation of the errors in regression models, the power of tests can be very low for strongly correlated errors. This counterintuitive phenomenon has become known as the “zero-power trap.” Despite a considerable amount of literature devoted to this problem, mainly focusing on its detection, a convincing solution has not yet been found. In this article, we first discuss theoretical results concerning the occurrence of the zero-power trap phenomenon. Then, we suggest and compare three ways to avoid it. Given an initial test that suffers from the zero-power trap, the method we recommend for practice leads to a modified test whose power converges to 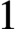$1$ as the correlation gets very strong. Furthermore, the modified test has approximately the same power function as the initial test and thus approximately preserves all of its optimality properties. We also provide some numerical illustrations in the context of testing for network generated correlation.

Information

Type
ARTICLES
Information
Econometric Theory , Volume 39 , Issue 6: SPECIAL ISSUE IN HONOR OF BENEDIKT M PÖTSCHER , December 2023 , pp. 1292 - 1324
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

I thank the Editor, Co-Editor, and two referees for helpful comments. Financial support by the Program of Concerted Research Actions (ARCs) of the Université libre de Bruxelles is gratefully acknowledged.

References

REFERENCES

Davies, R.B. (1980) Algorithm AS 155: The distribution of a linear combination of ${\chi}^2$ random variables. Journal of the Royal Statistical Society. Series C (Applied Statistics) 29(3), 323–333.Google Scholar
Fan, J., Liao, Y., & Yao, J. (2015) Power enhancement in high-dimensional cross-sectional tests. Econometrica 83(4), 1497–1541.CrossRefGoogle ScholarPubMed
Horn, R.A. & Johnson, C.R. (1985) Matrix Analysis. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Kelly, M. (2019) The standard errors of persistence. CEPR Discussion paper no. DP13783.CrossRefGoogle Scholar
King, M.L. & Hillier, G.H. (1985) Locally best invariant tests of the error covariance matrix of the linear regression model. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 47, 98–102.Google Scholar
Kleiber, C. & Krämer, W. (2005) Finite-sample power of the Durbin–Watson test against fractionally integrated disturbances. Econometrics Journal 8(3), 406–417.CrossRefGoogle Scholar
Kock, A.B. & Preinerstorfer, D. (2019) Power in high-dimensional testing problems. Econometrica 87(3), 1055–1069.CrossRefGoogle Scholar
Krämer, W. (1985) The power of the Durbin–Watson test for regressions without an intercept. Journal of Econometrics 28(3), 363–370.CrossRefGoogle Scholar
Krämer, W. (2005) Finite sample power of Cliff–Ord-type tests for spatial disturbance correlation in linear regression. Journal of Statistical Planning and Inference 128(2), 489–496.CrossRefGoogle Scholar
Krämer, W. & Zeisel, H. (1990) Finite sample power of linear regression autocorrelation tests. Journal of Econometrics 43(3), 363–372.CrossRefGoogle Scholar
Leeb, H. & Pötscher, B.M. (2017) Testing in the presence of nuisance parameters: Some comments on tests post-model-selection and random critical values. In Ahmed, S.E. (ed.), Big and Complex Data Analysis: Methodologies and Applications, pp. 69–82. Springer.CrossRefGoogle Scholar
Lehmann, E.L. & Romano, J.P. (2005) Testing Statistical Hypotheses, 3rd Edition. Springer.Google Scholar
Löbus, J.-U. & Ritter, L. (2000) The limiting power of the Durbin–Watson test. Communications in Statistics: Theory and Methods 29(12), 2665–2676.CrossRefGoogle Scholar
Martellosio, F. (2010) Power properties of invariant tests for spatial autocorrelation in linear regression. Econometric Theory 26(1), 152–186.CrossRefGoogle Scholar
Martellosio, F. (2012) Testing for spatial autocorrelation: The regressors that make the power disappear. Econometric Reviews 31(2), 215–240.CrossRefGoogle Scholar
Preinerstorfer, D. (2017) Finite sample properties of tests based on prewhitened nonparametric covariance estimators. Electronic Journal of Statistics 11(1), 2097–2167.CrossRefGoogle Scholar
Preinerstorfer, D. & Pötscher, B.M. (2016) On size and power of heteroskedasticity and autocorrelation robust tests. Econometric Theory 32(2), 261–358.CrossRefGoogle Scholar
Preinerstorfer, D. & Pötscher, B.M. (2017) On the power of invariant tests for hypotheses on a covariance matrix. Econometric Theory 33(1), 1–68.CrossRefGoogle Scholar
Rudin, W. (1987) Real and Complex Analysis. McGraw-Hill Education.Google Scholar
Strasser, H. (1985) Mathematical Theory of Statistics: Statistical Experiments and Asymptotic Decision Theory. Walter de Gruyter.CrossRefGoogle Scholar
Zeisel, H. (1989) On the power of the Durbin–Watson test under high autocorrelation. Communications in Statistics: Theory and Methods 18(10), 3907–3916.CrossRefGoogle Scholar