No CrossRef data available.
Article contents
A UNIFORM BOUND ON THE OPERATOR NORM OF SUB-GAUSSIAN RANDOM MATRICES AND ITS APPLICATIONS
Published online by Cambridge University Press: 04 June 2021
Abstract
For an 
$N \times T$ random matrix 
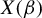$X(\beta )$ with weakly dependent uniformly sub-Gaussian entries 
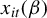$x_{it}(\beta )$ that may depend on a possibly infinite-dimensional parameter 
$\beta \in \mathbf {B}$, we obtain a uniform bound on its operator norm of the form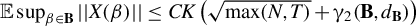 
$\mathbb {E} \sup _{\beta \in \mathbf {B}} ||X(\beta )|| \leq CK \left (\sqrt {\max (N,T)} + \gamma _2(\mathbf {B},d_{\mathbf {B}})\right )$, where C is an absolute constant, K controls the tail behavior of (the increments of) 
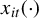$x_{it}(\cdot )$, and 
$\gamma _2(\mathbf {B},d_{\mathbf {B}})$ is Talagrand’s functional, a measure of multiscale complexity of the metric space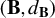 
$(\mathbf {B},d_{\mathbf {B}})$. We illustrate how this result may be used for estimation that seeks to minimize the operator norm of moment conditions as well as for estimation of the maximal number of factors with functional data.
Information
- Type
- ARTICLES
- Information
- Econometric Theory , Volume 38 , Issue 6: YALE 2018 CONFERENCE IN HONOR OF PETER C. B. PHILLIPS: PART II , December 2022 , pp. 1073 - 1091
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
We appreciate valuable comments and suggestions from Victor Chernozhukov, Guido Kuersteiner (Co-Editor), three anonymous referees, and the participants of the conference on econometrics celebrating Peter Phillips’ 40 years at Yale.
References
REFERENCES
Aue, A., Norinho, D. D., & Hörmann, S. (2015) On the prediction of stationary functional time series. Journal of the American Statistical Association 110(509), 378–392.Google Scholar
Bai, J. & Ng, S. (2002) Determining the number of factors in approximate factor models. Econometrica 70(1), 191–221.CrossRefGoogle Scholar
Bai, Z. & Silverstein, J. W. (2010) Spectral Analysis of Large Dimensional Random Matrices, Vol. 20. Springer.CrossRefGoogle Scholar
Bai, Z. D. (2008) Methodologies in spectral analysis of large dimensional random matrices, a review. In Advances In Statistics, pp. 174–240. World Scientific.CrossRefGoogle Scholar
Bandeira, A. S. & Van Handel, R. (2016) Sharp nonasymptotic bounds on the norm of random matrices with independent entries. The Annals of Probability 44(4), 2479–2506.CrossRefGoogle Scholar
Dirksen, S. (2015) Tail bounds via generic chaining. Electronic Journal of Probability 20, 1–29.CrossRefGoogle Scholar
Edelman, A. & Rao, N. R. (2005) Random matrix theory. Acta Numerica 14, 233–297.CrossRefGoogle Scholar
Fernique, X. (1976) Regularité des trajectoires des fonctions aléatoires gaussiennes. In Hennequin, P. L. (ed.), Ecole d’Eté de Probabilités de Saint-Flour IV—1974, pp. 1–96. Springer.Google Scholar
Geman, S. (1980) A limit theorem for the norm of random matrices. The Annals of Probability 8(2), 252–261.CrossRefGoogle Scholar
Guédon, O., Hinrichs, A., Litvak, A. E., & Prochno, J. (2017) On the expectation of operator norms of random matrices. In B. Klartag, E. Milman (eds.), Geometric Aspects of Functional Analysis, pp. 151–162. Springer.CrossRefGoogle Scholar
Johnstone, I. M. (2001) On the distribution of the largest eigenvalue in principal components analysis. Annals of Statistics 29(2), 295–327.CrossRefGoogle Scholar
Kargin, V. & Onatski, A. (2008) Curve forecasting by functional autoregression. Journal of Multivariate Analysis 99(10), 2508–2526.CrossRefGoogle Scholar
Khorunzhiy, O. (2012) High moments of large Wigner random matrices and asymptotic properties of the spectral norm. Random Operators and Stochastic Equations 20(1), 25–68.CrossRefGoogle Scholar
Kowal, D. R., Matteson, D. S., & Ruppert, D. (2019) Functional autoregression for sparsely sampled data. Journal of Business & Economic Statistics 37(1), 97–109.CrossRefGoogle Scholar
Latała, R. (2005) Some estimates of norms of random matrices. Proceedings of the American Mathematical Society 133(5), 1273–1282.CrossRefGoogle Scholar
Latała, R., van Handel, R., & Youssef, P. (2018) The dimension-free structure of nonhomogeneous random matrices. Inventiones Mathematicae 214(3), 1031–1080.CrossRefGoogle Scholar
Mendelson, S. & Tomczak-Jaegermann, N. (2008) A subgaussian embedding theorem. Israel Journal of Mathematics 164(1), 349–364.Google Scholar
Moon, H. R. & Weidner, M. (2017) Dynamic linear panel regression models with interactive fixed effects. Econometric Theory 33(1), 158–195.Google Scholar
Shalizi, C. & Kontorovich, A. (2010) Almost none of the theory of stochastic processes. Unpublished manuscript.Google Scholar
Talagrand, M. (2006) The Generic Chaining: Upper and Lower Bounds of Stochastic Processes. Springer Science & Business Media.Google Scholar
Tao, T. (2012) Topics in Random Matrix Theory, Vol. 132. American Mathematical Society.Google Scholar
Tao, T. & Vu, V. (2011) Random matrices: Universality of local eigenvalue statistics. Acta Mathematica 206(1), 127–204.CrossRefGoogle Scholar
Van Der Vaart, A. & Wellner, J. (1996) Weak Convergence and Empirical Processes, Vol. 58. Springer-Verlag New York.CrossRefGoogle Scholar
Vershynin, R. (2018) High-Dimensional Probability: An Introduction with Applications in Data Science, Vol. 47. Cambridge University Press.Google Scholar
Wang, J.-L., Chiou, J.-M., & Müller, H.-G. (2016) Functional data analysis. Annual Review of Statistics and Its Application 3, 257–295.CrossRefGoogle Scholar
Wigner, E. (1955) Characteristic vectors of bordered matrices with infinite dimensions. Annals of Mathematics 62(3), 548–564.CrossRefGoogle Scholar
Wishart, J. (1928) The generalised product moment distribution in samples from a normal multivariate population. Biometrika 20A, 32–52.CrossRefGoogle Scholar