Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bravo, Francesco
Chu, Ba M.
and
Jacho-Chávez, David T.
2017.
Semiparametric estimation of moment condition models with weakly dependent data.
Journal of Nonparametric Statistics,
Vol. 29,
Issue. 1,
p.
108.
Boneva, Lena Koerber
and
Linton, Oliver B.
2017.
A Discrete Choice Model for Large Heterogeneous Panels with Interactive Fixed Effects with an Application to the Determinants of Corporate Bond Issuance.
SSRN Electronic Journal ,
Boneva, Lena
and
Linton, Oliver
2017.
A discrete‐choice model for large heterogeneous panels with interactive fixed effects with an application to the determinants of corporate bond issuance.
Journal of Applied Econometrics,
Vol. 32,
Issue. 7,
p.
1226.
Muris, Chris
2017.
Estimation in the Fixed-Effects Ordered Logit Model.
The Review of Economics and Statistics,
Vol. 99,
Issue. 3,
p.
465.
Čížek, Pavel
and
Lei, Jinghua
2018.
Identification and estimation of nonseparable single-index models in panel data with correlated random effects.
Journal of Econometrics,
Vol. 203,
Issue. 1,
p.
113.
Zhu, Qianqian
Zheng, Yao
and
Li, Guodong
2018.
Linear double autoregression.
Journal of Econometrics,
Vol. 207,
Issue. 1,
p.
162.
Windmeijer, Frank
2019.
Two-stage least squares as minimum distance.
The Econometrics Journal,
Vol. 22,
Issue. 1,
p.
1.
Lee, Seojeong
and
Shin, Youngki
2021.
Complete subset averaging with many instruments.
The Econometrics Journal,
Vol. 24,
Issue. 2,
p.
290.
Escanciano, Juan Carlos
Hoderlein, Stefan
Lewbel, Arthur
Linton, Oliver
and
Srisuma, Sorawoot
2021.
NONPARAMETRIC EULER EQUATION IDENTIFICATION AND ESTIMATION.
Econometric Theory,
Vol. 37,
Issue. 5,
p.
851.
Zhang, Mengli
and
Bai, Yang
2021.
On the use of repeated measurement errors in linear regression models.
Metrika,
Vol. 84,
Issue. 5,
p.
779.
Seng, Loraine Liping
Liu, Ching‐Ti
Wang, Jingli
and
Li, Jialiang
2023.
Instrumental variable model average with applications in Mendelian randomization.
Statistics in Medicine,
Vol. 42,
Issue. 19,
p.
3547.
Harding, Matthew
Lamarche, Carlos
and
Muris, Chris
2025.
Combining Instrumental Variable Estimators for a Panel Data Model with Factors.
Journal of Business & Economic Statistics,
Vol. 43,
Issue. 3,
p.
684.
Martins, Luis F.
and
Gabriel, Vasco J.
2025.
GMM Model Averaging Using Higher Order Approximations.
Econometrics and Statistics,
Vol. 36,
Issue. ,
p.
37.
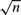 $\sqrt n$ -consistent nonlinear estimators whose cardinality increases with sample size. The method can be compared with the usual approaches of combining the moment conditions (GMM) and combining the instruments (IV), and achieves similar objectives of aggregating the available information. One advantage of aggregating the estimators rather than the moment conditions is that it yields robustness to certain types of parameter heterogeneity in the sense that it delivers consistent estimates of the mean effect in that case. We discuss the question of optimal weighting of the estimators.
$\sqrt n$ -consistent nonlinear estimators whose cardinality increases with sample size. The method can be compared with the usual approaches of combining the moment conditions (GMM) and combining the instruments (IV), and achieves similar objectives of aggregating the available information. One advantage of aggregating the estimators rather than the moment conditions is that it yields robustness to certain types of parameter heterogeneity in the sense that it delivers consistent estimates of the mean effect in that case. We discuss the question of optimal weighting of the estimators.
