Hostname: page-component-7bb8b95d7b-qxsvm Total loading time: 0 Render date: 2024-09-11T14:15:34.362Z Has data issue: false hasContentIssue false
  • English
  • Français

GAUSSIAN INFERENCE IN AR(1) TIME SERIES WITH OR WITHOUT A UNIT ROOT

Published online by Cambridge University Press:  22 January 2008

Peter C.B. Phillips  and
Chirok Han
Peter C.B. Phillips*
Affiliation:
Cowles Foundation, Yale UniversityUniversity of York and University of Auckland
Chirok Han
Affiliation:
University of Auckland
*
Address correspondence to Peter Phillips, Cowles Foundation for Research in Economics, Yale University, Box 208281, New Haven, CT 06520-8281, USA; e-mail: peter.phillips@yale.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

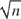This paper introduces a simple first-difference-based approach to estimation and inference for the AR(1) model. The estimates have virtually no finite-sample bias and are not sensitive to initial conditions, and the approach has the unusual advantage that a Gaussian central limit theory applies and is continuous as the autoregressive coefficient passes through unity with a uniform rate of convergence. En route, a useful central limit theorem (CLT) for sample covariances of linear processes is given, following Phillips and Solo (1992, Annals of Statistics, 20, 971–1001). The approach also has useful extensions to dynamic panels.

Type
Research Article
Information
Econometric Theory , Volume 24 , Issue 3 , June 2008 , pp. 631 - 650
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Davidson, J. (1994) Stochastic Limit Theory. Oxford University Press.CrossRefGoogle Scholar
Karanasos, M. (1998) A new method for obtaining the autocovariance of an ARMA model: An exact form solution. Econometric Theory 14, 622–640.CrossRefGoogle Scholar
Paparoditis, E. ’ Politis, D.N. (2000) Large-sample inference in the general AR(1) model. Test 9, 487–509.CrossRefGoogle Scholar
Phillips, P.C.B. ’ Magdalinos, T. (2005) Limit Theory for Moderate Deviations from a Unit Root. Cowles Foundation Discussion paper 1471, Yale University.Google Scholar
Phillips, P.C.B. ’ Solo, V. (1992) Asymptotics for linear processes. Annals of Statistics 20, 971–1001.CrossRefGoogle Scholar
White, J.S. (1958) The limiting distribution of the serial correlation coefficient in the explosive case. Annals of Mathematical Statistics 29, 1188–1197.CrossRefGoogle Scholar