Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-18T04:39:04.250Z Has data issue: false hasContentIssue false
  • English
  • Français

IDENTIFYING RESTRICTIONS FOR FINITE PARAMETER CONTINUOUS TIME MODELS WITH DISCRETE TIME DATA

Published online by Cambridge University Press:  22 December 2015

Jason R. Blevins
Jason R. Blevins*
Affiliation:
Ohio State University
*
*Address correspondence to Jason R. Blevins Ohio State University, Department of Economics, 1945 N High St., 410 Arps Hall, Columbus, OH 43210, USA; e-mail: blevins.141@osu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper revisits the question of parameter identification when a linear continuous time model is sampled only at equispaced points in time. Following the framework and assumptions of Phillips (1973), we consider models characterized by first-order, linear systems of stochastic differential equations and use a priori restrictions on the model parameters as identifying restrictions. A practical rank condition is derived to test whether any particular collection of at least 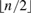$\left\lfloor {n/2} \right\rfloor$ general linear restrictions on the parameter matrix is sufficient for identification. We then consider extensions to incorporate prior restrictions on the covariance matrix of the disturbances, to identify the covariance matrix itself, and to address identification in models with cointegration.

Type
MISCELLANEA
Information
Econometric Theory , Volume 33 , Issue 3 , June 2017 , pp. 739 - 754
Copyright
Copyright © Cambridge University Press 2015 

Footnotes

I am grateful to John Geweke, Robert de Jong, Matt Masten, Tucker McElroy, Peter Phillips, and three anonymous referees for useful comments and discussions.

References

REFERENCES

Aït-Sahalia, Y. (2007) Estimating continuous-time models using discretely sampled data. In Blundell, T.P.R. and Newey, W.K. (Eds.), Advances in Economics and Econometrics: Theory and Applications, Ninth World Congress. Cambridge University Press.Google Scholar
Arcidiacono, P., Bayer, P., Blevins, J.R., & Ellickson, P.B. (2012) Estimation of dynamic discrete choice models in continuous time. Working Paper 18449, National Bureau of Economic Research.Google Scholar
Bandi, F.M. & Phillips, P.C.B. (2009) Nonstationary continuous-time processes. In Aït-Sahalia, Y. and Hansen, L.P. (Eds.), Handbook of Financial Econometrics, Volume 1, Chapter 3. Amsterdam: North Holland.Google Scholar
Baxter, M. & Rennie, A. (1996) Financial Calculus: An Introduction to Derivative Pricing. Cambridge University Press.CrossRefGoogle Scholar
Bergstrom, A.R. (1988) The history of continuous-time econometric models. Econometric Theory 4, 365–383.CrossRefGoogle Scholar
Bergstrom, A.R. & Nowman, K.B. (2007) A Continuous Time Econometric Model of the United Kingdom with Stochastic Trends. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Coddington, E.A. & Levinson, N. (1955) Theory of Ordinary Differential Equations. McGraw-Hill.Google Scholar
Culver, W.J. (1966) On the existence and uniqueness of the real logarithm of a matrix. Proceedings of the American Mathematical Society 17, 1146–1146.CrossRefGoogle Scholar
Cuthbert, J.R. (1972) On uniqueness of the logarithm for Markov semi-groups. Journal of the London Mathematical Society s2–4, 623–630.CrossRefGoogle Scholar
Cuthbert, J.R. (1973) The logarithm function for finite-state Markov semi-groups. Journal of the London Mathematical Society s2–6, 524–532.CrossRefGoogle Scholar
Doraszelski, U. & Judd, K.L. (2012) Avoiding the curse of dimensionality in dynamic stochastic games. Quantitative Economics 3, 53–93.CrossRefGoogle Scholar
Fan, J. (2005) A selective overview of nonparametric methods in financial econometrics. Statistical Science 20, 317–357.CrossRefGoogle Scholar
Gantmacher, F.R. (1959) The Theory of Matrices, Volume 1. New York: Chelsea.Google Scholar
Geweke, J. (1978) Temporal aggregation in the multiple regression model. Econometrica 46, 643–661.CrossRefGoogle Scholar
Hamerle, A., Nagl, W., & Singer, H. (1991) Problems with the estimation of stochastic differential equations using structural equations models. Journal of Mathematical Sociology 16, 201–220.CrossRefGoogle Scholar
Hansen, L.P. & Sargent, T.J. (1983) The dimensionality of the aliasing problem in models with rational spectral densities. Econometrica 51, 377–387.CrossRefGoogle Scholar
Hurwicz, L. (1950) Generalization of the concept of identification. In Koopmans, T.C. (Ed.), Statistical Inference in Dynamic Models. New York: John Wiley & Sons.Google Scholar
Kessler, M. & Rahbek, A. (2004) Identification and inference for multivariate cointegrated and ergodic Gaussian diffusions. Statistical Inference for Stochastic Processes 7, 137–151.CrossRefGoogle Scholar
Koopmans, T.C. (1949) Identification problems in economic model construction. Econometrica 17, 125–144.CrossRefGoogle Scholar
McCrorie, J.R. (2000) Deriving the exact discrete analog of a continuous time system. Econometric Theory 16, 998–1015.CrossRefGoogle Scholar
McCrorie, J.R. (2003) The problem of aliasing in identifying finite parameter continuous time stochastic models. Acta Applicandae Mathematicae 79, 9–16.CrossRefGoogle Scholar
McCrorie, J.R. (2009) Estimating continuous-time models on the basis of discrete data via an exact discrete analog. Econometric Theory 25, 1120–1137.Google Scholar
Phillips, P.C.B. (1970) The structural estimation of stochastic differential equation systems. Master’s thesis, University of Auckland.Google Scholar
Phillips, P.C.B. (1972) The structural estimation of a stochastic differential equation system. Econometrica 40, 1021–1041.CrossRefGoogle Scholar
Phillips, P.C.B. (1973) The problem of identification in finite parameter continuous time models. Journal of Econometrics 1, 351–362.CrossRefGoogle Scholar
Phillips, P.C.B. (1991) Error correction and long-run equilibrium in continuous time. Econometrica 59, 967–980.CrossRefGoogle Scholar
Phillips, P.C.B. & Yu, J. (2009) Maximum likelihood and Gaussian estimation of continuous time models in finance. In Mikosch, T., Kreiß, J.-P., Davis, R.A., and Andersen, T.G. (Eds.), Handbook of Financial Time Series, pp. 497–530. Springer.CrossRefGoogle Scholar
Schiraldi, P., Smith, H., & Takahashi, Y. (2012) Estimating a dynamic game of spatial competition: The case of the U.K. supermarket industry. Working paper, London School of Economics.Google Scholar
Sims, C.A. (1971) Discrete approximations to continuous time distributed lags in econometrics. Econometrica 39, 545–563.CrossRefGoogle Scholar
Singer, B. & Spilerman, S. (1976) The representation of social processes by Markov models. The American Journal of Sociology 82(1), 1–54.CrossRefGoogle Scholar
Sinha, N.K. & Lastman, G.J. (1982) Identification of continuous-time multivariable systems from sampled data. International Journal of Control 35, 117–126.CrossRefGoogle Scholar
Sørensen, H. (2004) Parametric inference for diffusion processes observed at discrete points in time: A survey. International Statistical Review 72, 337–354.Google Scholar
Van Loan, C.F. (1978) Computing integrals involving the matrix exponential. IEEE Transactions on Automatic Control 23, 395–404.CrossRefGoogle Scholar
Yu, J. (2014) Econometric analysis of continuous time models: A survey of Peter Phillips’ work and some new results. Econometric Theory 30, 737–774.CrossRefGoogle Scholar