Hostname: page-component-5c6d5d7d68-lvtdw Total loading time: 0 Render date: 2024-08-15T02:20:48.626Z Has data issue: false hasContentIssue false
  • English
  • Français

ROOT-N CONSISTENCY OF INTERCEPT ESTIMATORS IN A BINARY RESPONSE MODEL UNDER TAIL RESTRICTIONS

Published online by Cambridge University Press:  02 November 2017

Lili Tan  and
Yichong Zhang
Lili Tan
Affiliation:
Yunnan University
Yichong Zhang*
Affiliation:
Singapore Management University
*
*Address correspondence to Yichong Zhang, School of Economics, Singapore Management University, Singapore; e-mail: yczhang@smu.edu.sg.
Get access Rights & Permissions [Opens in a new window]

Abstract

The intercept of the binary response model is not regularly identified (i.e., 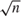$\sqrt n$ consistently estimable) when the support of both the special regressor V and the error term ε are the whole real line. The estimator of the intercept potentially has a slower than 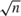$\sqrt n$ convergence rate, which can result in a large estimation error in practice. This paper imposes additional tail restrictions which guarantee the regular identification of the intercept and thus the 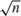$\sqrt n$-consistency of its estimator. We then propose an estimator that achieves the 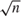$\sqrt n$ rate. Last, we extend our tail restrictions to a full-blown model with endogenous regressors.

Type
ARTICLES
Information
Econometric Theory , Volume 34 , Issue 6 , December 2018 , pp. 1180 - 1206
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We thank Shakeeb Khan, Federico Bugni, Arnaud Maurel, Xavier D’Haultfœuille, the editor, the co-editor, three anonymous referees, and the participants in the 2014 Econometric Society China Summer Meeting and the Duke microeconometrics lunch group for their comments. The first author acknowledges financial support from Project 71563062 supported by National Natural Science Foundation of China and Key Project of the National Social Science Foundation of China (Grant No. 13AZD082). The usual disclaimer applies.

References

REFERENCES

Andrews, D.W. & Schafgans, M.M. (1998) Semiparametric estimation of the intercept of a sample selection model. The Review of Economic Studies 65, 497–517.CrossRefGoogle Scholar
Blundell, R.W. & Powell, J.L. (2004) Endogeneity in semiparametric binary response models. The Review of Economic Studies 71, 655–679.Google Scholar
Chaudhuri, S. & Hill, J.B. (2015) Robust estimation for average treatment effects. Working paper, University of North Carolina, Chapel Hill.Google Scholar
Chen, S., Khan, S., & Tang, X. (2016) Informational content of special regressors in heteroskedastic binary response models. Journal of Econometrics 193, 162–182.Google Scholar
De Haan, L. & Ferreira, A. (2007) Extreme Value Theory: An Introduction, Springer Science & Business Media.Google Scholar
Dekkers, A.L. & De Haan, L. (1989) On the estimation of the extreme-value index and large quantile estimation. Annals of Statistics 17, 1795–1832.Google Scholar
D’Haultfoeuille, X., Maurel, A., & Zhang, Y. (2016) Extremal quantile regressions for selection models and the black-white wage gap. Working paper, Duke University.Google Scholar
Dong, Y. & Lewbel, A. (2015) A simple estimator for binary choice models with endogenous regressors. Econometric Reviews 34, 82–105.CrossRefGoogle Scholar
Falk, M. (1991) A note on the inverse bootstrap process for large quantiles. Stochastic Processes and Their Applications 38, 359–363.Google Scholar
Han, A.K. (1987) Non-parametric analysis of a generalized regression model: The maximum rank correlation estimator. Journal of Econometrics 35, 303–316.Google Scholar
Hill, J.B. & Renault, E. (2010) Generalized method of moments with tail trimming. Working paper, University of North Carolina, Chapel Hill.Google Scholar
Horowitz, J.L. (1992) A smoothed maximum score estimator for the binary response model. Econometrica 60, 505–531.CrossRefGoogle Scholar
Ichimura, H. (1993) Semiparametric least squares (SLS) and weighted SLS estimation of single-index models. Journal of Econometrics 58, 71–120.Google Scholar
Jacho-Chávez, D.T. (2009) Efficiency bounds for semiparametric estimation of inverse conditional-density-weighted functions. Econometric Theory 25, 847–855.Google Scholar
Khan, S. & Tamer, E. (2010) Irregular identification, support conditions, and inverse weight estimation. Econometrica 78, 2021–2042.Google Scholar
Klein, R.W. & Spady, R.H. (1993) An efficient semiparametric estimator for binary response models. Econometrica 61, 387–421.Google Scholar
Lewbel, A. (1997) Semiparametric estimation of location and other discrete choice moments. Econometric Theory 13, 32–51.CrossRefGoogle Scholar
Lewbel, A. (2000) Semiparametric qualitative response model estimation with unknown heteroscedasticity or instrumental variables. Journal of Econometrics 97, 145–177.CrossRefGoogle Scholar
Lewbel, A. & Schennach, S.M. (2007) A simple ordered data estimator for inverse density weighted expectations. Journal of Econometrics 136, 189–211.Google Scholar
Lewbel, A., McFadden, D., & Linton, O. (2011) Estimating features of a distribution from binomial data. Journal of Econometrics 162, 170–188.CrossRefGoogle Scholar
Magnac, T. & Maurin, E. (2007) Identification and information in monotone binary models. Journal of Econometrics 139, 76–104.Google Scholar
Manski, C.F. (1975) Maximum score estimation of the stochastic utility model of choice. Journal of Econometrics 3, 205–228.CrossRefGoogle Scholar
Manski, C.F. (1985) Semiparametric analysis of discrete response: Asymptotic properties of the maximum score estimator. Journal of Econometrics 27, 313–333.Google Scholar
Manski, C.F. (1988) Identification of binary response models. Journal of the American Statistical Association 83, 729–738.Google Scholar
Powell, J.L. & Stoker, T.M. (1996) Optimal bandwidth choice for density-weighted averages. Journal of Econometrics 75, 291–316.CrossRefGoogle Scholar
Powell, J.L., Stock, J.H., & Stoker, T.M. (1989) Semiparametric estimation of index coefficients. Econometrica 57, 1403–1430.CrossRefGoogle Scholar
Resnick, S.I. (1987) Extreme Values, Regular Variation, and Point Processes. Springer.CrossRefGoogle Scholar
Resnick, S.I. (2007) Heavy-tail Phenomena: Probabilistic and Statistical Modeling. Springer.Google Scholar
Robinson, P.M. (1988) Root-N-consistent semiparametric regression. Econometrica 56, 931–954.CrossRefGoogle Scholar
Stoker, T.M. (1991) Equivalence of direct, indirect and slope estimators of average derivatives. In Barnett, W., Tauchen, G., & Powell, J. (eds.), Nonparametric and Semiparametric Methods in Econometrics and Statistics, pp. 99–118. Cambridge University Press.Google Scholar
Van der Vaart, A.W. (1998) Asymptotic Statistics, vol. 3. Cambridge University Press.Google Scholar
Yang, T. (2015) Asymptotic trimming and rate adaptive inference for endogenous selection estimates. Working paper.Google Scholar
Supplementary material: File

Tan and Zhang supplementary material

Tan and Zhang supplementary material 1

Download Tan and Zhang supplementary material(File)
File 4.3 KB
Supplementary material: File

Tan and Zhang supplementary material

Tan and Zhang supplementary material 2

Download Tan and Zhang supplementary material(File)
File 2.6 KB
Supplementary material: File

Tan and Zhang supplementary material

Tan and Zhang supplementary material 3

Download Tan and Zhang supplementary material(File)
File 9 KB
Supplementary material: File

Tan and Zhang supplementary material

Tan and Zhang supplementary material 4

Download Tan and Zhang supplementary material(File)
File 53.7 KB
Supplementary material: File

Tan and Zhang supplementary material

Tan and Zhang supplementary material 5

Download Tan and Zhang supplementary material(File)
File 653 Bytes
Supplementary material: PDF

Tan and Zhang supplementary material

Tan and Zhang supplementary material 6

Download Tan and Zhang supplementary material(PDF)
PDF 423.6 KB
Supplementary material: File

Tan and Zhang supplementary material

Tan and Zhang supplementary material 7

Download Tan and Zhang supplementary material(File)
File 357.3 KB
Supplementary material: File

Tan and Zhang supplementary material

Tan and Zhang supplementary material 9

Download Tan and Zhang supplementary material(File)
File 513 Bytes