Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-14T06:20:48.324Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIFORM ASYMPTOTIC NORMALITY IN STATIONARY AND UNIT ROOT AUTOREGRESSION

Published online by Cambridge University Press:  14 April 2011

Chirok Han ,
Peter C. B. Phillips  and
Donggyu Sul
Chirok Han
Affiliation:
Korea University
Peter C. B. Phillips*
Affiliation:
Yale University, University of Auckland, University of Southampton, and Singapore Management University
Donggyu Sul
Affiliation:
University of Texas at Dallas
*
*Address correspondence to Peter C.B. Phillips, Department of Economics, Yale University Box 208281, New Haven, CT 06520-8281, USA; e-mail: peter.phillips@yale.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

While differencing transformations can eliminate nonstationarity, they typically reduce signal strength and correspondingly reduce rates of convergence in unit root autoregressions. The present paper shows that aggregating moment conditions that are formulated in differences provides an orderly mechanism for preserving information and signal strength in autoregressions with some very desirable properties. In first order autoregression, a partially aggregated estimator based on moment conditions in differences is shown to have a limiting normal distribution that holds uniformly in the autoregressive coefficient ρ, including stationary and unit root cases. The rate of convergence is 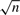when 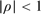and the limit distribution is the same as the Gaussian maximum likelihood estimator (MLE), but when ρ = 1 the rate of convergence to the normal distribution is within a slowly varying factor of n. A fully aggregated estimator (FAE) is shown to have the same limit behavior in the stationary case and to have nonstandard limit distributions in unit root and near integrated cases, which reduce both the bias and the variance of the MLE. This result shows that it is possible to improve on the asymptotic behavior of the MLE without using an artificial shrinkage technique or otherwise accelerating convergence at unity at the cost of performance in the neighborhood of unity. Confidence intervals constructed from the FAE using local asymptotic theory around unity also lead to improvements over the MLE.

Type
ARTICLES
Information
Econometric Theory , Volume 27 , Issue 6 , December 2011 , pp. 1117 - 1151
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abadir, K.M. (1995) Unbiased estimation as a solution to testing for random walks. Economics Letters 47, 263–268.CrossRefGoogle Scholar
Anderson, T.W. (1959) On asymptotic distributions of estimates of parameters of stochastic difference equations. Annals of Mathematical Statistics 30, 676–687.CrossRefGoogle Scholar
Andrews, D.W.K. (1988) Laws of large number for dependent non-identically distributed random variables. Econometric Theory 4, 458–467.CrossRefGoogle Scholar
Andrews, D.W.K. (1993) Exactly median-unbiased estimation of first order autoregressive/unit root models. Econometrica 61, 139–165.CrossRefGoogle Scholar
Cheang, W. & Reinsel, G.C. (2000) Bias reduction of autoregressive estimates in time series regression model through restricted maximum likelihood. Journal of the American Statistical Association 95, 1173–1184.CrossRefGoogle Scholar
Cryer, J.D., Nankervis, J.C., & Savin, N.E. (1989) Mirror-image and invariant distribution in ARMA models. Econometric Theory 5, 36–52.CrossRefGoogle Scholar
Fuller, W.A. (1976) Introduction to Statistical Time Series. Wiley.Google Scholar
Gouriéroux, C., Phillips, P.C.B., & Yu, J. (2010) Indirect inference for dynamic panel models. Journal of Econometrics 157, 68–77.CrossRefGoogle Scholar
Han, C. & Phillips, P.C.B. (2010) GMM estimation for dynamic panels with fixed effects and strong instruments at unity. Econometric Theory 26, 119–151.CrossRefGoogle Scholar
Han, C., Phillips, P.C.B., & Sul, D. (2009) X-Differencing and Dynamic Panel Model Estimation, Working paper, University of Auckland.CrossRefGoogle Scholar
Kim, Y., Qian, H., & Schmidt, P. (1999) Efficient GMM and MD estimation of autoregressive models. Economics Letters 62, 265–270.CrossRefGoogle Scholar
Lai, T.L., & Siegmund, D. (1983) Fixed accuracy estimation of an autoregressive parameter. Annals of Statistics 11, 478–485.CrossRefGoogle Scholar
McLeish, D.L. (1974) Dependent central limit theorems and invariance principles. Annals of Probability 2, 620–628.CrossRefGoogle Scholar
Park, H.J. & Fuller, W.A. (1995) Alternative estimators and unit root tests for the autoregressive process. Journal of Time Series Analysis 16, 415–429.CrossRefGoogle Scholar
Phillips, P.C.B. (1987) Towards a unified asymptotic theory for autoregression. Biometrika 74, 535–547.CrossRefGoogle Scholar
Phillips, P.C.B. (1992) Hyperconsistent Estimation of a Unit Root in Time Series Regression. Cowles Foundation Discussion Paper No. 1040.Google Scholar
Phillips, P.C.B. (1995) Fully modified least squares and vector autoregression. Econometrica 63, 1023–1078.CrossRefGoogle Scholar
Phillips, P.C.B. & Han, C. (2008) Gaussian inference in AR(1) time series with or without a unit root. Econometric Theory 24, 631–650.CrossRefGoogle Scholar
Phillips, P.C.B. & Lee, C.C., (1996) Efficiency gains from quasi-differencing under nonstationarity. In Robinson, P.M. & Rosenblatt, M. (eds.), Athens Conference on Applied Probability and Time Series: Essays in Memory of E.J. Hannan, Springer–Verlag.Google Scholar
Phillips, P.C.B., & Magdalinos, T. (2009) Unit root and cointegrating limit theory when initialization is in the infinite past. Econometric Theory 25, 1682–1715.CrossRefGoogle Scholar
Phillips, P.C.B. & Solo, V. (1992) Asymptotics for linear processes. Annals of Statistics 20, 971–1001.CrossRefGoogle Scholar
Roy, A. & Fuller, W.A. (2001) Estimation for autoregressive time series with a root near 1. Journal of Business and Economic Statistics 19, 482–493.CrossRefGoogle Scholar
Stock, J.H. (1991) Confidence intervals for the largest autoregressive root in U.S. macroeconomic time series. Journal of Monetary Economics 28, 435–459.CrossRefGoogle Scholar
White, J.S. (1958) The limiting distribution of the serial correlation coefficient in the explosive case Annals of Mathematical Statistics 29, 1188–1197.CrossRefGoogle Scholar