Literature search

The flow chart of this literature search is given in Figure 1, and the list of detailed content of studies is given in Supplementary Table S2. Based on keyword searches, 26 articles from Medline (via Ebscohost), 486 from ProQuest, 26 from PubMed, six from ScienceDirect, 44 from Scopus and 42 from Web of Science were obtained. Five additional records were identified through manual searches. From the 635 citations initially identified, 489 potential relevant articles remained after removal of duplicates (146 duplicate articles). Screening of titles and abstracts removed an additional 437 papers. A further 21 of the 52 remaining articles were excluded for not meeting the inclusion criteria after reviewing the full article. As a result, 31 articles were finally included in the review.

Fig. 1. Flow chart of literature search.

Dengue data

Covariate data

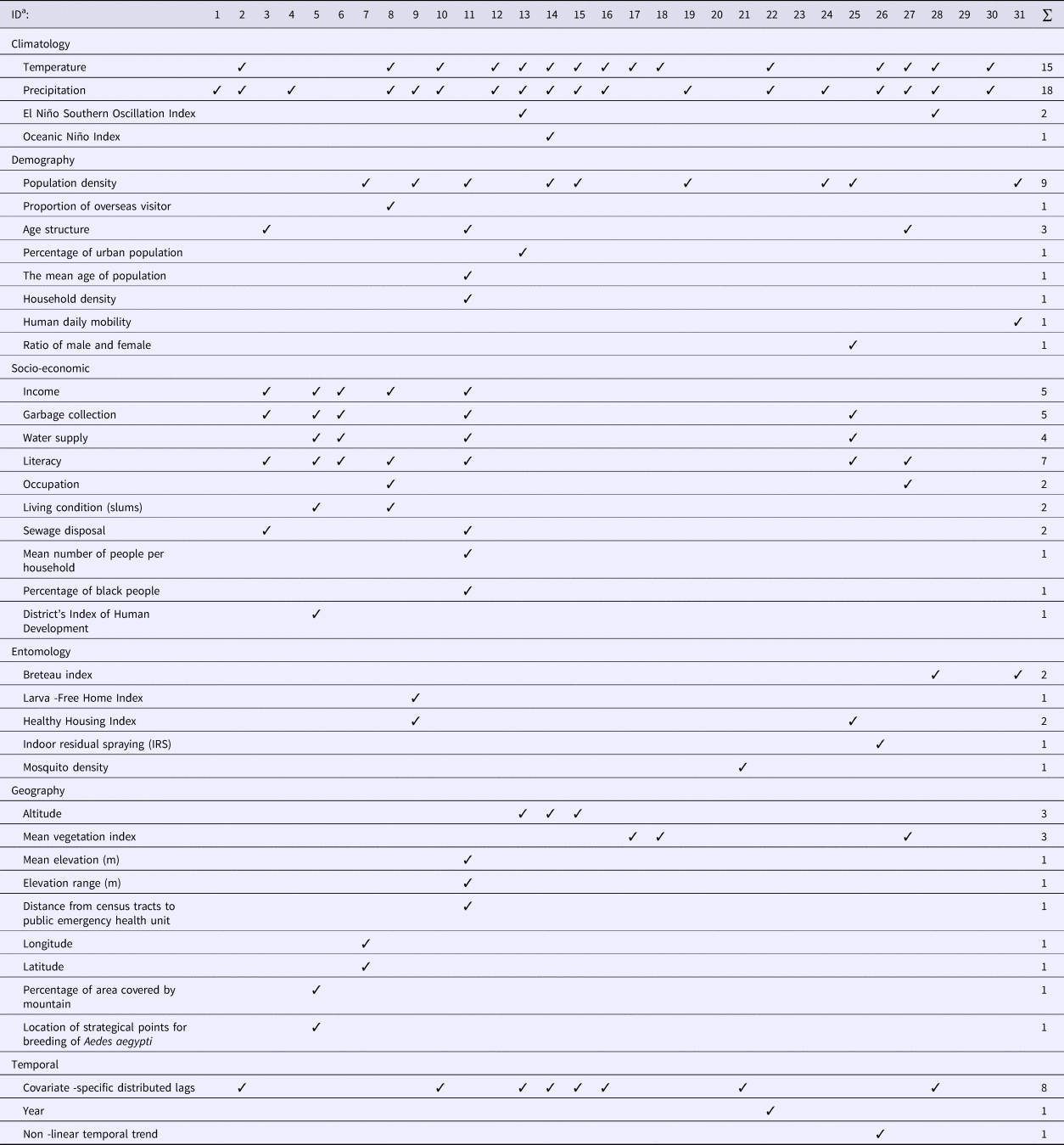
The type and number of covariates included in the models varied widely among the studies reviewed (Table 1). Six categories of covariates were identified, namely climatic, demographic, socio-economic, entomological, geographic and temporal. Although four studies [Reference Lowe26–Reference Wijayanti29] examined four of these categories of covariates, most studies used two or three categories while three studies did not include any covariates.

Table 1. Covariate variables used in reviewed papers

^a Refers to numbers in Table 2.

Table 2. Summary of the structure of the spatio-temporal models discussed in the reviewed paper

^a Spatial autoregressive (SAR).

^b Conditional autoregressive (CAR).

^c Cubic spline smoothing (CSS).

^d First-order autoregressive (AR(1)).

^e First-order random walk (RW1).

^f Besag–York–Mollié (BYM).

^g Penalised splines (P-splines).

^h Bayesian Maximum Entropy (BME).

Analytical method

A variety of Bayesian spatial and spatio-temporal approaches were used in modelling DF. Most studies adopted a fully Bayesian model with a spatially structured random effect using a CAR prior structure to investigate the relationship between the risk of dengue and selected covariates [Reference Jaya36, Reference Kikuti38–Reference Costa, Donalisio and Silveira41, Reference Ferreira and Schmidt43, Reference Martínez-Bello, Lopez-Quilez and Alexander Torres46]. Spatial empirical Bayes smoothing was used for two studies to examine the spatial distribution of dengue [Reference Vargas42, Reference Hu51].

Generalised linear mixed models (GLMMs) with proper CAR spatial random effects were applied to develop disease maps, with dengue incidence data assumed to be Poisson [Reference Lekdee and Ingsrisawang52]. Temporal components were additionally incorporated, either as a temporal covariate [Reference Pepin44, Reference Restrepo, Baker and Clements50], or via a GLMM with spatial and temporal random effects and temporal covariates [Reference Lowe26, Reference Lowe27, Reference Lowe48]. Among the selected studies, only two studies used a GLMM with spatial, temporal and spatio-temporal random effects [Reference Wijayanti29, Reference Martínez-Bello, López-Quílez and Prieto47], while one included these components along with an additional temporal covariate [Reference Lowe28]. Other GLMM spatio-temporal random-effects models with incorporation of a temporal trend have also been developed [Reference Sani35, 37]. Two studies used a GLMM zero-inflated model [Reference Fernandes, Schmidt and Migon33, 53].

Alternative models included estimation of relative risk for the transmission of dengue disease based on discrete time and space via a susceptible–infective-recovered model for human populations; susceptible–infective model for mosquito populations (SIR-SI) [Reference Samat and Percy54], prediction of spread of DF using Bayesian maximum entropy (BME) [Reference Yu30, Reference Yu55, Reference Yu, Lee and Chien56], and spatio-temporal quasi-Poisson model based on a DLNM (distributed lag non-linear model) [Reference Chien and Yu49], STARM (spatial–temporal autologistic regression model) [Reference Astutik34], hierarchical model with adaptive natural cubic spline [Reference Johansson, Dominici and Glass32], a semi-parametric Bayesian STAR (structured additive regression) model [Reference Vazquez-Prokopec31] and a transmission model based on Ross–Macdonald theory [Reference Zhu45]. The analytical methods used across all included studies are summarised in Supplementary Table S3 and summary of the structure of the spatio-temporal models discussed in the reviewed paper can be seen in Table 2. These models are explained in more detail as follows.

Spatial models

Several spatial models have been developed and applied to DF, namely empirical Bayes approaches and fully Bayes GLMM with a spatial CAR prior.

Empirical Bayes approaches: An empirical Bayes method is an approximation to the fully Bayesian method. In an empirical Bayes approach, the prior parameters are estimated from the data, while in a fully Bayesian analysis, the prior distribution is completely specified before observing any data [Reference Kumar57].

Empirical Bayes spatial smoothing for dengue incidence data has been used to categorise the high-risk and low-risk areas in Queensland [Reference Hu51]. Local empirical Bayes was applied to investigate the relationship between the HI, dengue incidence and socio-demographic variables [Reference Vargas42]. The authors concluded that there is a positive correlation between HI and Bayesian dengue incidence rate. The highest dengue risk regions were situated in the areas which had the highest population densities and were close to the major highways.

GLMM with spatial random effects: A GLMM with spatial random effects has been applied in seven studies [Reference Jaya36, Reference Kikuti38–Reference Costa, Donalisio and Silveira41, Reference Ferreira and Schmidt43, Reference Martínez-Bello, Lopez-Quilez and Alexander Torres46]. The general model is formulated as follows:

$$\eqalign{&y_i \sim {\rm Poisson}\lpar {\mu_i} \rpar \cr &\log \lpar {\mu_i} \rpar = \log \lpar {e_i} \rpar + \theta _i \cr &\theta _i = \; \alpha + \beta X\; + u_i + \; v_i} $$

where y _i is the number of dengue cases in i = 1, …, I areas; e _i and θ _i are, respectively, the expected number of dengue cases in area i and the log relative risk of dengue; α is the overall level of relative risk; β = (β ₁, β ₂, …β _p) represent the coefficient of the covariates; u _i is a spatially structured random effect with CAR prior structure and v _i is a spatially unstructured random effect with mean zero and variance $\sigma _v^2 $. All authors used an intrinsic Gaussian CAR (ICAR) prior and adopted a binary neighbourhood weighting. An ICAR model assumes the areas k and i are neighbours if both share a common border. This can be expressed as follows:

(1)$$\lpar {u_k{\rm \vert} u_i,\; k\ne i,\; \tau_u^2} \rpar \sim N\left( {\displaystyle{{\mathop \sum \nolimits_i u_i\omega_{ki}} \over {\mathop \sum \nolimits_i \omega_{ki}}},\; \displaystyle{{\tau_u^2} \over {\mathop \sum \nolimits_i \omega_{ki}}}} \right)$$

ω _ki = 1 if k, i are adjacent, ω _ki = 0 otherwise [Reference Riebler58, Reference Lawson59]. This prior is the most common Gaussian Markov random field [Reference Botella-Rocamora, López-Quílez and Martinez-Beneito60] and is an improper prior [Reference Lawson and MacNab61]. Allowing for spatial autocorrelation through this prior can improve model fit [Reference Kikuti38]. However, the choice of neighbourhood structure needs to be carefully considered as it could impact on the significance of some covariates [Reference Ferreira and Schmidt43]. One study examined two additional types of neighbourhood structure matrices, namely, weighted by the length of the boundary and by boundary and barriers [Reference Ferreira and Schmidt43].

Martínez-Bello et al. [Reference Martínez-Bello, Lopez-Quilez and Alexander Torres46] compared CAR BYM (Besag, York and Mollié) [Reference Besag, York and Mollié62] prior and Leroux CAR prior [Reference Leroux, Lei, Breslow, Halloran and Berry63] for spatially structured random effects for estimating relative risk of dengue. They found that the CAR BYM prior was better than the Leroux CAR prior.

Spatio-temporal models

GLMM over space and time with spatial random effects: A GLMM indexed by space and time and with spatial random effects has been proposed in one study [Reference Lekdee and Ingsrisawang52] to develop a disease map and identify any association between dengue incidence, rainfall and temperature. The proposed model is expressed as

$$\eqalign{y_{ij} \sim \; &{\rm Poisson}\lpar {\mu_{ij}} \rpar \cr \log \lpar {\mu_{ij}} \rpar = &\log \lpar {{\rm po}{\rm p}_i} \rpar + \alpha + \beta _1{\rm rai}{\rm n}_{ij} + \beta _2{\rm tem}{\rm p}_{ij}\; + u_i + \; v_i} $$

where y _ij are the number of dengue cases in area i = 1, …, I, and time j = 1, …, J; μ _ij is mean cases, log(pop_i) is the offset representing the total population in each area. Rain and temp are the total rainfall and temperature, respectively, in each area and time, and u _i are proper CAR spatial random effects. A proper CAR is a variant of the ICAR prior, with an additional term for spatial autocorrelation ρ in the conditional expectation [Reference Kandhasamy and Ghosh64], as follows:

$$\lpar {u_k{\rm \vert} u_l,\; k\ne l,\; \tau_u^2} \rpar \sim N\left( {\displaystyle{{\rho \mathop \sum \nolimits_l u_l\omega_{kl}} \over {\mathop \sum \nolimits_l \omega_{kl}}},\; \displaystyle{{\tau_u^2} \over {\mathop \sum \nolimits_l \omega_{kl}}}} \right)$$

If ρ = 1 then the model is the ICAR in equation (1).

GLMM with spatial random effects + temporal covariate: An alternative representation of a GLMM with spatial random effects and the inclusion of temporal covariates has been proposed in two studies [Reference Pepin44, Reference Restrepo, Baker and Clements50]. Restrepo et al. [Reference Restrepo, Baker and Clements50] found that the convolution model was the preferred model (this includes both u _i and v _i) over models containing only the uncorrelated termv _i or the ICAR term u _i, and precipitation was the most significant predictor of dengue risk.

Pepin et al. [Reference Pepin44] proposed a different GLMM formulation to assess the role of city-wide vector data in forecasting DF cases. In this model, they included the rate of cases in neighbourhood i at time j, mosquito density data, fixed scaling factors, lagged time for specific variables and different weighting functions between-neighbourhood effects to illustrate patterns of city-wide human movement which consists of economic value of the neighbourhood, population density and travel distance between neighbourhoods. Two scales of spatial disease data, that is, nearest-neighbourhood effects (local) and all between-neighbourhood effects (global) are compared to predict the association between mosquito density and human cases of dengue. Models that included global between-neighbourhood effects and two covariates (mosquito density and human cases of dengue) and their interaction were preferred.

GLMM with spatial and temporal random effects + temporal covariate: GLMMs with spatial and temporal random effects and a temporal covariate have been proposed in three studies [Reference Lowe26, Reference Lowe27, Reference Lowe48]. Lowe et al. [Reference Lowe26] compared a spatio-temporal GLM and a GLMM that includes random effects in the linear predictor and found that the latter model provided more accurate dengue predictions. In this model, the number of dengue cases y _ij are assumed to be Poisson distributed with mean dengue count μ _ij given by

$$\eqalign{\log \lpar {\mu_{ij}} \rpar = \, &\log \lpar {e_i} \rpar + \alpha + \mathop \sum \limits_k \beta _kx_{kij} \cr & + \; \mathop \sum \limits_k \gamma _kw_{ki} + u_i + v_i + \varphi _j} $$

where $u_i \sim {\rm CAR(}\sigma _u^2 {\rm )}$, $v_i \sim N{\rm (}0,\sigma _v^2 {\rm )}$, and φ _j are the temporally autocorrelated random effects (j = 2, …, 12) with φ ₁ = 0, and $\varphi _ j \sim N(\varphi _{j-1},\sigma _\varphi ^2 )$, j = 2, …, 12.

The variable climate factors x _kij are: precipitation in the previous 1 and 2 months, temperature in the previous 1 and 2 months and Nino 3.4 in the previous 6 months. The variables w _ki are: altitude and percentage of urban population.

Another spatio-temporal GLMM by Lowe et al. [Reference Lowe27] extended the model by Lowe et al. [Reference Lowe26] by adding more recent data and including log dengue standardised morbidity ratio in the previous 3 months (past dengue risk), spatially structured and unstructured random effects and a first-order autoregressive month effect. Here the DF counts y _ij are assumed to have a negative binomial distribution to allow for overdispersion in observed dengue data. The authors compared this model with a simple model based on past dengue risk only. They found that the extended model improved dengue predictions.

Generalised linear and additive mixed models (GLMM/GAMM) were applied to measure the benefit of including climate function in the model [Reference Lowe48]. The response had a negative binomial distribution and the dengue relative risk models included a baseline model with season only, a seasonal–spatial model (inclusion of spatial structure and unstructured error), a seasonal–spatial climate-linear model (linear climate model) and a seasonal–spatial climate-non-linear model (non-linear climate model). The results showed that the model with linear and non-linear climatic functions explained 39% and 40%, respectively, of the variation in dengue relative risk. An additional 7% and 8% of the variation was explained by seasonal–spatial structure using linear and non-linear climatic functions, respectively.

GLMM with spatial, temporal and spatio-temporal random effects + temporal covariate: Lowe et al. [Reference Lowe28] also formulated another GLMM model using a negative binomial distribution for the dengue case counts to predict dengue epidemic in Brazil during the 2014 football tournament. This model has minor differences and extensions to their previous model [Reference Lowe27]: the inclusion of log dengue standardised morbidity ratio 4 months previously, a fixed effect for month, a random effect for month and the inclusion of a first-order autoregressive month effect for each zone. Their results showed that this model can forecast which cities have low, medium and high risk of dengue.

GLMM with spatial, temporal and spatio-temporal random effects: Bayesian spatial, temporal and spatio-temporal random-effects models have been used to determine factors that influence the risk of dengue in the Banyumas regency, Indonesia [Reference Wijayanti29]. Two models have been compared, namely a model with the inclusion of covariates and spatially structured random effects only and a model with the inclusion of covariates, spatially structured and unstructured random effects, temporally structured and unstructured random effects and spatio-temporal random effects. The number of DF cases was assumed to be Poisson distributed. Uninformative priors were used for all variables as previous data were not available for Indonesia. The most significant factors that influenced the risk of dengue were found to be employment type and economic status. Wijayanti et al. [Reference Wijayanti29] explored only the unstructured interaction effect model (type I). The type II–IV interaction effects in spatio-temporal models of relative risk were not explored, which are temporal interactions, spatial interactions and inseparable space–time interactions, respectively. Martínez-Bello et al. [Reference Martínez-Bello, López-Quílez and Prieto47] explored type I–IV interaction effects, finding that the best model had the inclusion of a fixed coefficient of lag-zero epidemiological periods Land Surface Temperature (LST) and type IV interaction effects.

GLMM with spatio-temporal random effects + temporal trend: Sani et al. [Reference Sani35] developed a spatio-temporal convolution model as an extension of the spatial convolution model introduced by Eckert et al. [Reference Eckert65] and used this to analyse the relationship between covariates (rainfall and population density) and dengue risk. The number of dengue cases y _ij was assumed to be Poisson distributed and the relative risk μ _ij given by:

$$\eqalign{\log \lpar {\mu_{ij}} \rpar = &\log \lpar {e_{ij}} \rpar + \beta _0 + \mathop \sum \limits_k \beta _kx_{kij} \cr & + u_{ij} + v_{ij} + \lpar {\alpha + \delta_i} \rpar j_z} $$

where (α + δ _i)j _z is a temporal trend and

$${\rm \;} e_{ij} = \displaystyle{{\mathop \sum \nolimits_i \mathop \sum \nolimits_j y_{ij}} \over {\mathop \sum \nolimits_i \mathop \sum \nolimits_j n_{ij}}}n_{ij}$$

with n _ij denoting the number of population at area i time j.

The authors found that both rainfall and population density affected the number of dengue cases.

This spatio-temporal convolution model has been extended to include the probability of incident risk $\Pr \lpar {I_{ij}} \rpar $ into the model to overcome a misidentification of dengue location [37]. The extended model is as follows:

(2)$$\eqalign{{\rm log}(\mu _{ij}) = & \log (\Pr (I_{ij})) + \beta _0 + \mathop \sum \limits_k \beta _kx_{kij} + u_{ij} + v_{ij} \cr & + (\alpha + \delta _i)j_z}$$

where

$$\Pr \lpar {I_{ij}} \rpar = \displaystyle{{\mathop \sum \nolimits_i \mathop \sum \nolimits_j y_{ij}} \over {\mathop \sum \nolimits_i \mathop \sum \nolimits_j n_{ij}}}$$

This extension resulted in more accurate estimates when compared with the previous models [Reference Sani35, Reference Eckert65]. They also concluded that both rainfall and population density significantly affected the number of dengue cases.

GLMM zero-inflated Poisson spatio-temporal model: Zero-inflated spatio-temporal models that can be applied to both continuous and discrete data have been proposed [Reference Fernandes, Schmidt and Migon33]. When observations exhibit an excessive number of zero values, the zero-inflated model is often more appropriate. These have been applied to estimate the probability of the presence of unobserved dengue disease in region i and time j.

A Bayesian mixed zero-inflated Poisson spatio-temporal (BMZIP S-T) model [53] has also been constructed.

The BMZIP S-T model is expressed as

$$y_{ij} \sim {\rm Poisson(}\mu _{ij}{\rm )}$$

where μ _ij = ϕ _ij/(1 − ϕ _ij) and is modelled as per equation (2).

A spatio-temporal quasi-Poisson model: A spatio-temporal quasi-Poisson model based on the DLNM approach has been proposed to identify the relationship between the non-linear delayed impact of meteorological variations and dengue risk in southern Taiwan and to predict dengue cases in the coming weeks [Reference Chien and Yu49]. The number of weekly DF cases y _ij was assumed to have a Poisson distribution as follows.

$$\eqalign{{\rm log} (\mu _{ij}) = \; &{\rm offset} + \alpha + \beta \times \lpar {{\rm Year}} \rpar + f\lpar {{\rm Time}} \rpar \cr & + f\lpar {T,{\rm lag} = 20} \rpar + f\lpar {R,{\rm lag} = 20} \rpar + f_{{\rm spac}}\lpar d \rpar }$$

where the vector β contains the coefficients of the indicator variable year, f(Time) is the time smoother described by a cubic spline; f(T, lag = 20) and f(R, lag = 20) are functions of temperature and rainfall with a maximum temporal lag of 20 weeks, respectively; f _spac(d) is a spatial function which was modelled using the CAR prior structure, and the offset is the logarithm of average annual population data. The authors found that the most significant factors that influenced DF epidemics were the weekly minimum temperature and the maximum 24 h rainfall. When the minimum temperature rises, the dengue relative risk increases, particularly at a lagged period of 5–18 weeks.

Hierarchical model with adaptive natural cubic spline: Johansson et al. [Reference Johansson, Dominici and Glass32] proposed a model that includes population size N _j, covariates at distributed lags l _k and a natural cubic spline smoothing function of time s(j, λ), where λ denotes the degree of annual freedom and is set to λ = 2. The distributed lag model is used to evaluate the effect of weather on dengue spread in the next 6 months. For each area i, the number of monthly dengue cases at time j, y _j, is assumed to be Poisson distributed as follows:

$$\eqalign{y_j \sim &{\rm Poisson(}\mu _j{\rm )} \cr \log (\mu _j) = &\log \lpar {N_j} \rpar + \beta _0 + \mathop \sum \limits_k \beta _kx_{k,j-l_k} + s\lpar {\,j,\lambda} \rpar } $$

A two-level approach was used to compare β _k from the area-specific models. At the first level, area-specific (i) parameter estimates $\hat{\beta} _i$ were assumed to be normally distributed:

$$\hat{\beta} _i \sim N\lpar {\beta_i,\sigma_i^2} \rpar $$

Effect modifiers z ₁, z ₂, …, z _Q were added to estimate α ₀ (the average effects) and the effect modification α _q:

$$\beta _i\left \vert {\alpha_0,\alpha_1, \ldots, \alpha_Q,\sigma^2 \sim N\left( {\alpha_0 + \mathop \sum \limits_{q = 1}^Q \alpha_qz_{q,i},\sigma^2} \right)} \right.$$

The authors found a positive correlation between monthly variation in temperature and precipitation and monthly variation in the spread of dengue, and that correlation varies spatially.

BME method: BME is popular in the study of natural systems (physical, biological, social or cultural) and for attributes that are characterised by space–time dependence and multi-sourced uncertainty. Two major knowledge bases (KB) for the spatio-temporal modelling in the BME method are: (1) the general KB (G-KB) that may include scientific theories, theoretical space–time dependence models and epidemic models; and (2) the site-specific KB (S-KB) that includes hard data and soft data, often with a significant amount of uncertainty [Reference Kanevski66]. The BME method incorporates both knowledge bases [Reference Christakos67, Reference Christakos68].

A spatio-temporal model that is based on a stochastic BME method has been used to predict DF outbreaks based on space and time and to examine the association between DF incidence and selected climate variables in Southern Taiwan [Reference Yu30]. In the BME analysis, the spatio-temporal distribution of DF occurrences is mathematically represented by the spatio-temporal random field, X(p) or X _i,j where i and j indicate the areas and time, respectively. DF incidence is assumed to be Poisson distributed as follows:

$$X\lpar {\bi p} \rpar = X_{ij} \sim {\rm Poisson}\; \lpar {R_{ij}\lambda_{ij}} \rpar $$

with DF mean $\bar{X}_{ij} = R_{ij}\lambda _{ij}$ and λ _ij is a climate-driven space–time process modelled by the log-link Poisson regression

$$\eqalign{\log \lpar {\lambda_{ij}} \rpar = \; &\log \lpar {n_{ij}} \rpar + \alpha _0 + \mathop \sum \limits_{l = a}^b \beta _lT_{\,j-l} + \mathop \sum \limits_{m = c}^d \gamma _m\log \lpar {T_{\,j-l}} \rpar \cr & + \mathop \sum \limits_{n = e}^f \theta _nSOI_{\,j-n} + \mathop \sum \limits_{o = g}^h \rho _o{\rm \;} Bidx_{\,j-o} + \mathop \sum \limits_{\,p = r}^s \phi _p\; \max T_{\,j-p} \cr & + \mathop \sum \limits_{q = t}^u \varphi _q \min T_{\,j-q}\;} $$

where β _l, γ _m, θ _n, ρ _o, ϕ _p and φ _q are regression coefficients for temperature, logarithm of rainfall, SOI, BI, maximum temperature and minimum temperature, respectively (for the weekly temporal lags between a and b, c and d, e and f, g and h, r and s, and t and u, respectively) and n _ij is the population size. The authors conclude that climatic conditions significantly affect DF outbreaks. Yu et al. [Reference Yu55] extended their previous model by inclusion of a stochastic susceptible–infected–recovered (SIR) model, that is, BME-SIR to obtain online space–time predictions of DF transmission. This model considered stochastic differential equations, characterising both the spatio-temporal pattern of disease spread and the heteroscedastic variance pattern across space and time. The aim was to achieve online updates of SIR model parameters.

A SIR-SI model: A discrete space–time stochastic susceptible–infective–recovered for human populations; susceptible–infective for mosquito populations (SIR-SI) model has been developed to circumvent problems of relative risk estimation using standardised morbidity ratios and the Poison-γ model which does not allow for spatial correlation [Reference Samat and Percy54]. The SIR-SI model was defined as follows:

$$\eqalign{S_{i,j}^{\lpar h \rpar } = \; &\mu ^{\lpar h \rpar }N_i^{\lpar h \rpar } + \lpar {1-\mu^{\lpar h \rpar }} \rpar \lpar {S_{i,j-1}^{\lpar h \rpar }} \rpar -{\rm \Im} _{i,j}^{\lpar h \rpar } \cr {\rm \Im} _{i,j}^{\lpar h \rpar } \sim \; &{\rm Poisson\;} \lpar {\lambda_{i,j}^{\lpar h \rpar }} \rpar \cr \lambda _{i,j}^{\lpar h \rpar } = \; &\exp \lpar {\beta_0^{\lpar h \rpar } + c_i^{\lpar h \rpar }} \rpar \left( {\displaystyle{{\beta^{\lpar h \rpar }b} \over {N_i^{\lpar h \rpar } + m}}} \right)I_{i,j-1}^{\lpar h \rpar } S_{i,j-1}^{\lpar h \rpar }, \cr I_{i,j}^{\lpar h \rpar } = \; &\lpar {1-\mu^{\lpar h \rpar }} \rpar I_{i,j-1}^{\lpar h \rpar } + {\rm \Im} _{i,j}^{\lpar h \rpar } -{\rm \Re} _{i,j}^{\lpar h \rpar } \cr R_{i,j}^{\lpar h \rpar } = \; &\lpar {1-\mu^{\lpar h \rpar }} \rpar R_{i,j-1}^{\lpar h \rpar } + {\rm \Re} _{i,j}^{\lpar h \rpar } \cr {\rm \Re} _{i,j}^{\lpar h \rpar } = \; &\gamma ^{\lpar h \rpar }I_{i,j-1}^{\lpar h \rpar }} $$

with a non-stochastic vector population as follows:

$$\eqalign{S_{i,j}^{\lpar v \rpar } = \; &\mu ^{\lpar v \rpar }N_i^{\lpar v \rpar } + \lpar {1-\mu^{\lpar v \rpar }} \rpar \lpar {S_{i,j-1}^{\lpar v \rpar }} \rpar -{\rm \Im} _{i,j}^{\lpar v \rpar } \cr {\rm \Im} _{i,j}^{\lpar v \rpar } = \; &\; \left( {\displaystyle{{\beta^{\lpar v \rpar }b} \over {N_i^{\lpar v \rpar } + m}}} \right)I_{i,j-1}^{\lpar v \rpar } S_{i,j-1}^{\lpar v \rpar } \cr I_{i,j}^{\lpar v \rpar } = \; &\lpar {1-\mu^{\lpar v \rpar }} \rpar I_{i,j-1}^{\lpar v \rpar } + {\rm \Im} _{i,j}^{\lpar v \rpar }} $$

Here the superscripts (h) and (v) represent the human and mosquito populations, respectively. $S_{i,j}^{\lpar h \rpar }, \; I_{i,j}^{\lpar h \rpar } $ and $R_{i,j}^{\lpar h \rpar } $ are the total number of susceptible, infective and recovered humans in area i for time j, respectively; ${\rm \Im} _{i,j}^{\lpar h \rpar } $ and ${\rm \Re} _{i,j}^{\lpar h \rpar } $ are the number of newly infective and recovered humans; μ ^(h) is the weekly birth and death rates in the human population; γ ^(h) is the rate of weekly recoveries; b is weekly biting rate; m is the number of alternative hosts available; β ^(h) is the probability of transmission from mosquito to human, and β ^(v) is the converse; and $N_i^{\lpar h \rpar } $ is the number of humans in area i.

The number of new infections is assumed to follow a Poisson distribution with mean $\lambda _{i,j}^{\lpar h \rpar } $, intercept $\beta _0^{\lpar h \rpar } $ and spatial random effect $c_i^{\lpar h \rpar } $ using a CAR prior. Models were applied to all of Malaysia divided into 16 states. The results showed that the proposed SIR-SI model that considers the inclusion of the transmission process of dengue disease, covariates and spatial correlation was preferred over unmodelled SMRs or the Poisson-γ model. The authors also identified areas with very high and high dengue risk.

STARM: The STARM model is an extension of an autologistic regression model that includes covariates, spatial and temporal dependence simultaneously. This model has been applied to predict the association between the incidence of endemic dengue and rainfall using a Bayesian method [Reference Astutik34]. For binary data that are measured repeatedly on a spatial lattice, STARM can be very beneficial [Reference Zheng and Zhu69]. The incident rate (IR) is converted to the binary scale as a representation of the A. aegypti spread, that is, 1 if there is endemic dengue (IR > 10/100 000 population) and 0 if there is no endemic dengue. Endemic level and rainfall are dependent and independent variables, respectively. The STARM model may be defined as follows:

$$p\lpar {Y_{i,j}{\rm \vert} Y_{\^{\prime}i,}_{\mathop j\limits^\^{\prime}} :\lpar {\^{\prime}i, \mathop j\limits^\^{\prime}} \rpar \ne \lpar {i,j} \rpar } \rpar = p\lpar {Y_{i,j}{\rm \vert} Y_{\^{\prime}i, \mathop j\limits^\^{\prime}} :\lpar {\^{\prime}i, \mathop j\limits^\^{\prime}} \rpar \in N_{i,j}} \rpar = \displaystyle{{{\rm exp}\left\{ {\theta_0Y_{i,j} + \theta_1X_{1,i}Y_{i,j} + \mathop \sum \nolimits_{k\in N_i} \theta_2Y_{i,j}Y_{k,j} + \theta_3Y_{i,j}(Y_{i,j-1} + Y_{i,j + 1})} \right\}} \over {1 + {\rm exp}\left\{ {\theta_0Y_{i,j} + \theta_1X_{1,i}Y_{i,j} + \mathop \sum \nolimits_{k\in N_i} \theta_2Y_{i,j}Y_{k,j} + \theta_3Y_{i,j}(Y_{i,j-1} + Y_{i,j + 1})} \right\}}}.$$

where Y _i,j is dengue endemic at the ith region and the jth time, X _1,i is rainfall index at the ith region, N _i,j is neighbourhood structure. θ ₀, θ ₁, θ ₂, θ ₃ are an intercept and coefficients for rainfall, spatial autoregression and temporal autoregression, respectively. The authors use the inverse Gaussian as a prior distribution for each of θ ₀, θ ₁, θ ₂, θ ₃. The result showed that there is a positive correlation between the endemic level of DHF incidence and rainfall.

A semi-parametric Bayesian spatio-temporal geoadditive STAR model: A spatio-temporal geoadditive STAR model has been used to evaluate the impact of indoor residual spraying and spatial autocorrelation in the odds of dengue infection [Reference Vazquez-Prokopec31]. A predictor structure for the spatio-temporal geoadditive model is given as follows:

$$\eta _{ij} = f_1\lpar {x_{ij1}} \rpar + \cdots + f_k\lpar {x_{ijk}} \rpar + f_{{\rm time}}\lpar j \rpar + f_{{\rm spat}}\lpar {s_{ij}} \rpar + {u}^{\prime}_{ij}\gamma $$

where η _ij, x _ij1, …, x _ijk are predictor and covariate values for individual i at time j. The fixed effects of non-linear function of covariates (f ₁, …, f _k) and non-linear time trend f _time were modelled by independent diffuse priors using Bayesian penalised splines. f _spat is a spatially structured random effect of the location s _ij using Markov random field priors and ${u}^{\prime}_{ij}\gamma $ are linear predictors for the covariate vector u.

This STAR model assessed the impact of rain, spray cumulative proportion (cum_spr) and spatial correlation (spat) on the odds of dengue virus infection, where the probability of infection followed a binomial distribution (0 if there is no infection, 1 if there is an infection) at house level (1490 premises) as follows:

$$\eqalign{{\rm logit\;} \lpar {{\rm case},0{\rm \vert} 1} \rpar = \; &f_{{\rm time}} + {\rm rain}\; \lpar {{\rm fixed}} \rpar + f_1\lpar {{\rm cum}\_{\rm spr}} \rpar \cr & + f_{{\rm spat}} + f_2\lpar {{\rm cum}\_{\rm spr{^\ast}spat}} \rpar } $$

The authors compared two STAR models, that is, a model with and without rain as a fixed effect. Interestingly the results showed that a model without a rain covariate was better able to describe the spatial pattern of dengue infection. The authors concluded that there was a significant positive correlation between the number of indoor residual spraying applications up to a time lag of 2 weeks and the weekly number of cases.

Transmission model based on Ross–Macdonald theory: A dengue transmission model based on the Ross–Macdonald theory has been proposed to identify the pattern of dengue transmission in space and time. This model incorporates four essential sub-models, that is, female mosquito density dynamics, human daily movement, virus transmission and estimation of parameters [Reference Zhu45] that can be explained as follows.

The correspondence between reported incidence and modelling cases is given as follows:

$${\rm \Gamma} _j = \delta \rho _j + \varepsilon _j;\quad \varepsilon _j \sim N\lpar {0,{\rm \Sigma}} \rpar $$

where δ is reported incidence rate, ρ _j = (ρ _1j, ρ _2j, …, ρ _Ij)^J is a vector of the estimated number of incidences at each time period j, ε _j is an error term and Γ_j = (γ _1j, γ _2j, …, γ _Ij)^J is the vector space–time surveillance data at time j.

Female mosquito density $x_i^k \lpar j \rpar $ with age k at time j in district i can be calculated as

$$x_i^k \lpar j \rpar = KB_i\lpar {\,j-k-1} \rpar p\lpar k \rpar $$

where K is the proportionality coefficient between the vector density and BI, B _i(j) is the value of BI at time j in district i, p(k) is the daily survival probability of adult mosquitoes at age k. To estimate model parameter K, MCMC methods were used.

Human daily commuting into different areas, which is defined as those who work or study in different districts and who go out in the morning and return in the afternoon, is assumed to impact on dengue transmission as follows:

$$T_{il} = T_i\displaystyle{{N_iN_l} \over {\lpar {N_i + S_{il}} \rpar \lpar {N_i + N_l + S_{il}} \rpar }}$$

where T _il is the number of travellers leaving from district i to l; N _i is the population in district i; S _il is the total number of residents in the circle whose centre is the origin district i and radius is the distance between district i and the destination district l, minus the population at i and l. T _i is the total number of travellers leaving from district i which is defined as T _i = N _i(N _c/N), where N _c and N are the total number of travellers and the total population, respectively.

In virus transmission modelling, vectorial capacity, which is defined as the mean of infectious mosquito bites per unit time, is used to evaluate the infectivity from mosquitoes and is calculated as

$$V_i^k \lpar j \rpar = m_i^k \lpar j \rpar a_i^2 e^{k + q}\mathop \prod \limits_{l = k}^{k + q} p\lpar l \rpar $$

where $V_i^k $, $m_i^k $ represent vectorial capacity contributed by mosquitoes with age k in district i, and the ratio of mosquitoes at age k to humans, respectively. Here a _i and e ^k+q represent Aedes mosquito biting rate of humans in district i within 12 h, and the expectation of remaining infectious life at age k + q, respectively.

The authors concluded that the space–time distribution of incidence is highly heterogeneous, with 81.6% of transmission occurring in urban centres in Guangzhou, China with a peak in mid-October. They also found that there is inconsistency between infected cases and reported cases in space–time. Vector indices and human mobility factors significantly affect the dengue transmission patterns. Urban areas had the highest incidence rates and suburban areas had the second highest incidence rates.

Assessment of quality

Using the adapted tool for assessment of modelling study quality, quality scores for the reviewed paper ranged from 7 to 16 out of 16 (Table 3). One study was classified as low quality, three as medium quality, 10 as high quality and 17 as very high quality. The median score was 14/16, which is categorised as high quality. Details on the quality of data were lacking in many papers.

Table 3. Assessment of included modelling studies

AaO, aims and objectives; SaP, setting and population; MS, model structure; MM, modelling methods; PRDS, parameter ranges and data sources; QoD, quality of data; PoR, presentation of results; IDoR, interpretation and discussion of results; FS, final score.