INTRODUCTION
Infection by dengue virus causes a wide variety of illnesses ranging from rarely lethal dengue fever (DF) to dengue haemorrhagic fever (DHF), the latter of which results in a case-fatality rate of more than 10% unless adequately treated [Reference Kalayanarooj1, 2]. With no approved vaccine available, reduction of vector mosquitoes has been regarded as the only means of controlling dengue. However, whether mosquito control has actually reduced dengue illnesses is under debate. Reduction of vector mosquitoes results in a higher average age at which primary infections occur [Reference Anderson and May3]. Since primary infections often are asymptomatic in children but manifest as illness in adults [Reference Dantes4, Reference Egger and Coleman5], this rise in host age appears to have increased the incidence of DF in Singapore [Reference Egger6]. As the average age of dengue infection is increasing in many countries [Reference Guha-Sapir and Schimmer7], this mechanism, known as ‘endemic stability’ [Reference Coleman, Perry and Woolhouse8], may explain the rising incidence of DF in some countries.
The unique immunological aetiology of DHF may have led to a similar unwanted consequence as well [Reference Nagao and Koelle9]. DHF is known to occur in a secondary infection more frequently than in a primary infection, due to immunological mechanisms including antibody-dependent enhancement (ADE) [Reference Halstead, Shotwell and Casals10]. On the other hand, many of the individuals in areas of high vector mosquito abundance would be infected by, and acquire immunity against, multiple serotypes while they are clinically protected by this cross-immunity [Reference Sabin11]. Consequently, these individuals develop resistance to DHF unknowingly, since those infected by more than one serotype rarely manifest DHF [Reference Sangkawibha12]. As mosquito abundance decreases, an increasing number of individuals would experience secondary infections after the protective cross-immunity has waned, and the incidence of DHF would increase. Consistent with this hypothesis, incidence of DHF was in a negative relationship with mosquito abundance in Thailand [Reference Nagao and Koelle9, Reference Thammapalo13].
Whether these seemingly paradoxical hypotheses are true or not, the concern that insufficient mosquito control may increase the incidence of DF and DHF underscores the importance of understanding the effect of mosquito control and future vaccination on the target population. In effect, two tetravalent live vaccines were developed and tested in clinical trials: a classical live-attenuated vaccine from the Walter Reed Army Institute of Research (WRAIR) [Reference Sun14] and a chimeric yellow fever–dengue composite vaccine (ChimeriVax or CYD) from Sanofi-Pasteur [Reference Guy15]. Of these, only CYD remained in phase II b trials [Reference Sabchareon16]. However, dengue vaccines harbour a unique concern: enhancing antibodies may be induced by the vaccine itself [Reference Morens17, Reference Huisman18]. In particular, a classical live-attenuated vaccine, which induces immune responses similar to those induced by wild-type viruses [Reference Guy19], may predispose a vaccinee to the risk of enhancement upon a subsequent infection. The risk of inducing enhancement by CYD, which is a yellow fever vaccine framework inserted with prM and E genes from dengue viruses, is regarded as being less than for classical live-attenuated vaccine [Reference Guy19]. However, ‘only phase IV trials and post-marketing surveillance will provide a definitive answer as to whether ADE constitutes a risk for vaccinees’ [Reference Guy15]. Therefore, seroconversion to all four serotypes is regarded as a prerequisite for a tetravalent dengue vaccine. By contrast, in clinical trials conducted to date, live tetravalent vaccines induced antibodies to less than four serotypes in a considerably large proportion of vaccinees, even after two consecutive injections [Reference Poo20, Reference Morrison21]. Although seroconversions to all four serotypes were achieved after three injections, such a three-dose regimen of a live vaccine is unprecedented. Furthermore, administering all three doses to all vaccinees may be difficult to achieve in developing countries.
It is recognized that mathematical models are useful to predict the population-level effects of dengue vaccine [Reference Beatty22]. Alternatively, the present study used an individual-based model, based upon results from clinical trials. Mathematical models creates a set of differential equations. In contrast, individual-based models create a large number of human individuals in the computer's memory, and observes their behaviour [Reference Grimm23]. Diverse scenarios, regarding seroconversion rates of dengue vaccine and vaccination coverage were compared. In addition, the incidence of DHF attributable to ADE derived from prior vaccination was estimated. Finally, the optimal strategy for dengue control is discussed.
MATERIALS AND METHODS
Assumptions for protective and enhancing antibodies
While the titre of antibodies against dengue virus is high, the protective role of antibodies is dominant: however, as the titre wanes, antibodies enhance development of DHF [Reference Kliks24]. It is not known whether protective antibodies and enhancing antibodies are physically separable (Fig. 1 a) ([Reference Brandt25] and E. Konishi et al., personal communication), or whether the same antibodies switch from protection to enhancement as their titres wane − in other words, virtual enhancing antibody (Fig. 1 b) [Reference Morens, Halstead and Marchette26]. However, these two hypotheses converge into an identical software coding if the first hypothesis (Fig. 1 a) surmises that the enhancing antibody persists life-long and if the second hypothesis (Fig. 1 b) assumes that antibody induced by viral inoculation exerts life-long enhancement. This framework enabled the distinction between enhancing antibodies induced by prior wild-type infection and those attributable to vaccine.

Fig. 1. Two hypotheses regarding antibodies to dengue viruses. (a) Enhancing antibodies and protective antibodies are different. Enhancing antibodies react with all virus serotypes (broken arrows). In contrast, protective antibodies are specific to a serotype (D1 in this figure), but exert transient cross-reactive protection against other serotypes (solid arrows). (b) The same antibodies may play different roles in protection and enhancement, depending on their titres. Antibodies (specific to D1 in this figure) exert protection against other serotypes when their titres are high (solid arrows). As the titre wanes, these antibodies act as enhancing antibodies (broken arrows). D1, D2, D3, and D4 represent dengue virus serotypes 1, 2, 3, and 4, respectively.
An inoculation with a wild-type virus induces protective antibodies specific to that serotype. On the other hand, an individual inoculated with a tetravalent live vaccine acquires protective antibodies specific only to the serotype(s) to which s/he seroconverted. The protective antibodies are assumed to exert life-long serotype-specific protection, as well as transient cross-serotype protection for a duration of C years from the latest inoculation. Sabin [Reference Sabin11] observed volunteers who were inoculated sequentially with two different strains of dengue virus, with the interval between the inoculations being maximally 9 months. It was found that cross-protection against severe illness still persisted at least after this interval. In addition, vaccination with yellow fever–dengue 2 chimeric vaccine induced cross-serotype protection that lasted >1 year [Reference Guirakhoo27]. Furthermore, it was reported that secondary infections resulted in DHF, DF, and asymptomatic infections at 2·6, 1·9, and 1·6 years after the primary infections, respectively [Reference Anderson28]. These observations suggested that cross-serotype protection against DHF may last for >1 year. Therefore, C was assumed to follow a normally distributed probability distribution function (PDF) with a mean equal to 2 years (Table 1). An individual inoculated with either wild-type or vaccine acquires enhancing antibodies, which persist throughout that individual's life [Reference Guzman29, Reference Gonzalez30].
Table 1. Variable parameters given to simulations

PDF, Probability distribution function with normal distribution; s.d., standard deviation.
* Fixed, a fixed value was input into each simulation to examine the effect of the parameter on the simulation result.
Table 2. Serotype-specific seroconversion rates (%) of CYD tetravalent dengue vaccine based on a PRNT50 of 1:10, obtained from clinical trials conducted in non-endemic areas

D1, D2, D3, and D4 represent dengue virus serotypes 1, 2, 3, and 4, respectively.
Assumptions for DF and DHF
Individual-based model simulation software (detailed in Protocol S1 of reference [Reference Thammapalo13]) was modified to describe immunological behaviour of the host (Fig. 2 a). When a naive individual is inoculated by wild-type dengue virus, s/he transitions to the cross-protected state. In the course of this transition, s/he may develop DF with an age-dependent probability defined in Figure 2 b (constructed based upon reference [Reference Egger and Coleman5] and P. G. Coleman, personal communication), and DHF with a fixed small probability of 0·2% [Reference Sangkawibha12]. If an individual in the cross-protected state is inoculated with a virus serotype, s/he acquires antibodies specific to this serotype and remains in the cross-protected state. C years after the most recent inoculation, the individual moves to the expired cross-protection state. When an individual in this state is inoculated with a serotype to which s/he does not possess specific antibodies (i.e. unexperienced serotype), s/he may manifest DF. The individual may also develop DHF with an enhanced probability of 4% [Reference Sangkawibha12], if s/he already possesses enhancing antibodies. An individual who has seroconverted to ‘L’ serotype transitions to the completely immune state (Table 1). The transmissibility (or viraemia) may be enhanced ‘T’-fold during manifestation of DHF [Reference Vaughn31] (Table 1).

Fig. 2. Individual-based model for dengue infections. (a) Diagram of the transition between immunological states. Transition between immunological states (filled arrow) occurs as a result of either viral inoculation or expiration of time from the most recent inoculation (open arrow). During a state transition, the individual may manifest dengue fever (DF) or dengue haemorrhagic fever (DHF) (arrow head). * A modification of the model in reference [Reference Thammapalo13] was made: the individual is predisposed to the risk of DHF only if enhancing antibodies pre-exist. (b) Age-dependent probability for an infection to manifest as DF in an individual who is not protected specifically or cross-reactively. The probability is expressed as: 100/[1 + 1/exp(−3·44 + 0·177 × age)] % ([Reference Egger and Coleman5] and P. G. Coleman, personal communication).
Basic and effective reproductive numbers
In the mathematical models for dengue proposed so far, transmission intensity was often expressed as mosquito density [Reference Wearing and Rohani32, Reference Chikaki and Ishikawa33] or as basic reproductive number (R 0) [Reference Nagao and Koelle9, Reference Massad34, Reference Coelho35]. In the present study, R 0 represents transmission intensity, since R 0 is proportional to vector abundance [Reference Anderson and May3, Reference Macdonald36, Reference Macdonald37]. The range of R 0 was selected, considering previous estimates [Reference Massad34, Reference Ferguson, Donnelly and Anderson38, Reference Johansson, Hombach and Cummings39].
The immunological state of each individual was updated at discrete time-steps of 2 weeks' length, which approximates the sum of intrinsic incubation and infectious periods [Reference Sabin11, Reference Vaughn31, Reference Gubler40]. The risk of being infected by a serotype (force of infection or viral inoculation rate) at the ith time-step (F i ) was obtained as:
where R 0,i−1, U i−1 and N i−1 represent basic reproductive number, viraemic load and population size in the (i−1)th time-step, respectively. Here, the viraemic load at the ith time step (U i ) is defined as:
where DF i and DHF i denote the number of patients with DF and DHF, respectively. T is the above-mentioned enhancement in transmissibility (Table 1). Effective reproductive number, which is defined as the secondary infectious cases originating from a primary infectious case, was estimated for each time step to be compared with R 0 given to the simulation.
Estimation of vaccine seroconversion rates
To exclude the effect of natural infections, the results of clinical trials conducted in non-endemic areas were used in the present study (Table 2). Two trials adopted a regimen of 0–3·5–12 months [Reference Poo20, Reference Morrison21]. However, the short first interval resulted in trans-serotype interference [Reference Guy15, Reference Morrison21]. Therefore, the present study assumed 0–6–12 months interval (Table 3). The results in adult vaccinees were applied to paediatric vaccinations. All the trials in Table 2 defined a 50% plaque reduction neutralization titre (PRNT50) of 1:10 as the cut-off for seropositivity. This titre had been considered as the surrogate for maximal protection, as in Japanese encephalitis [Reference Hombach41]. The clinical studies reported the seroconversion rate after the first dose (R i ,1%), that after the second dose (R i ,1 + 2%) and that after the third dose (R i ,1 + 2+3%) for each serotype i (i = 1, 2, 3, or 4). From these values, the seroconversion rate achieved solely by the second dose (R i ,2) was estimated as:
Similarly, the seroconversion rate achieved solely by the third dose (R i ,3) was estimated as:
Here, it was assumed that vaccinees that had seroconverted would not turn seronegative.
Table 3. Dengue serotype-specific seroconversion rates (%) assumed in simulations
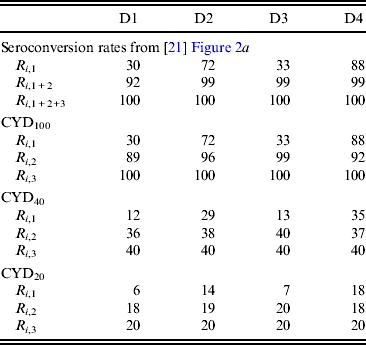
R i,1, R i,1 + 2 and R i,1 + 2+3 denote the seroconversion rate for serotype i after the first, second, and third doses, respectively. R i,2 and R i,3 represent the seroconversion rate achieved solely by the second and third doses, respectively. R i,2 and R i,3 of CYD100 were estimated using equations (3) and (4) in the main text, respectively. R i,1, R i,2, and R i,3 of CYD40 and those of CYD20 were 40% and 20% of the corresponding values for CYD100, respectively. R I,1, R i2 and R i,3 were input into the simulations. D1, D2, D3, and D4 represent dengue virus serotypes 1, 2, 3, and 4, respectively.
Compromised protective seroconversion rates
R i,j (i = 1−4, j = 1−3) represents the maximal achievable protective potencies. However, the efficacies reported in the clinical trial were low (i.e. 30·2%) [Reference Sabchareon16], indicating that ‘protective’ seroconversion rates for CYD may be much lower than R i,j , which was measured based on a PRNT50 of 1:10. Therefore, the present study conducted a sensitivity analysis by considering tetravalent vaccines with compromised protective potencies (Table 3). CYD40 and CYD20 were assumed to induce protective seroconversion rates of 40% and 20%, respectively, compared to the seroconversion rates measured as PRNT50 of 1:10. CYD100 induces protective seroconversion rates equal to those measured as PRNT50 of 1:10.
Vaccine assumptions
Enhancing antibodies derived from vaccine and those from wild-type virus were differentiated in the software. Inoculation by a vaccine will not manifest as clinical illness or lead to development of transmissible viraemia. Since CYD tetravalent vaccine contains only two dengue-virus peptides (E and prM), this vaccine may not confer efficient cross-protection. Consistent with this assumption, the efficacy of CYD measured within 2 years after vaccination was only 30% [Reference Sabchareon16]. Therefore, this study adopted an unfavourable scenario for CYD, assuming that CYD does not induce cross-serotype protection.
Emulation of vaccination programme
A future vaccination programme was emulated. At the 100th year in a 150-year simulation, a vaccination programme was initiated. After this year, an attempt was made to vaccinate all children who reached age 2 years but only with a successful coverage of V%. This age was selected because it was the youngest age tested in the clinical trials so far conducted. It was attempted to re-vaccinate the vaccinees at 6 months and 12 months after the first dose, but with a successful follow-up coverage of V%, respectively. This was because 100% accomplishment of any vaccination programme, especially of three-dose regimen, is difficult to achieve in developing countries.
Inhomogeneous mixing
The degree of inhomogeneity in the mixing pattern was represented by I, where I = 0 indicated completely homogeneous mixing and I = 1 indicated maximally inhomogeneous mixing (see Supplementary online Appendix 1 and Table 1).
Seasonality
Since vector mosquito abundance fluctuates seasonally [Reference Strickman and Kittayapong42], seasonality is an important factor which should be considered in modelling a mosquito-borne disease [Reference Chikaki and Ishikawa33]. Therefore, the present study expressed seasonality as a sinusoidal function of R 0, as follows:
where θ represents the phase of a time-step in a year [0 ⩽ θ⩽ 2π], R
0(θ) indicates R
0 at this phase, and
![]() $\bar R_0 \; $
expresses the average annual R
0. S represents the strength of seasonality. S = 1 indicates the strongest seasonality and S = 0 represents no seasonality (Table 1).
$\bar R_0 \; $
expresses the average annual R
0. S represents the strength of seasonality. S = 1 indicates the strongest seasonality and S = 0 represents no seasonality (Table 1).
Age-specific birth rate and mortality rate
Demographic data from Thailand were used as an example of a region heavily afflicted by dengue. Age-population structure of Thailand in 1960 was used as the initial population structure. Population growth was represented by the total fertility rate (TFR) [Reference Russel and Cohn43]. Based on the TFR given to a simulation, age-specific birth rate was reconstructed for the each age class of females (Supplementary Appendix 2). The age-specific mortality rate reported from Thailand in 2005 was used throughout the entire simulation. TFR of Thailand was 1·86 in 2000.
Source code
The source code, which was written in PERL language, can be obtained from Supplementary Appendix 3.
RESULTS
Effects of vaccination and vector control on the incidence of DF and DHF
As a result of simulations, the viral inoculation rate (or force of infection) decreased linearly as the mosquito abundance (represented by R 0) decreased or as the vaccination coverage increased (Fig. 3 a–c). However, the behaviour of the incidence of DF and DHF was more complex. A steep high ridge of DF incidence occurred (Fig. 3 d–f), while the ridge of DHF incidence was blunt (Fig. 3 g–i). DHF incidence decreased substantially as the vaccination coverage increased at any given mosquito abundance represented by R 0 (Fig. 3 g–i). However, reduction in mosquito abundance would not necessarily decrease the incidences unanimously. In particular, at low vaccine coverage (<60%), reducing the mosquito abundance from a high level (R 0 > 15) to a moderate level (R 0 < 4) would increase the incidence, especially of DF. The maximal incidence of DHF attributable to vaccine-derived ADE was in the order of CYD20, CYD40, and CYD100 (Fig. 3 j–l). This incidence of vaccine-derived DHF for CYD100 was relatively small at a very high vaccination coverage (Fig. 3 j). In contrast, the incidence of vaccine-derived DHF for CYD40 and CYD20 was highest at 100% vaccination coverage (Fig. 3 k, l). The effect of vaccination on effective reproductive number is presented in Supplementary Appendix 4.

Fig. 3. Results from simulations plotted over mosquito abundance and vaccination coverage. Mosquito abundance is represented as basic reproductive number (R 0). Vaccination coverage is defined as V in the Methods section. (a–c) Viral inoculation rate (/1000 individuals per year), incidence (/100 000 individuals per year) of dengue fever (DF) (d–f), dengue haemorrhagic (DHF) (g–i), and DHF attributable to vaccine-derived antibody-dependent enhancement (j–l), were averaged from the last 30 years in each 150-year simulation and then averaged from 20 simulations. (a, d, g, j) CYD100, (b, e, h, k) CYD40, and (c, f, i, l) CYD20 are compared. Parameter setting for the simulations was (TFR, I, S) = (2, 0, 0·2).

Fig. 4. Incidence of dengue fever (DF), dengue haemorrhagic (DHF), and DHF attributable to vaccine-derived antibody-dependent enhancement (ADE), from simulations that assumed moderate or high mosquito abundance, plotted over vaccination coverage. Incidence (/100 000 individuals per year) of (a, b) DF, (c, d) DHF, and (e, f) DHF attributable to vaccine-derived ADE, were compared in CYD100, CYD40, and CYD20. Simulations were conducted assuming (a, c, e) moderate mosquito abundance (R 0 = 4) or (b, d, f) high mosquito abundance (R 0 = 15). Parameters were set to the same values as in Figure 3.
Preventive and predisposing effects of vaccines
Figure 3 was intersected at R 0 = 4 (moderate mosquito abundance) and R 0 = 15 (high mosquito abundance; Fig. 4). The incidence of DF responded to vaccination coverage differently between high and moderate mosquito abundances: DF incidence was more refractory to vaccination in areas of high mosquito abundance (Fig. 4 b) than in areas of moderate mosquito abundance (Fig. 4 a). The vaccines affected DHF incidence in a contrasting manner. At both high and moderate mosquito abundance, all the vaccines reduced DHF incidence (Fig. 4 c,d). Vaccine-derived DHF (Fig. 4 e,f) was much less frequent than DHF preventable by CYD100 and CYD40 (Fig. 4 c,d), while this margin was more obscure for CYD20.
Effect of inhomogeneous mixing, seasonality, and population growth
The effects of inhomogeneous mixing, seasonality, and population growth rate on the epidemiological parameters were examined at different levels of vaccination coverage (Fig. 5). It is intuitive that less inhomogeneous mixing and larger population growth were associated with increased viral inoculation rate (Fig. 5 a, c). Interestingly, stronger seasonality was correlated with slightly increased viral inoculation rate (Fig. 5 b). However, the response of disease incidence to increased viral inoculation rate was counter-intuitive. Under the situation of high mosquito abundance (R 0 = 15), the increased viral inoculation rate led to decreased DF incidence (Fig. 5 d–f), as predicted by the endemic stability hypothesis. The incidence of DHF and its relationship to vaccination coverage was affected only slightly by the variation in inhomogeneous mixing, seasonality, and population growth rate (Fig. 5 g–i).

Fig. 5. Effects of inhomogeneous mixing (I), seasonality (S), and total fertility rate (TFR) at different levels of vaccination coverage. Results from simulations are plotted over vaccination coverage and (a, d, g) inhomogeneous mixing (I), (b, e, h) seasonality (S), and (c, f, i) TFR. R 0 was set at 15. (a–c) Viral inoculation rate (/1000 individuals per year), incidence (/100 000 individuals per year) of (d–f) dengue fever (DF) and (g–i) dengue haemorrhagic (DHF) were averaged from the last 30 years in each 150-year simulation and then averaged from 20 simulations. CYD40 was used. Parameter settings were: (TFR, S) = (2, 0·2) for (a, d, g); (TFR, I) = (2, 0) for (b, e, h); (I, S) = (0, 0·2) for (c, f, i).
Temporal patterns
In Figure 6, the temporal patterns in the incidence of DF and DHF are presented for three control strategies: mosquito vector control only (Fig. 6 a), vaccination only (Fig. 6 b), and vaccination followed by vector control (Fig. 6 c). In the area of moderate mosquito abundance, all three strategies reduced the incidence of both DF and DHF (data not shown). In contrast, in an area of high mosquito abundance (R 0 = 15), mosquito control of moderate achievement (to R 0 = 4) led to an increase in incidence of DF (Fig. 6 d) and DHF (Fig. 6 g). Vaccination alone by CYD40 did not affect DF incidence markedly (Fig. 6 e), but reduced DHF incidence noticeably (Fig. 6 h). Vaccination using CYD40 followed by vector control achieved a substantial reduction in incidence of both DF (Fig. 6 f) and DHF (Fig. 6 i). Vaccination alone by CYD20 did not exert a noticeable influence on the incidence of DF (Fig. 6 j) or DHF (Fig. 6 l). However, vaccination by CYD20 which preceded vector control attenuated the potential increase in incidence that would have resulted from vector control alone for DF (cf. Fig. 6 d,k) and DHF (cf. Fig. 6 g,m).

Fig. 6. Temporal patterns in simulations employing different dengue control strategies. Incidence of dengue fever (DF) and dengue haemorrhagic (DHF) is plotted over years in simulation. The strategy was based on either (a, d, g) vector mosquito control only (b, e, h, j, l) vaccination only, or (c, f, i, k, m) vaccination followed by vector control. The temporal change in mosquito abundance (R 0) and vaccination coverage are presented in panels (a–c), while incidence (/100 000 individuals per year) is presented in (d–f, j, k) for DF and in (g–i, l, m) for DHF. CYD40 was used in (e, f, h, i) while CYD20 was used in (j–l, m). Parameters were set to the same values as in Figure 3.
DISCUSSION
Individual-based model simulation has become increasingly common for comparing disease control strategies [Reference Epstein44–Reference Morimoto and Ishikawa46]. The present study employed this methodology to predict the effects of vector control and vaccination on the incidence of dengue-related diseases.
As a result, it was predicted that mosquito control alone is likely to increase the incidence of both DF and DHF in areas of high mosquito abundance. Although extremely strong suppression of vector abundance could decrease the incidence eventually, incidence would increase transiently while mosquito reduction remains incomplete. Despite this concern, mosquito control activities will probably be continued in developing countries, partly because being endemic for dengue virus reduces the attractiveness for tourism and overseas investment. Since the vector mosquito larvae infest intended water containers as well as disposals [Reference Focks and Chadee47, Reference Manrique-Saide48], not only mosquito control but also improvement in water supply and garbage collection systems will decrease mosquito abundance [Reference Knudsen and Slooff49, Reference Reiter, Gubler, Gubler and Kuno50].
The present study emulated seroconversion rates of CYD, the dengue vaccine with the highest prospect of proceeding to phase III trial. Sensitivity analyses were conducted to compensate for the uncertainties in seroconversion rates. Consequently, the main conclusion was not affected by these uncertainties; the vaccine could attenuate the possible surge in DF and DHF driven by the decrease in mosquito abundance. However, the predisposing effect of vaccine-derived ADE would vary greatly depending on protective seroconversion rates. It should be noted that the least-favourable assumptions for a vaccine were adopted, including that vaccines always induce enhancing antibodies, the enhancing capability persists throughout life, and the vaccine does not confer cross-protection. Hence, the estimates of a predisposing effect of vaccine may be exaggerated. In addition, DHF cases caused by vaccine-derived ADE would be much fewer than DHF cases prevented by a vaccine of considerably high (although not perfect) seroconversion rates. Therefore, a vaccination programme which uses such a sub-optimal vaccine may be justifiable, at least in areas of high mosquito abundance where mosquito reduction may increase the incidence of DF and DHF. As represented by the arrows in Figure 7, the peaks of DF/DHF incidence could be circumvented if mosquito control is preceded by high vaccination coverage. Since some may feel that any vaccine that predisposes vaccinees to the risk of DHF cannot be ethically acceptable, the present study provides quantitative information to ethical and economic discussions of this issue. Although vaccination of not only small children but a large part of the population may be necessary at the initial phase of a vaccination programme [Reference Massad51], the present study did not investigate this important topic. Further studies are warranted on these issues.

Fig. 7. Optimal strategy to reduce viral inoculation rate and incidence of dengue fever (DF) and dengue haemorrhagic (DHF). The optimal strategy, which reduces the viral inoculation rate and incidence of DF and DHF, is superimposed on the results of simulations which used CYD40 (Fig. 3). This strategy, which is represented by the curved arrow in (a) and (b) is composed of a vaccination phase, and a mosquito control phase. Initially, by attaining high coverage of vaccination in ‘vaccination phase’, (a) DF incidence and (b) DHF incidence decrease. In the subsequent ‘mosquito control phase’, R 0 is reduced, thereby decreasing these incidences to a lower level. With this strategy, combining vaccination and mosquito control, the ridges of incidence of (a) DF and (b) DHF can be circumvented.
Collectively, the present study proposes a new methodology to predict and compare the population-level effect of dengue vaccines. The prediction can be updated easily as seroconversion rates are improved, or as currently unknown parameters are reported from field/experimental studies. The predictions made here, however peculiar they may appear, should be considered in developing a global dengue control strategy.
ACKNOWLEDGEMENTS
The authors thank Katia Koelle, Eiji Konishi, Bruno Guy, Paul G. Coleman, and the late Clive Davies for assistance and advice. The corresponding author would be pleased to provide technical assistance in installing, executing, and modifying the simulation software upon request.
SUPPLEMENTARY MATERIAL
For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S0950268813001866.
DECLARATION OF INTEREST
None.











