INTRODUCTION
Influenza pandemics have occurred at irregular intervals throughout human history, causing widespread morbidity and mortality. Pandemic influenza viruses are known to be re-assorted human/animal strains of the virus to which humans have little prior immunity, but the mechanisms are poorly understood that make one re-assorted strain cause a pandemic, while countless others do not ref. [Reference Nicholls1].
The paper that first claimed a connection between solar activity and influenza was published by Hope-Simpson in 1978 [Reference Hope-Simpson2]. Hope-Simpson long espoused the view that influenza is not a contagious disease, but rather associated with human responses to solar phenomenon [Reference Hope-Simpson3]. His 1978 paper purported, without any reference to literature to support the claim, that six influenza ‘pandemics’ occurred between 1918 and 1971, and the timing of each were all within ±1 year of a maximum in the sunspot cycle. However, in reality, only three pandemics are generally agreed upon to have occurred during that time period [Reference Morens and Taubenberger4–Reference Patterson13]. It is true that of these three (1918, 1957, and 1968), all in fact occurred within ±1 year of the solar cycle peaks. However, a trivial statistical analysis shows that this is not extraordinary; the Binomial 95% confidence interval for the estimated probability of observing a pandemic within ±1 year of a peak when three out of three have actually been observed is [0·29, 1·0] [Reference Clopper and Pearson14], but of all years during that time period, 16 out of 54 (30%) were within ±1 year of peak. This null hypothesis value of 30% is at the lower end of the Binomial 95% confidence interval of the observed, but within it.
However, as straightforward as this analysis is, it is based on only three events. Normally, in a paper one would never consider presenting a statistical analysis based on so few samples, because when sample sizes are very small the probability of a Type II error when testing the null hypothesis is very high [Reference Suen and Ary15], and model validation is impossible [Reference Chatfield16, Reference Casella and Berger17]. It is interesting to note that the Hope-Simpson paper was not in fact peer-reviewed, but rather correspondence to the editors of Nature. Had the paper been peer-reviewed by experts in influenza and/or statistics, it likely would have been pointed out that (a) half of the purported pandemics never actually occurred, and (b) the sample sizes were far too small for general inference.
In 1978, two astronomers, Hoyle and Wickramasinghe, espoused a theory that many diseases hitherto assumed to be infectious were actually seeded into the population from extraterrestrial origin [Reference Wickramasinghe and Wickramasinghe18]. As a ‘test’ of this theory, they attempted to explain the patterns of spread of influenza in day schools local to their university. They claimed that the only plausible explanation for the patterns they observed was that influenza was spreading in the population not via contact between people in the population, but through viruses arriving from outer space [Reference Wickramasinghe and Wickramasinghe18]. They announced their work in a paper in a news publication, New Scientist [Reference Hoyle and Wickramasinghe19], which is not peer-reviewed.
Hoyle and Wickramasinghe subsequently published a note in 1990 that claimed that the sunspot/pandemic link purported by Hope-Simpson also occurred during the ‘1978–79’ pandemic, and that their theory of extraterrestrial influenza explained this phenomenon [Reference Hoyle and Wickramasinghe20]. In reality however, the pandemic was in 1977, which was further from a solar maximum than 1978. Like the Hope-Simpson paper before it, the Hoyle and Wickramasinghe note was also a letter to the editors of Nature. Once again, had the paper been peer-reviewed by experts, it likely would have been pointed out that they got the date of the 1977 pandemic wrong, and that a statistical analysis to support their hypothesis of the purported relationships of sunspot cycles to additional pandemics prior to 1900 was entirely lacking. Indeed, it was pointed out by Lyons and Murphy in a subsequent letter to Nature that cause must necessarily precede effect, and several of the pandemics discussed by Hoyle and Wickramasinghe preceded the solar maximum [Reference Lyons and Murphy21]. They also took issue with the definition of the pandemics used, as did von Alvensleben [Reference Von Alvensleben22]. Von Alvensleben also pointed out that the pandemics listed by Hoyle and Wickramasinghe were in fact apparently randomly distributed within the periodic solar cycle.
Despite the questionable basis of these early, non peer-reviewed claims of an association between sunspots and influenza pandemics, it is now often talked about as an established ‘fact’ in the literature. Some, however, have put forward more biologically plausible explanations for the purported phenomena, including suggesting that vitamin D levels may depend on the variation in solar radiation during the sunspot cycle [Reference Hayes23], and that the migration patterns of birds that spread the influenza may be sensitive to geomagnetic changes [Reference Fuhrmann24].
Sunspot data are readily available from the Royal Observatory of Belgium in Brussels (currently available at http://www.sidc.be/silso/datafiles, accessed September 2016). Using these data, other researchers have attempted statistical analyses to verify the purported association between influenza pandemics and sunspots. This analysis examines the work of researchers that claim to verify the sunspot/pandemic effect; Ertel, Tapping et al., and Yeung [Reference Ertel25–Reference Yeung27]. Two of the analyses claim that maxima in sunspot activity are associated with influenza pandemics [Reference Tapping, Mathias and Surkan26, Reference Yeung27], while another claims that both maxima and minima in sunspot activity are associated with pandemics [Reference Ertel25]. A brief synopsis of each analysis is given below, and each is described fully in Appendix A.
Before describing each analysis, however, some things should be noted about the general problems with these analyses, primarily related to issues of robustness to analysis assumptions, and problems with data mis-transcription from sources in the literature:
-
• If an analysis used a particular formulation of a ‘distance’ statistic to assess how far a particular year lies from a maximum or minimum in sunspot activity, the conclusion of the analysis should not depend on the exact formulation of distance statistic used, when other similar and equally valid distance statistics might be employed.
-
• Identifying pandemics, particularly prior to the 19th century, is a highly subjective process, and there is disagreement in the literature on the list of pandemics prior to the early 1800s. Analyses of the potential of a connection between sunspot number and influenza activity should be robust when using different, equally plausible lists of pandemics.
-
• Similarly, when using multiple citations to sources of lists of pandemic years, the analysis may involve assessing pandemic years by only taking years for which k out of the n sources agree; in which case, the analysis conclusions should be robust to different assumptions of k.
-
• There are two alternate specifications of sunspot activity, the Wolf (or ‘Zürich’, or ‘International’) and Group sunspot numbers; it has been noted in the literature that the latter is likely more accurate prior to the modern era, while the former is more accurate for characterising recent ongoing levels of sunspot activity [Reference Hoyt and Schatten28–Reference Clette, Balogh, Hudson, Petrovay and von Steiger31]. Ertel, Tapping et al., and Yeung [Reference Ertel25–Reference Yeung27] all used the Wolf sunspot numbers, even though for the two latter analyses the Group sunspot numbers were also available. Analysis conclusions should be robust to different specifications of the sunspot activity.
-
• In general, analysis conclusions should be robust to changes in any of the arbitrary selections used in the analysis.
-
• Analyses should also be robust under alternate choices of the statistical analysis methodology used, particularly when a particular analysis method makes maximal use of the information in the data. Thus, an analysis that simply compared something like the mean of a ‘distance’ statistic for pandemic years to the average distance statistic for all years should be robust if a more powerful, non-parametric statistical test, such as the Kolmogorov–Smirnov or Anderson–Darling tests [Reference Richardson32], is used to compare the shape of the two distributions from which the means are calculated. Two distributions, for instance, can have similar means, but very different shapes. And, particularly for small samples, one outlier in a distribution of just a few events may dramatically effect the mean, yet overall the distribution is consistent with being drawn from the larger distribution.
-
• Many of the different compilations of lists of past pandemics were actually derivative of the same historical sources. This is noted in Yeung [Reference Yeung27], for example. The various references also cited each other frequently. Thus, lists of pandemics presented in the literature as being independent compilations, were not.
-
• Note here that the Ertel, Tapping et al., and Yeung [Reference Ertel25–Reference Yeung27] analyses all made transcription mistakes in the dates of influenza pandemics cited from the literature.
The following sections give brief synopses of the Ertel, Tapping et al., and Yeung [Reference Ertel25–Reference Yeung27] analyses, followed by a presentation of our own analysis of the available data. The robustness of the analysis to the assumption of various different, yet equally valid, ‘distance’ statistics, was assessed. For completeness, the analysis was performed using 10 different compiled lists of purported pandemics between 1700 and 1977, and also subsets of purported pandemics mutually agreed upon by k (where k goes from 1 to 10) of the reviews in refs [Reference Morens and Taubenberger4–Reference Patterson13]Footnote 1 (all of which were published after the 1977 pandemic, and cover the period from 1700 onwards). The pandemic year 2009 was added to the lists. Additionally, the robustness of the analysis to using the Wolf and Group sunspot numbers was assessed.
No statistically significant evidence that solar activity is related to influenza activity was found.
Ertel [Reference Ertel25] analysis
In 1994, Ertel, a parapsychologist, performed an analysis claiming to verify that influenza pandemics occurred near both sunspot minima and maxima. He also published a later analysis claiming a link between sunspots and human creativity [Reference Ertel and Nyborg36].
Using lists of influenza epidemics (many of which were not pandemics) between 1700 and 1985 from nine different sources in the literature [Reference Hope-Simpson2, Reference Pyle12, Reference Patterson13, Reference Hoyle and Wickramasinghe19, Reference Creighton33, Reference Assaad, Bektimirov, Ljungars-Esteves and Stuart-Harris37–Reference Burnet40] and an encyclopaedia entry from 1970, Ertel arbitrarily defined a ‘pandemic’ to be an epidemic that at least three of the sources agreed upon. Ertel included in these sources several cited sources that were actually derivative of other cited sources (thus the 10 sources were not independent). Ertel also mis-transcribed data from several sources, and used some older references even when more up to date reviews were made available by some authors (for instance the list of epidemics in Beveridge et al. [Reference Beveridge38] was updated in Beveridge [Reference Beveridge10]).
To determine whether or not epidemics appeared to be clustered around the times of maxima and minima in sunspot activity, Ertel defined a metric based on the unsigned distance, D, in years of an epidemic from a sunspot maximum. He then transformed D into a new statistic, Q, which was −1 if D was the maximal possible distance between sunspot maxima, or +1 if it was at the minimum possible distance:
where D max is the maximum value of D during a solar cycle (where each solar cycle begins at the solar minimum).
While this statistic might, on the face of it, seem reasonable, it lacks sensitivity to whether or not an event occurs near a solar cycle minimum (the solar cycle is highly asymmetric in its periodicity, with maxima often occurring just a few years after a minimum, thus midway between two maxima usually does not correspond to the minimum, and the minimum in Q also thus does not generally correspond to the minimum in the solar cycle). Additionally, the Q statistic is not sensitive to whether the epidemic comes before or after the sunspot peak, and has only limited sensitivity to whether the epidemic is near a minimum in sunspot activity, despite the fact that Ertel was attempting to show that influenza epidemics occur near both maxima and minima in sunspot activity.
Cross-checking the analysis, as described in Appendix A, revealed that the results are highly sensitive to Ertel's choice of distance statistic and statistical analysis methodology. Correcting Ertel's mis-transcription of the data, and removing derivative lists of epidemics also negate Ertel's claims of significance.
Thus, largely because of the choice of distance measure and mis-transcriptions of data, Ertel concludes that sunspot activity is significantly associated with influenza activity.
In addition to these problems with the analysis, Ertel concluded that during the 1700s the influenza pandemics appeared to significantly occur around the sunspot minima, but after that there was no significant clustering. Ertel came up with an explanation for the decrease in significance by stating that it must have something to do with long-term changes in sunspot activity. This is an excellent example of ‘cherry-picking’ data, where it is claimed that the results testing the null hypothesis are significant… except where they aren't [Reference Dienes41, Reference Morse42].
Tapping et al. [Reference Tapping, Mathias and Surkan26] analysis
Tapping et al. [Reference Tapping, Mathias and Surkan26] performed an analysis where they examined the distance, in years, of influenza pandemics to the nearest sunspot maximum. The sunspot cycle periodicity is not constant and has varied since 1700 between 9 and 14 years. Tapping et al. [Reference Tapping, Mathias and Surkan26] thus expressed the distance of pandemics to sunspot maxima as fractions of the period of the sunspot cycle at that point in time (i.e. as a phase), defined as
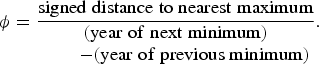 $$\phi = \displaystyle{{{\rm signed}\;{\rm distance}\;{\rm to}\;{\rm nearest}\;{\rm maximum}} \over \matrix{({\rm year}\;{\rm of}\;{\rm next}\;{\rm minimum}) \cr\qquad- ({\rm year}\;{\rm of}\;{\rm previous}\;{\rm minimum})} }.$$
$$\phi = \displaystyle{{{\rm signed}\;{\rm distance}\;{\rm to}\;{\rm nearest}\;{\rm maximum}} \over \matrix{({\rm year}\;{\rm of}\;{\rm next}\;{\rm minimum}) \cr\qquad- ({\rm year}\;{\rm of}\;{\rm previous}\;{\rm minimum})} }.$$
Using this metric, they attempted to determine if maxima in solar activity have been associated with subsequent increased incidence of influenza pandemics.
As described in Appendix A, the analysis of the data in the Tapping et al. [Reference Tapping, Mathias and Surkan26] paper appears to have multiple issues, and their analysis results were not reproducible.
Yeung [Reference Yeung27] analysis
Yeung [Reference Yeung27] performed an analysis using Binomial confidence intervals to examine the statistical significance of the fraction of influenza pandemics occurring during years where the average number of sunspots was above the 60th percentile. The analysis was published in the journal Medical Hypotheses, which at the time was not peer-reviewed.
As described in Appendix A, there were several apparent typos or errors in the paper, and the results of the analysis were not robust to changes in the arbitrary cutoff in sunspot number. Indeed, the rather unusual choice of using the 60th percentile as a cutoff (rather than more obvious choices like perhaps the median, or the 10th or 90th percentiles) happens to have been in a relatively narrow range of selection values that ensured the best apparent statistical significance.
THIS ANALYSIS
Data
This analysis examined the data collected by several reviews of influenza pandemics from 1700 to 1977 [Reference Morens and Taubenberger4–Reference Patterson13], and added to these data the pandemic year of 2009. It should be noted that some of the reviewers listed only pandemics, while others listed both ‘serious’ outbreaks and pandemics. For consistency of comparison, of the latter only the ones designated by the reviewer as pandemics are tabulated. Table 1 summarizes the data for outbreaks labelled as pandemics. As noted in Table 1, many of the cited references have cited references in common (and indeed, cite each other). However, while the data are highly derivative, none of the lists are completely identical.
Table 1. Summary of influenza outbreaks from 1700 to 1977 labelled as pandemics, listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [Reference Morens and Taubenberger4–Reference Patterson13]. The pandemic year of 2009 was also included in the data

3 Cites [Reference Pyle12, Reference Creighton33–Reference Hirsch35, Reference Finkler and Stedman43]. Has 1733 not 1732.
4 Cites [Reference Pyle12, Reference Patterson13, Reference Creighton33–Reference Hirsch35, Reference Beveridge38, Reference Finkler and Stedman43, Reference Vaughan44].
5 Cites [Reference Potter, Nicholson, Webster and Hay8, Reference Beveridge10, Reference Pyle12, Reference Patterson13, Reference Thompson and Thompson34, Reference Hirsch35, Reference Beveridge38, Reference Finkler and Stedman43, Reference Vaughan44].
6 Cites [Reference Potter, Nicholson, Webster and Hay8, Reference Beveridge10, Reference Patterson13].
7 Cites [Reference Beveridge10, Reference Pyle12, Reference Patterson13, Reference Creighton33–Reference Hirsch35, Reference Beveridge38, Reference Finkler and Stedman43]. Has 1799 not 1800.
8 Cites [Reference Patterson13, Reference Beveridge38, Reference Burnet45].
9 Cites [Reference Pyle12, Reference Patterson13, Reference Creighton33–Reference Hirsch35, Reference Finkler and Stedman43, Reference Vaughan44].
10 Cites [Reference Creighton33, Reference Hirsch35, Reference Thompson46]. Has 1782 not 1781.
Figure 1 shows the annual time series of Wolf and Group sunspot numbers by year [Reference Hoyt and Schatten28–Reference Clette, Balogh, Hudson, Petrovay and von Steiger31] (available from the Royal Observatory of Belgium in Brussels, at http://www.sidc.be/silso/datafiles, accessed September 2016), with pandemic years indicated and coloured by number of reviewers agreeing that a pandemic occurred each particular year. For the period from 1995 onwards, the Group sunspot numbers are assumed to be the same as the Wolf numbers.

Fig. 1. Wolf and Group sunspots by year from 1700 to 2014. Overlaid is the timing of purported pandemics, as listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [Reference Morens and Taubenberger4–Reference Patterson13], with the points coloured and sized relative to the number of reviewers agreeing on the date.
Analysis methods
For thoroughness, the data were analysed using several methods that have been used in the past. For all analysis methods, the results were examined for lists of pandemics agreed upon by at least k of the 10 reviews in Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [Reference Morens and Taubenberger4–Reference Patterson13], where k goes from 1 to 10.
All analyses were repeated using the Wolf and Group sunspot numbers.
To begin, the fraction of pandemic years that came within ±1 year of maxima in sunspot activity were compared with the fraction for all years between 1700 and 2014. This was also done for the fraction of pandemic years that came within ±1 year of minima in sunspot activity, and also for either maxima or minima.
For pandemic years, the distribution of a temporal distance statistic for pandemic years to the nearest year of sunspot maxima was compared with the distribution for all years between 1700 and 2014. Two different statistics were explored:
-
1. The Q statistic used in the Ertel analysis [Reference Ertel25], shown in Equation (1).
-
2. The ϕ statistic used in the Tapping et al. analysis [Reference Tapping, Mathias and Surkan26], shown in Equation (2).
Finally, the distribution of sunspot numbers for pandemic years was compared with the distribution for all years, similar to the analysis of Yeung [Reference Yeung27].
Statistical methods
The analysis of potential relationships between the timing of pandemic influenza epidemics and sunspot cycles presents several difficulties that appear to be under-appreciated in the literature.
To begin with, the analysis inherently involves small sample sizes. Influenza pandemics are relatively rare, and less than two dozen pandemics between 1700 and 2009 have been purported. In this analysis, when comparing the observed number, k, of n pandemics satisfying some selection criteria (like being within ±1 year of a solar sunspot maximum, for instance) to the expected fraction, p, the Binomial probability was assessed of observing by mere random chance at least k out of n, given p.
In many cases, one wishes to assess whether or not two distributions appear to be drawn from the same underlying distribution, such as the distribution of a metric that assesses the temporal ‘distance’ between a pandemic year to the nearest year of a sunspot maximum or minimum. Any binning of data to try to compare distributions necessitates loss of information [Reference Pyle48, Reference Williams49], thus in this analysis, the non-parametric two-sample Kolmogorov–Smirnov test [Reference Pettitt and Stephens50], and Anderson–Darling test [Reference Scholz and Stephens51] are applied to compare the shapes of two distributions. The K–S and A–D tests do not require arbitrary binning of the data, and thus are more statistically powerful than binned methods of distribution comparison. The K–S and A–D tests are similar, but the formulation of the K–S statistic tends to be more sensitive to differences in the central portion of distributions, whereas the A–D statistic tends to be more sensitive to differences in the tails [Reference Scholz and Stephens51].
However, the standard P-values assessing the significance of these test statistics are only reliable for continuous data [Reference Pettitt and Stephens50]. The data were necessarily binned in integer years, rather than being continuous in time, thus any distance statistic to sunspot activity extrema derived from these data will also not be continuous, but rather have a set of discrete values. Thus bootstrapping procedure was applied to assess the significance of the K–S and A–D statistics [Reference Romano52, Reference Præstgaard53] when the data are discrete. If the first sample is much larger than the second, each of sizes M and N, respectively, One thousand samples of size N were bootstrapped from the first sample, and the K–S and A–D statistics comparing the first sample to the bootstrapped sample were calculated. The distribution of these test statistics formed the probability distribution of the test statistic under the null hypothesis that the second sample was drawn from the same distribution as the first. This probability distribution was then used to assess the P-value of obtaining a value at least as large as some observed value of the K–S (or A–D) statistic (larger values of the statistic indicated distributions that were more different).
The sunspot activity data were continuous, thus to compare the distribution of sunspot activity of pandemic years to the distribution for all years, the standard P-value assessments of the K–S and A–D tests were employed.
The analysis was conducted in the R statistical programming language, version 3.3.2 [54]. The R code and data associated with the analysis can be found at https://github.com/smtowers/sunspots_and_pandemics_analysis.
Results
The results of the analysis of pandemics listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [Reference Morens and Taubenberger4–Reference Patterson13], and assessed using the Wolf and Group sunspot numbers, are shown in Fig. 2.

Fig. 2. The results of the analyses of pandemic data as listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [Reference Morens and Taubenberger4–Reference Patterson13], assessed using the Wolf and Group sunspot numbers (top row and bottom row of plots, respectively). The plots show the P-values assessed by the analyses, vs. the minimum number of reviewers agreeing that an outbreak or pandemic occurred. The first plot in the top and bottom rows shows the Binomial probability of the observed fraction of outbreak years within ±1 year of a maximum in sunspot activity, given the expected fraction for all years (and similarly for the years within ±1 year of an extremum in sunspot activity). The plots in the second, third, and fourth columns, respectively, show the re-creation of the Ertel, Tapping et al., and Yeung analyses [Reference Ertel25–Reference Yeung27], respectively, with the use of the Kolmogorov–Smirnov and Anderson–Darling tests to assess significance.
In all cases, and for all methodologies used, no significant association was found between sunspot number and pandemic timing.
SUMMARY
This analysis examined several past analyses that purported to show a statistically significant connection between sunspot activity and the timing of influenza pandemics. In all cases, the analyses either had mis-transcriptions of the dates of influenza pandemics listed in the literature, and/or made mistakes in the statistical analyses, and/or the analyses were not robust to arbitrary assumptions made to select the data, or the metrics used to assess the relationship between sunspot activity and the timing of influenza pandemics. In all cases, correcting these issues resulted in concluding that no significant relationship is apparent.
It is notable that in recent years other analyses have claimed that sunspot cycles influence everything from breast cancer incidence, to hip fractures, blood pressure changes, cardiac problems, plague, and cholera [Reference Caniggia and Scala55–Reference Burns58]. In addition to general poor statistical methodology, the problem with many such analyses is that some researchers search among a wide array of datasets for apparent statistically significant effects, publishing when they finally find them; a practice pejoratively known as ‘P-value fishing’ or ‘significance fishing’ [Reference Figdor59]. By mere random chance, on average 5% of the time if one fishes among enough datasets, one will reject the null hypothesis with α = 0·05, even though the null hypothesis is actually true.Footnote 2
The analyses presented here are thus merely exemplars of wider problems, and reviewers can benefit from being aware of these issues.
APPENDIX A
INTRODUCTION
The following sections examine in detail the analyses of Ertel, Tapping et al., and Yeung [Reference Ertel25–Reference Yeung27]. Each of the analyses used different methodologies, and each purported to find statistically significant evidence that sunspot activity is related to the timing of influenza pandemics.
As will be described below, amongst other issues, all three analyses made mistakes in transcription of lists of pandemic years from the literature and/or in their calculations. All of the analyses were not robust to changes in the arbitrary assumptions made.
For reference when discussing these analysis, the data collected by several reviews of influenza pandemics from 1700 to 1977 have been compiled [Reference Morens and Taubenberger4–Reference Patterson13]. Subsets of these reviews (plus reviews that were entirely derivative of these) were used by the Ertel, Tapping et al., and Yeung [Reference Ertel25–Reference Yeung27] analyses. Table 2 summarizes the data for outbreaks labelled as pandemics.
Table 2. Summary of influenza pandemics from 1700 to 1977, listed by Morens and Taubenberger, Mamelund, Lattanzi, Hampson and Mackenzie, Potter, Garrett, Beveridge, Kilbourne, Pyle, and Patterson [Reference Morens and Taubenberger4–Reference Patterson13]. In this analysis, the pandemic year of 2009 is also included in the data

It should be noted that some of the reviewers in Table 2 listed only pandemics, while others listed both ‘serious’ outbreaks and pandemics. For consistency of comparison from reviewer to reviewer, of the latter only the ones designated by the reviewers as pandemics were tabulated. As noted in Table 2, many of the cited references have cited references in common (and indeed, cite each other). However, while the data are highly derivative, none of the lists are completely identical.
ERTEL [Reference Ertel25] ANALYSIS
Overview
In 1994, Ertel, a parapsychologist, performed an analysis claiming to verify that influenza epidemics occurred near the times of both sunspot minima and maxima [Reference Ertel25]. He also published a later analysis claiming a link between sunspots and human creativity [Reference Ertel and Nyborg36].
Using the Wolf sunspot numbers, and lists of influenza epidemics (not pandemics) between 1700 and 1985 from 10 different sources in the literature [Reference Hope-Simpson2, Reference Pyle12, Reference Patterson13, Reference Hoyle and Wickramasinghe20, Reference Creighton33, Reference Assaad, Bektimirov, Ljungars-Esteves and Stuart-Harris37–Reference Silverstein39, 62, Reference Tschijewsky63], Ertel arbitrarily defined a ‘pandemic’ to be an epidemic that at least three of the 10 sources agreed upon. The data, as presented in Ertel [Reference Ertel25], are shown in Table 3.
Table 3. Re-creation of Table 1 of Ertel [Reference Ertel25]. The data were taken from Assaad, Beveridge et al., Hoyle, Collier's Encyclopedia, Creighton, Hope-Simpson, Patterson, Pyle, Silverstein, and Tschijewsky [Reference Hope-Simpson2, Reference Pyle12, Reference Patterson13, Reference Hoyle and Wickramasinghe20, Reference Creighton33, Reference Assaad, Bektimirov, Ljungars-Esteves and Stuart-Harris37–Reference Silverstein39, 62, Reference Tschijewsky63]. The */** before/after a year indicates years that Ertel [Reference Ertel25] identified to be within ±1 year of a minimum/maximum in solar activity. However, note that there are several errors in the data transcription from the sources (see text for details), and several sources list both pandemics and outbreaks, not just pandemics. Correctly transcribed data for pandemics only are shown in Table 2

To determine whether or not epidemics appeared to be clustered around the times of maxima in sunspot activity, Ertel defined a metric based on the unsigned distance, D, in years of a pandemic from a maximum in sunspot activity. He then transformed D into a new statistic, Q, which was −1 if D was the maximal possible distance between sunspot activity maxima, or +1 if it was at the minimum possible distance:
where D max is the maximum value of D during a solar cycle (where each solar cycle begins at a minimum in sunspot activity). While this statistic might, on the face of it, seem somewhat reasonable, it lacks sensitivity to whether or not an event occurs near a solar cycle minimum (the solar cycle is highly asymmetric in its periodicity, with maxima often occurring just a few years after a minimum, thus midway between two maxima usually does not correspond to the minimum, and the minimum in Q also thus does not generally correspond to the minimum in the solar cycle). The resulting statistic used in Ertel [Reference Ertel25] thus was not sensitive to whether the pandemic came before or after the sunspot peak, and had only limited sensitivity to whether the pandemic was near a minimum in sunspot activity. This, despite the fact that the analysis was attempting to show that influenza pandemics occurred near both maxima and minima in sunspot activity.
Ertel took the average value of Q,
![]() ${\bar {\!Q}}$
, for all pandemic years, and then used bootstrap methods to assess the probability of observing at least that value of
${\bar {\!Q}}$
, for all pandemic years, and then used bootstrap methods to assess the probability of observing at least that value of
![]() ${\bar {\!Q}}$
(note that a high value of
${\bar {\!Q}}$
(note that a high value of
![]() ${\bar {\!Q}}$
would indicate that pandemics were more likely to occur close to times of maxima in solar activity).
${\bar {\!Q}}$
would indicate that pandemics were more likely to occur close to times of maxima in solar activity).
Re-creation of the analysis, as presented in the paper
In the caption of Table 1 in his paper, Ertel made the comment that he believed the fraction of the 286 years between 1700 and 1985 between ±1 year of a maximum or minimum in sunspot activity was 0·357 (i.e. he claimed 102 years were within 1 year of an extrema in activity). However, there were 51 extrema in sunspot activity during that period, thus the total number of years within ±1 year of an extrema in activity was 154 (1985 was 1 year before a minimum in solar activity in 1986), yielding an actual fraction of 0·538.
Note that Ertel mistakenly identified the year 1803 as not being close to an extrema in sunspot activity, but in reality it was within 1 year of a maxima. There were several errors in the data Ertel presents in the paper, as described below. However, taking the pandemic years presented in the paper at face value, 21 out of the 25 years were within 1 year of an extrema in sunspot activity, in agreement with the result quoted in the paper. The resulting average value of Q was
![]() ${\bar {\!Q}} = 0 \!\cdot \!225$
, in slight disagreement with the value presented in the paper of
${\bar {\!Q}} = 0 \!\cdot \!225$
, in slight disagreement with the value presented in the paper of
![]() ${\bar {\!Q}} = 0 \! \cdot \!24$
. Additionally this analysis found, using Ertel's bootstrapping method, that the probability of observing
${\bar {\!Q}} = 0 \! \cdot \!24$
. Additionally this analysis found, using Ertel's bootstrapping method, that the probability of observing
![]() ${\bar {\!Q}} \ge 0 \! \cdot \!225$
by mere random chance was P = 0·02, which is less impressive in its significance than the P = 0·005 quoted in the paper.
${\bar {\!Q}} \ge 0 \! \cdot \!225$
by mere random chance was P = 0·02, which is less impressive in its significance than the P = 0·005 quoted in the paper.
In addition, rather than just examining the mean of Q (which is based on a small sample size in this case), there are more statistically powerful non-parametric statistical tests, such as the Kolmogorov–Smirnov (K–S) and Anderson–Darling (A–D) tests [Reference Richardson32, Reference Pettitt and Stephens50, Reference Scholz and Stephens51], that compare two distributions and calculate the probability of observing the two, under the null hypothesis that the two samples were drawn from the same distribution. The K–S and A–D tests are similar, but the formulation of the K–S statistic tends to be more sensitive to differences in the central portion of distributions, whereas the A–D statistic tends to be more sensitive to differences in the tails [Reference Scholz and Stephens51]. When the K–S test was applied, comparing the Q of the pandemic years listed in Ertel [Reference Ertel25] to the value of Q for all years between 1700 and 1985, a P-value of P = 0·10 was obtained. Applying the A–D test yielded a P-value of P = 0·09.
Thus, even with the erroneous data used as the basis for the original analysis, the claims of significance were not upheld when more statistically powerful tests of significance were used.
Corrections to the data
The author was able to locate and examine eight of the 10 references used in Ertel [Reference Ertel25]. Of these eight, several were highly, or completely, derivative. For instance, Ertel's reference (12) was a paper by Assaad et al. [Reference Assaad, Bektimirov, Ljungars-Esteves and Stuart-Harris37] that cited Ertel's reference (7), Beveridge et al. [Reference Beveridge38]. In fact, the pandemics listed by Assaad et al. [Reference Assaad, Bektimirov, Ljungars-Esteves and Stuart-Harris37] were identical to the ‘probable’ pandemics listed by Beveridge et al. [Reference Beveridge38]. This was thus not an independent reference. Similarly, reference (15) in Ertel [Reference Ertel25] was a book by Silverstein [Reference Silverstein39] that cited Beveridge et al. [Reference Beveridge38] as a reference, and the years listed by Silverstein in Table 1 of Ertel [25] were identical to the years listed by Beveridge et al. [Reference Beveridge38], thus this was also not an independent reference.
Ertel [Reference Ertel25] listed the years indicated by Beveridge et al. [Reference Beveridge38] to be ‘possible’ or ‘probable’ pandemics, but inexplicably left out the years 1729, 1732, 1742, 1900, 1918, 1946, 1957, 1968, and 1977 listed by Beveridge et al. [Reference Beveridge38], and added the year 1800, which was actually noted to be 1802 in Beveridge et al. [Reference Beveridge38]. In the derivative Assaad et al. [Reference Assaad, Bektimirov, Ljungars-Esteves and Stuart-Harris37] data, Ertel included the ‘probable’ pandemic years listed by Beveridge et al. [Reference Beveridge38], but mis-transcribed 1977 as 1979.
Reference (6) in Ertel [Reference Ertel25] was the paper by Hope-Simpson [Reference Hope-Simpson2]; Ertel [Reference Ertel25] mis-transcribed the 1977 pandemic year noted by Hope-Simpson as 1978. The Hope-Simpson paper additionally only listed pandemics from 1918 on wards. For proper assessment of source agreement on epidemic years, the sources should cover the same time period, and also use similar criteria in selecting ‘pandemic’ years. In the case of the data presented by Ertel [Reference Ertel25], some of the sources listed epidemic years, and others, like Hope-Simpson [2], only listed pandemic years.
Reference (14) in Ertel [Reference Ertel25] was a reference to the 1970 version of Collier's Encyclopedia, which the author could also not locate. Referencing encyclopaedic entries rather than the references cited within is a questionable, and the outbreak years listed in Collier's were certainly derivative of the other sources listed by Ertel [Reference Ertel25].
Reference (16) in Ertel [Reference Ertel25] was a paper the author could not locate, by Tschijewsky [Reference Tschijewsky63]. However, note the epidemics listed by Tschijewsky [Reference Tschijewsky63] were virtually identical to those listed by Creighton [Reference Creighton33], which was Reference (10) in Ertel [Reference Ertel25], with the addition of 1918.
Removed from consideration in the analysis were thus Assaad (identical to Beveridge et al. [Reference Beveridge38]), Creighton [Reference Creighton33] (later sources either cited Creighton, or cited sources that cited Creighton), Silverstein (derived from Beveridge and Beveridge et al. [Reference Beveridge10, Reference Beveridge38]), Tschijewsky (derived from Creighton), and the reference to Collier's Encyclopedia.
Ertel [Reference Ertel25] also used some older references, even though more up to date reviews by some authors were available in at the time he wrote his paper (for instance, the 1977 list of pandemics in ref. [Reference Beveridge38] was updated in 1991 in [Reference Beveridge10], and the 1971 list in ref. [Reference Burnet40] was updated in 1979 in [Reference Burnet45]).
The correct data, for pandemics only (not an arbitrary mixture of epidemics and pandemics, as listed by Ertel) are included in the data sources shown in Table 2.
Use of corrected data, alternate sunspot number compilations, and alternate distance statistics
As described in the main text of this paper, the corrected data in Table 2 did not yield statistically significant evidence of a relationship between sunspot activity and the timing of pandemics, for either Ertel's Q statistic, or other equally valid analysis methods, and when using either the Wolf or Group sunspot numbers.
Summary
The data in Ertel [Reference Ertel25] had many mis-transcriptions from the literature, and included a mixture of lists of influenza pandemics and outbreaks, even though the paper purported to examine only pandemics. However, taking the data in Ertel [Reference Ertel25] as originally presented, this analysis largely verified the results presented in the paper, except the P-value was P = 0·02, not P = 0·005 as claimed, but the more powerful non-parametric K–S and A–D tests found no statistically significant difference between the distribution of Q for pandemic years compared with other years.
When the mis-transcribed data in Ertel [Reference Ertel25] were corrected and several derivative sources were removed, this analysis found no statistically significant difference between the distribution of Q for pandemic years compared with other years.
TAPPING ET AL. [Reference Tapping, Mathias and Surkan26] ANALYSIS
Tapping et al. [Reference Tapping, Mathias and Surkan26] performed an analysis where they examined the distance, in years, of influenza pandemics to the nearest sunspot maximum. The sunspot cycle periodicity is not constant and has varied since 1700 between 9 and 14 years. Tapping et al. [Reference Tapping, Mathias and Surkan26] thus express the distance of pandemics to sunspot maxima as fractions of the period of the sunspot cycle at that point in time (i.e.; as a phase). Explicitly, they define this as
 $$\phi = \displaystyle{{{\rm signed}\;{\rm distance}\;{\rm to}\;{\rm nearest}\;{\rm maximum}} \over\matrix {({\rm year}\;{\rm of}\;{\rm next}\;{\rm minimum})\,- \cr\qquad ({\rm year}\;{\rm of}\;{\rm previous}\;{\rm minimum})}}$$
$$\phi = \displaystyle{{{\rm signed}\;{\rm distance}\;{\rm to}\;{\rm nearest}\;{\rm maximum}} \over\matrix {({\rm year}\;{\rm of}\;{\rm next}\;{\rm minimum})\,- \cr\qquad ({\rm year}\;{\rm of}\;{\rm previous}\;{\rm minimum})}}$$
Using this metric, they attempted to determine if maxima in solar activity have been associated with subsequent increased incidence of influenza pandemics.
They binned these phases into five equally sized bins between –0·5 and +0·5. Note, however, that |ϕ| can be greater than 0·5 because a maximum in sunspot activity does not, in general, fall equidistant between two minima in sunspot activity. In fact, since 1700 the average duration between a minimum in sunspot activity to the next maximum is generally around 2 years shorter than the average duration between a maximum and the next minimum. Because of this, not only can |ϕ| > 0.5, but also ϕ is not uniformly distributed. Tapping et al. [Reference Tapping, Mathias and Surkan26] did not mention that they were aware of this, and indeed, in their analysis, they assumed that ϕ should be uniformly distributed between –0·5 and +0·5. For the pandemic years that they examined, it happens that |ϕ| < 0.5 for all of them. They did not show the distribution of ϕ for non-pandemic years.
Using a Monte Carlo method that assumed these fractions were continuously and uniformly distributed between −0·5 and 0·5 (they were not), they then assessed the probability of observing the number of events in the two bins between −0·1 and +0·3, and concluded that significant effects were evident.
Re-creation of the analysis, as presented in the paper
The data in the Tapping et al. [Reference Tapping, Mathias and Surkan26] were derived from Garrett and Potter [Reference Potter, Nicholson, Webster and Hay8, Reference Garrett9]. However, even though Tapping et al. [Reference Tapping, Mathias and Surkan26] ostensibly examined only pandemics in their analysis, they included several years from both sources of data that were clearly labelled by the authors as not being apparent pandemics.
The data given in the Tapping et al. [Reference Tapping, Mathias and Surkan26] paper are shown in Table 4. Shown in red are the years incorrectly transcribed as being listed as pandemics by the sources. In addition, Tapping et al. [Reference Tapping, Mathias and Surkan26] make several apparent mistakes in their calculation of ϕ, as noted in Table 4. Note that these mistakes were apparently carried over into their histograms of the data shown in their paper.
Table 4. Re-creation of Table 1 in Tapping et al. [Reference Tapping, Mathias and Surkan26], showing the years they considered as pandemic years in their analysis. In several cases, shown in blue, outbreaks clearly designated by the source as not being a pandemic year were included in the data. In addition, in the several instances indicated in red, the phase, ϕ, was incorrectly calculated

Using the correctly calculated phases, this analysis was unable to reproduce the results of the Tapping et al. [Reference Tapping, Mathias and Surkan26] paper.
Use of corrected data, alternate sunspot number compilations, and alternate distance statistics
As described in the main text of this paper, the corrected data in Table 2 did not yield statistically significant evidence of a relationship between sunspot activity and the timing of pandemics, for either the ϕ statistic used by Tapping et al. [Reference Tapping, Mathias and Surkan26], or other equally valid analysis methods, and when using either the Wolf or Group sunspot numbers.
Summary
Unfortunately, the data, as presented in the Tapping et al. [Reference Tapping, Mathias and Surkan26] paper, had multiple apparent errors in their calculation of their ϕ statistic, and they included several years in their analysis that were not listed as pandemic years by the sources.
When corrected data were used, as presented in Table 2, no statistically significant evidence of a relationship between sunspot activity and the timing of influenza pandemics was found.
YEUNG [Reference Yeung27] ANALYSIS
Yeung [Reference Yeung27] performed an analysis using Binomial confidence intervals to examine the statistical significance of the fraction of influenza pandemics occurring during years where the average number of sunspots is above the 60th percentile [Reference Yeung27]. The analysis was published in the journal Medical Hypotheses, which at the time was not peer-reviewed.
This analysis is recreated below, and it is shown that there were several apparent typos or errors in the paper, and the results of the analysis were not robust to changes in the arbitrary cutoff in sunspot number, SSN. Indeed, the rather unusual choice of using the 60th percentile as a cutoff (rather than more obvious choices like perhaps the median, or the 10th or 90th percentiles) happens to have been in a relatively narrow range of selection values that ensured the best apparent statistical significance.
Again, as discussed below, to maximize the power of the analysis, the analysis of Yeung was refined to use un-binned methods, and no statistically significant evidence was found that sunspot number impacted the timing of influenza pandemics.
Re-creation of the analysis, as presented in the paper
The data used in the Yeung [Reference Yeung27] analysis are shown in Table 5. Indicated in red in the table are data that were mis-transcribed from the original sources.
Table 5. Re-creation of Table 1 in Yeung [Reference Yeung27], showing the years Yeung considered as pandemic years in the analysis. In several cases, indicated in red, the data are mis-transcribed from the original sources

Oddly, although Yeung [Reference Yeung27] listed pandemics noted by five reviewers [Reference Potter, Nicholson, Webster and Hay8, Reference Beveridge10, Reference Kilbourne11, Reference Pyle12, Reference Patterson13, Reference Beveridge38], in the analysis he excluded the data from [Reference Patterson13] without explanation.
The outbreaks agreed upon by Beveridge and Beveridge et al. [Reference Beveridge10, Reference Beveridge38], Pyle [Reference Pyle12], Kilbourne [Reference Kilbourne11], and Potter [Reference Potter, Nicholson, Webster and Hay8] were, according to Yeung [Reference Yeung27], 1729, 1781, 1830, 1889, 1918, 1957, and 1968. In reality, however, Pyle [Reference Pyle12] did not list 1729 as a pandemic year, but rather 1732, and Kilbourne [Reference Kilbourne11] listed 1833 as a pandemic year, not 1830. However, when the 7 years as presented were considered, 6 did indeed have a Wolf sunspot number greater than the arbitrary cut-off of 50, which was the upper 60th percentile, which yielded a P-value of P = 0·019, as presented in the paper.
However, SSN ⩾ 50 was the 60th percentile, which seems a somewhat odd choice. As shown in Fig. 3, it turns out that the choice of the 60th percentile as a cutoff yielded an almost maximal apparent significance in the result. Using a more standard percentile in the analysis, like the median, or 90th percentile, did not yield significant results. In addition, the use of the Group sunspot numbers in lieu of the Wolf sunspot numbers did not yield a significant result for any cutoff.

Fig. 3. Apparent significance of the results of the Yeung [Reference Yeung27] analysis, as a function of the percentile value used to assess the cutoff in sunspot number, SSN. The result of Yeung [Reference Yeung27] was obtained with an SSN percentile cutoff of 60% (0·6), which resulted in almost maximal apparent significance. Note that the Group sunspot numbers do not yield a significant result for any percentile used to assess the cutoff in SSN.
Summary
The Yeung [Reference Yeung27] analysis made several mis-transcriptions of lists of pandemics in the literature, and arbitrarily chose to exclude one of the lists without explanation. Further, one of the selections used in the analysis was unusual in its choice, and was in a narrow range of values that achieved the best apparent significance; changing the selection to more standard values negated the claims of significance.
As noted in the text of the main paper, when corrected lists of pandemic years were used, along with more powerful un-binned non-parametric tests to compare the distribution of SSN for pandemic years to that of all years, no significant result was obtained with either the Wolf or Group sunspot numbers.











