Hostname: page-component-784d4fb959-wxg6b Total loading time: 0 Render date: 2025-07-14T20:17:10.893Z Has data issue: false hasContentIssue false
  • English
  • Français

On periodic motions of a two dimensional Toda type chain

Published online by Cambridge University Press:  15 December 2004

Gianni Mancini  and
P. N. Srikanth
Gianni Mancini
Affiliation:
Dipartimento di Mathematica, Universita di Roma Tre, Via S. Leonardo Murialdo 1, Roma, Italy; mancini@matrm3.mat.uniroma3.it
P. N. Srikanth
Affiliation:
TIFR Centre, IISc Campus, PB 1234, Bangalore – 560 012, India; srikanth@math.tifrbng.res.in
Get access

Abstract

In this paper we consider a chain of strings with fixed end points coupled with nearest neighbour interaction potential of exponential type, i.e. $$\left\{\begin{array}{l} \varphi^{i}_{tt} - \varphi^{i}_{xx} = \exp(\varphi^{i+1} -\varphi^{i}) - \exp( \varphi^{i} - \varphi{i-1} ) \quad 0<x<\pi, \quad t \in \rm I\hskip-1.8pt R, i \in Z\!\!\!Z\quad (TC) \varphi^i (0,t) = \varphi^i (\pi,t) = 0 \quad\forall t, i. \end{array}\right.$$ 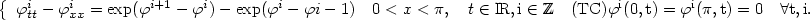We consider the case of “closed chains" i.e. $ \varphi^{i+N} = \varphi^i \forall i \in Z\!\!\!Z$ 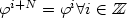and some $ N \in {I\!\!N}$ 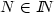and look for solutions which are peirodicin time. The existence of periodic solutions for the dual problem is proved in Orlicz space setting.

Keywords

PeriodicToda type chain.

Information

Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 11 , Issue 1 , January 2005 , pp. 72 - 87
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

R.A. Adams, Sobolev Spaces. A.P (1975).
Arnold, V.I., Proof of a Theorem of A.N. Kolmogorov on the invariance of quasi-periodic motions under small perturbations of the Hamiltonian. Russ. Math. Surv. 18 (1963) 9–36. CrossRef
H. Brezis and L. Nirenberg, Forced vibrations for a nonlinear wave equation. CPAM, XXXI(1) (1978) 1–30.
H. Brezis, J.M. Coron and L. Nirenberg, Free Vibrations for a Nonlinear Wave Equation and a Theorem of P. Rabinowitz. CPAM, XXXIII (1980) 667–684.
Friesecke, G. and Wattis Jonathan, A.D., Existence Theorem for Solitary Waves on Lattices. Commun. Math. Phys. 161 (1994) 391–418. CrossRef
Iooss, G., Travelling waves in the Fermi-Pasta-Ulam lattice. Nonlinearity 13 (2000) 849–866. CrossRef
M.A. Krasnoselsky and Y.B. Rutitsky, Convex Functions and Orlicz Spaces. Internat. Monogr. Adv. Math. Phys. Hindustan Publishing Corpn., India (1962).
Lovicarova', H., Periodic solutions of a weakly nonlinear wave equation in one dimension. Czechmath. J. 19 (1969) 324–342.
J. Moser, On invariant curves of area-preserving mappings of an annulus. Nachr. Akad. Wiss. Göttingen, K1 2 (1962) 1.
Mikhailov, A.V., Integrability of a Two-Dimensional Generalization of the Toda Chain. JETP Lett. 30 (1979) 414–413.
L. Nirenberg, Variational Methods in nonlinear problems. M. Giaquinta Ed., Springer-Verlag, Lect. Notes Math. 1365 (1987).
Rabinowitz, P.H., Periodic solutions of Hamiltonian Systems. Comm. Pure Appl. Math. 31 (1978) 157–184. CrossRef
Ruf, B. and Srikanth, P.N., On periodic Motions of Lattices of Toda Type via Critical Point Theory. Arch. Ration. Mech. Anal. 126 (1994) 369–385. CrossRef
M. Toda, Theory of Nonlinear Lattices. Springer-Verlag (1989).