Fix two points $x,\bar{x}\in S^2$ and two directions (without orientation) $\eta,\bar\eta$ 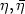of the velocities in these points. In this paper we are interested to the problem of minimizing the cost

$J[\gamma]=\int_0^T \left({\g}_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t))+ K^2_{\gamma(t)}{\g}_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t)) \right) ~{\rm d}t$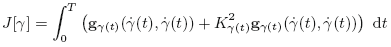

along all smooth curves starting from x with direction η and ending in $\bar{x}$ 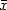with direction $\bar\eta$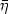. Here g is the standard Riemannian metric on S2 and $K_\gamma$ 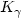is the corresponding geodesic curvature. The interest of this problem comes from mechanics and geometry of vision. It can be formulated as a sub-Riemannian problem on the lens space L(4,1). We compute the global solution for this problem: an interesting feature is that some optimal geodesics present cusps. The cut locus is a stratification with non trivial topology.