We develop the analysis of stabilized sparse tensor-product finite element methods for high-dimensional, non-self-adjoint and possibly degenerate second-order partial differential equations of the form $-a:\nabla\nabla u + b \cdot \nabla u + cu = f(x)$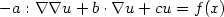, $x \in \Omega = (0,1)^d \subset \mathbb{R}^d$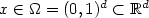, where $a \in \mathbb{R}^{d\times d}$ is a symmetric positive semidefinite matrix, using piecewise polynomials of degree p ≥ 1. Our convergence analysis is based on new high-dimensional approximation results in sparse tensor-product spaces. We show that the error between the analytical solution u and its stabilized sparse finite element approximation uh on a partition of Ω of mesh size h = hL = 2-L satisfies the following bound in the streamline-diffusion norm $|||\cdot|||_{\rm SD}$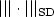, provided u belongs to the space $\mathcal{H}^{k+1}(\Omega)$ of functions with square-integrable mixed (k+1)st derivatives: \[ |||u-u_h|||_{\rm SD}\leq C_{p,t} d^2 \max\{(2-p)_+,\kappa_0^{d-1},\kappa_1^d\} (|\sqrt{a}| h_L^t + |b|^{\frac{1}{2}} h_L^{t+\frac{1}{2}} + c^{\frac{1}{2}} h_L^{t+1} \!)|u|_{\mathcal{H}^{t+1}(\Omega)}, \qquad \qquad \qquad 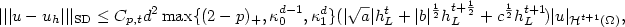\] where $\kappa_i=\kappa_i(p,t,L)$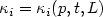, i=0,1, and $1 \leq t \leq \min(k,p)$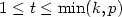. We show, under various mild conditions relating L to p, L to d, or p to d, that in the case of elliptic transport-dominated diffusion problems $\kappa_0, \kappa_1 \in (0,1)$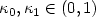, and hence for p ≥ 1 the 'error constant' $C_{p,t} d^2 \max\{(2-p)_+,\kappa_0^{d-1},\kappa_1^d\}$ 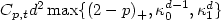exhibits exponential decay as d → ∞; in the case of a general symmetric positive semidefinite matrix a, the error constant is shown to grow no faster than $\mathcal{O}(d^2)$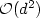. In any case, in the absence of assumptions that relate L, p and d, the error $|||u - u_h|||_{\rm SD}$ 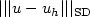is still bounded by $\kappa_\ast^{d-1} |\log_2 h_L|^{d-1}\mathcal{O}(|\sqrt{a}| h_L^t + |b|^{\frac{1}{2}} h_L^{t+\frac{1}{2}} + c^{\frac{1}{2}} h_L^{t+1})$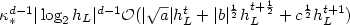, where $\kappa_\ast \in (0,1)$ 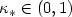for all L, p, d ≥ 2.