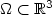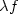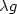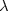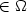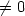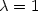Refine listing
Actions for selected content:
Contents
Research Article
Characterization of the limit load in the caseof an unbounded elastic convex
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 637-648
-
- Article
- Export citation
The numerical interface coupling of nonlinearhyperbolic systems of conservation laws: II. The case of systems
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 649-692
-
- Article
- Export citation
On the Schwarz algorithms for the Elliptic Exterior Boundary Value Problems
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 693-714
-
- Article
- Export citation
Iteratively solving a kind of signorinitransmission problem in a unbounded domain
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 715-726
-
- Article
- Export citation
Mixed discontinuous Galerkin approximationof the Maxwell operator: The indefinite case
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 727-753
-
- Article
- Export citation
Finite element approximation for degenerate parabolic equations. an application of nonlinear semigroup theory
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 755-780
-
- Article
- Export citation
Moving mesh for the axisymmetric harmonic map flow
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 781-796
-
- Article
- Export citation
Analysis of a prototypicalmultiscale method coupling atomistic and continuum mechanics
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 797-826
-
- Article
- Export citation
Generalized Newton methods for the 2D-Signorini contact problem with friction in function space
-
- Published online by Cambridge University Press:
- 15 August 2005, pp. 827-854
-
- Article
- Export citation