Article contents
A new kind of augmentation of filtrations
Published online by Cambridge University Press: 15 October 2010
Abstract
Let (Ω, $\mathcal{F}$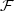 , ($\mathcal{F}_t$
, ($\mathcal{F}_t$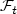 )t≥0, $\mathbb{P}$
)t≥0, $\mathbb{P}$ ) be a filtered probability space satisfying the usual assumptions: it is usually not possible to extend to $\mathcal{F}_{\infty}$
) be a filtered probability space satisfying the usual assumptions: it is usually not possible to extend to $\mathcal{F}_{\infty}$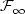 (the σ-algebra generated by ($\mathcal{F}_t$
(the σ-algebra generated by ($\mathcal{F}_t$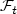 )t≥0) a coherent family of probability measures ($\mathbb{Q}_t$
)t≥0) a coherent family of probability measures ($\mathbb{Q}_t$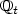 ) indexed by t ≥ 0, eachof them being defined on $\mathcal{F}_t$
) indexed by t ≥ 0, eachof them being defined on $\mathcal{F}_t$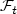 . It is known that for instance, on the Wiener space, this extension problem has a positive answer if one takes the filtration generated by the coordinate process, made right-continuous, but can have a negative answer if one takes its usual augmentation. On the other hand, the usual assumptions are crucial in order to obtain the existence of regular versions of paths (typically adapted and continuous or adapted and càdlàg versions) for most stochastic processes of interest, such as the local time of the standard Brownian motion, stochastic integrals, etc. For instance we shall prove that on the Wiener space, equipped with the right-continuous augmentation of the filtration generated by the canonical process, there exists no càdlàg or continuous and adapted version for the local time at level zero of the canonical process. Hence there is an incompatibility between the problem of extending a coherent family of probability measures to $\mathcal{F}_\infty$
. It is known that for instance, on the Wiener space, this extension problem has a positive answer if one takes the filtration generated by the coordinate process, made right-continuous, but can have a negative answer if one takes its usual augmentation. On the other hand, the usual assumptions are crucial in order to obtain the existence of regular versions of paths (typically adapted and continuous or adapted and càdlàg versions) for most stochastic processes of interest, such as the local time of the standard Brownian motion, stochastic integrals, etc. For instance we shall prove that on the Wiener space, equipped with the right-continuous augmentation of the filtration generated by the canonical process, there exists no càdlàg or continuous and adapted version for the local time at level zero of the canonical process. Hence there is an incompatibility between the problem of extending a coherent family of probability measures to $\mathcal{F}_\infty$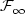 and the classical construction of regular versions of paths, requiring the usual assumptions (this situation typically occurs in the problem of penalization of the Brownian paths or in mathematical finance), which to the best of our knowledge, has not been noticed so far.In order to fix this problem, we introduce a new property for filtrations, intermediate between the right continuityand the usual conditions. More precisely, we say that a filtration ($\mathcal{F}_t$
and the classical construction of regular versions of paths, requiring the usual assumptions (this situation typically occurs in the problem of penalization of the Brownian paths or in mathematical finance), which to the best of our knowledge, has not been noticed so far.In order to fix this problem, we introduce a new property for filtrations, intermediate between the right continuityand the usual conditions. More precisely, we say that a filtration ($\mathcal{F}_t$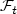 )t≥0 satisfies the natural assumptionsif it is right-continuous and if $\mathcal{F}_0$
)t≥0 satisfies the natural assumptionsif it is right-continuous and if $\mathcal{F}_0$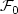 contains all the sets included in a countable unionof negligible sets (Bn)n≥1, such that Bn ∈ $\mathcal{F}_n$
contains all the sets included in a countable unionof negligible sets (Bn)n≥1, such that Bn ∈ $\mathcal{F}_n$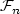 for n ≥ 1.There is a natural way to obtain, from a given filtration ($\mathcal{F}_t$
for n ≥ 1.There is a natural way to obtain, from a given filtration ($\mathcal{F}_t$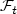 )t≥0, a new filtration which satisfies the natural assumptions: we call it the natural augmentation of ($\mathcal{F}_t$
)t≥0, a new filtration which satisfies the natural assumptions: we call it the natural augmentation of ($\mathcal{F}_t$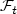 )t≥0.We show that most of the important results of the theory of stochastic processes which are generally proved under the usual augmentation, such as the existence of regular version of trajectories or the début theorem, still hold under the natural augmentation; moreover this new augmentation allows the extension of a coherent family of probability measures whenever this is possible with the original filtration. For sake of completeness, we also recall (not so well known) Parthasarathy type conditions on the underlying filtration under which the extension problem for a coherent family of probability measures has a solution. In particular, we shall see that this is always the case on the following two fundamental spaces: $\mathcal{C}$
)t≥0.We show that most of the important results of the theory of stochastic processes which are generally proved under the usual augmentation, such as the existence of regular version of trajectories or the début theorem, still hold under the natural augmentation; moreover this new augmentation allows the extension of a coherent family of probability measures whenever this is possible with the original filtration. For sake of completeness, we also recall (not so well known) Parthasarathy type conditions on the underlying filtration under which the extension problem for a coherent family of probability measures has a solution. In particular, we shall see that this is always the case on the following two fundamental spaces: $\mathcal{C}$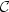 ($\mathbb{R}_+$
($\mathbb{R}_+$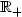 , $\mathbb{R}$
, $\mathbb{R}$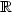 ), the space of continuous functions equipped with the filtration generated by the coordinate process and $\mathcal{D}$
), the space of continuous functions equipped with the filtration generated by the coordinate process and $\mathcal{D}$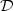 ($\mathbb{R}_+$
($\mathbb{R}_+$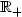 , $\mathbb{R}$
, $\mathbb{R}$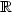 ), the space of càdlàg functions endowed with the filtration generated by the coordinate process.
), the space of càdlàg functions endowed with the filtration generated by the coordinate process.
Information
- Type
- Research Article
- Information
- ESAIM: Probability and Statistics , Volume 15: Supplement: In honor of Marc Yor , 2011 , pp. S39 - S57
- Copyright
- © EDP Sciences, SMAI, 2011
References
- 12
- Cited by

