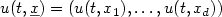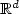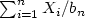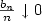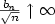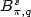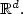Refine listing
Actions for selected content:
Contents
Research Article
The law of the iterated logarithmfor the multivariate kernel modeestimator
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 1-21
-
- Article
- Export citation
Superposition of Diffusions with Linear Generator and its Multifractal Limit Process
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 23-88
-
- Article
- Export citation
Positivity of the density for the stochasticwave equation in two spatial dimensions
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 89-114
-
- Article
- Export citation
Convergence of iterates of a transfer operator,application to dynamical systems and to Markov chains
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 115-146
-
- Article
- Export citation
Adaptive tests of qualitative hypotheses
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 147-159
-
- Article
- Export citation
About the linear-quadratic regulator problem under a fractional Brownian perturbation
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 161-170
-
- Article
- Export citation
Particle approximations of Lyapunov exponents connected to Schrödinger operators and Feynman–Kac semigroups
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 171-208
-
- Article
- Export citation
Moderate Deviations for I.I.D. Random Variables
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 209-218
-
- Article
- Export citation
Asymptotic behaviour of theprobability-weighted moments and penultimate approximation
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 219-238
-
- Article
- Export citation
Replicant compression coding in Besov spaces
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 239-250
-
- Article
- Export citation
Interacting Brownian particles and Gibbs fields on pathspaces
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 251-277
-
- Article
- Export citation
On Asymptotic Minimaxity of Kernel-based Tests
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 279-312
-
- Article
- Export citation
Constraints on distributions imposedby properties of linear forms
-
- Published online by Cambridge University Press:
- 15 May 2003, pp. 313-328
-
- Article
- Export citation