Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elliott, Charles M.
and
Garcke, Harald
1996.
On the Cahn–Hilliard Equation with Degenerate Mobility.
SIAM Journal on Mathematical Analysis,
Vol. 27,
Issue. 2,
p.
404.
Elliott, Charles M.
and
Garcke, Harald
1997.
Diffusional phase transitions in multicomponent systems with a concentration dependent mobility matrix.
Physica D: Nonlinear Phenomena,
Vol. 109,
Issue. 3-4,
p.
242.
Otto, Felix
and
E, Weinan
1997.
Thermodynamically driven incompressible fluid mixtures.
The Journal of Chemical Physics,
Vol. 107,
Issue. 23,
p.
10177.
March, Riccardo
and
Dozio, Marziano
1997.
A variational method for the recovery of smooth boundaries.
Image and Vision Computing,
Vol. 15,
Issue. 9,
p.
705.
Bronsard, Lia
Garcke, Harald
and
Stoth, Barbara
1998.
A multi-phase Mullins–Sekerka system: matched asymptotic expansions and an implicit time discretisation for the geometric evolution problem.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 128,
Issue. 3,
p.
481.
Escher, Joachim
Mayer, Uwe F.
and
Simonett, Gieri
1998.
The Surface Diffusion Flow for Immersed Hypersurfaces.
SIAM Journal on Mathematical Analysis,
Vol. 29,
Issue. 6,
p.
1419.
Giacomin, Giambattista
and
Lebowitz, Joel L.
1998.
Phase Segregation Dynamics in Particle Systems with Long Range Interactions II: Interface Motion.
SIAM Journal on Applied Mathematics,
Vol. 58,
Issue. 6,
p.
1707.
1998.
The Selected Works of John W. Cahn.
Bernoff, Andrew J.
Bertozzi, Andrea L.
and
Witelski, Thomas P.
1998.
Axisymmetric Surface Diffusion: Dynamics and Stability of Self-Similar Pinchoff.
Journal of Statistical Physics,
Vol. 93,
Issue. 3-4,
p.
725.
Choo, S.M.
and
Chung, S.K.
1998.
Conservative nonlinear difference scheme for the Cahn-Hilliard equation.
Computers & Mathematics with Applications,
Vol. 36,
Issue. 7,
p.
31.
Barrett, John W.
Blowey, James F.
and
Garcke, Harald
1999.
Finite Element Approximation of the Cahn--Hilliard Equation with Degenerate Mobility.
SIAM Journal on Numerical Analysis,
Vol. 37,
Issue. 1,
p.
286.
Escher, Joachim
and
Simonett, Gieri
1999.
Topics in Nonlinear Analysis.
p.
183.
Giga, Yoshikazu
and
Ito, Kazuo
1999.
Topics in Nonlinear Analysis.
p.
305.
Li, Zhilin
Zhao, Hongkai
and
Gao, Huajian
1999.
A Numerical Study of Electro-migration Voiding by Evolving Level Set Functions on a Fixed Cartesian Grid.
Journal of Computational Physics,
Vol. 152,
Issue. 1,
p.
281.
Yokojima, Y.
and
Shiwa, Y.
2000.
Ordering process in quenched block copolymers at low temperatures.
Physical Review E,
Vol. 62,
Issue. 5,
p.
6838.
Cahn, J.W.
and
Novick-Cohen, A.
2000.
Motion by curvature and impurity drag: resolution of a mobility paradox.
Acta Materialia,
Vol. 48,
Issue. 13,
p.
3425.
Thompson, J. M. T.
and
King, J. R.
2000.
Emerging areas of mathematical modelling.
Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 358,
Issue. 1765,
p.
3.
Novick-Cohen, A.
2000.
Triple-junction motion for an Allen–Cahn/Cahn–Hilliard system.
Physica D: Nonlinear Phenomena,
Vol. 137,
Issue. 1-2,
p.
1.
Bhate, Deepali N.
Kumar, Ashish
and
Bower, Allan F.
2000.
Diffuse interface model for electromigration and stress voiding.
Journal of Applied Physics,
Vol. 87,
Issue. 4,
p.
1712.
Hulshof, J.
King, J. R.
and
Bowen, M.
2001.
Anomalous Exponents and Dipole Solutions for the Thin Film Equation.
SIAM Journal on Applied Mathematics,
Vol. 62,
Issue. 1,
p.
149.


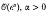 where є
where є