Article contents
A contact problem for viscoelastic bodies with inertial effects and unilateral boundary constraints
Published online by Cambridge University Press: 07 March 2016
Abstract
We consider a viscoelastic body occupying a smooth bounded domain 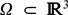 $\Omega\subset \mathbb{R}^3$ under the effect of a volumic traction force g . The macroscopic displacement vector from the equilibrium configuration is denoted by u. Inertial effects are considered; hence, the equation for u contains the second-order term u tt . On a part ΓD of the boundary of Ω, the body is fixed and no displacement may occur; on a second part Γ N ⊂ ∂Ω, the body can move freely; on a third portion Γ C ⊂ ∂Ω, the body is in adhesive contact with a solid support. The boundary forces acting on ΓC due to the action of elastic stresses are responsible for delamination, i.e., progressive failure of adhesive bonds. This phenomenon is mathematically represented by a non-linear ordinary differential equation settled on ΓC and describing the evolution of the delamination order parameter z. Following the lines of a new approach outlined in Bonetti et al. (2015, arXiv:1503.01911) and based on duality methods in Sobolev–Bochner spaces, we define a suitable concept of weak solution to the resulting system of partial differential equations. Correspondingly, we prove an existence result on finite-time intervals of arbitrary length.
$\Omega\subset \mathbb{R}^3$ under the effect of a volumic traction force g . The macroscopic displacement vector from the equilibrium configuration is denoted by u. Inertial effects are considered; hence, the equation for u contains the second-order term u tt . On a part ΓD of the boundary of Ω, the body is fixed and no displacement may occur; on a second part Γ N ⊂ ∂Ω, the body can move freely; on a third portion Γ C ⊂ ∂Ω, the body is in adhesive contact with a solid support. The boundary forces acting on ΓC due to the action of elastic stresses are responsible for delamination, i.e., progressive failure of adhesive bonds. This phenomenon is mathematically represented by a non-linear ordinary differential equation settled on ΓC and describing the evolution of the delamination order parameter z. Following the lines of a new approach outlined in Bonetti et al. (2015, arXiv:1503.01911) and based on duality methods in Sobolev–Bochner spaces, we define a suitable concept of weak solution to the resulting system of partial differential equations. Correspondingly, we prove an existence result on finite-time intervals of arbitrary length.
Keywords
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2016
References
- 7
- Cited by

