Article contents
Homogenization of a non-stationary non-Newtonian flow in a porous medium containing a thin fissure
Published online by Cambridge University Press: 05 February 2018
Abstract
We consider a non-stationary incompressible non-Newtonian Stokes system in a porous medium with characteristic size of the pores ϵ and containing a thin fissure of width ηϵ. The viscosity is supposed to obey the power law with flow index 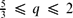 $\frac{5}{3}\leq q\leq 2$. The limit when size of the pores tends to zero gives the homogenized behaviour of the flow. We obtain three different models depending on the magnitude ηϵ with respect to ϵ: if ηϵ ≪
$\frac{5}{3}\leq q\leq 2$. The limit when size of the pores tends to zero gives the homogenized behaviour of the flow. We obtain three different models depending on the magnitude ηϵ with respect to ϵ: if ηϵ ≪ 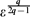 $\varepsilon^{q\over 2q-1}$ the homogenized fluid flow is governed by a time-dependent non-linear Darcy law, while if ηϵ ≫
$\varepsilon^{q\over 2q-1}$ the homogenized fluid flow is governed by a time-dependent non-linear Darcy law, while if ηϵ ≫ 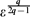 $\varepsilon^{q\over 2q-1}$ is governed by a time-dependent non-linear Reynolds problem. In the critical case, ηϵ ≈
$\varepsilon^{q\over 2q-1}$ is governed by a time-dependent non-linear Reynolds problem. In the critical case, ηϵ ≈ 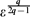 $\varepsilon^{q\over 2q-1}$, the flow is described by a time-dependent non-linear Darcy law coupled with a time-dependent non-linear Reynolds problem.
$\varepsilon^{q\over 2q-1}$, the flow is described by a time-dependent non-linear Darcy law coupled with a time-dependent non-linear Reynolds problem.
Keywords
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2018
References
- 9
- Cited by

