No CrossRef data available.
Article contents
Analysis of 2 + 1 diffusive–dispersive PDE arising in river braiding
Published online by Cambridge University Press: 16 February 2016
Abstract
We present local existence and uniqueness results for the following 2 + 1 diffusive–dispersive equation due to P. Hall arising in modelling of river braiding: for (x,y) ∈ [0, 2π] × [0, π], t > 0, with boundary condition u y =0=u yyy at y=0 and y=π and 2π periodicity in x, using a contraction mapping argument in a Bourgain-type space T s,b . We also show that the energy ∥u(·, ·, t)∥2 L2 and cumulative dissipation ∫0 t ∥u y (·, ·, s)∥L2 2 dt are globally controlled in time t.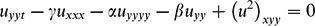 $$\begin{equation*} u_{yyt} - \gamma u_{xxx} -\alpha u_{yyyy} - \beta u_{yy} + \left ( u^2 \right )_{xyy} = 0 \end{equation*}$$
$$\begin{equation*} u_{yyt} - \gamma u_{xxx} -\alpha u_{yyyy} - \beta u_{yy} + \left ( u^2 \right )_{xyy} = 0 \end{equation*}$$
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2016
References
[1]
Angelopoulos, Y. (2013) Well-posedness and ill-posedness results for the Novikov-Veselov equation, preprint, ArXiv:1307.4110.Google Scholar
[2]
Angulo, J., Matheus, C. & Pilod, D. (2009) Global well-posedness and non-linear stability of periodic traveling waves for a Schrödinger-Benjamin-Ono system. Commun. Pure Appl. Anal.
8
(3), 815–844. MR2476660CrossRefGoogle Scholar
[3]
Bourgain, J. (1993) Fourier transform restriction phenomena for certain lattice subsets and application to nonlinear evolution equations I. Schrödinger equations. Geom. Funct. Anal.
3
(2), 107–156. MR1209299 (95d:35160a)CrossRefGoogle Scholar
[4]
Bourgain, J. (1993) Fourier transform restriction phenomena for certain lattice subsets and application to nonlinear evolution equations II. The KdV equation. Geom. Funct. Anal.
3
(3), 209–262. MR1215780 (95d:35160b)Google Scholar
[5]
Bourgain, J. (1993) On the Cauchy problem for the Kadomstev-Petviashvili equation. Geom. Funct. Anal.
3
(4), 315–341. MR1223434 (94d:35142)CrossRefGoogle Scholar
[6]
Chen, R., Liu, Y. & Zhang, P. (2012) Local regularity and decay estimates of solitary waves for the rotation-modified Kadomtsev-Petviashvili equation. Trans. Am. Math. Soc.
364
(7), 3395–3425. MR2901218CrossRefGoogle Scholar
[7]
Chen, W. & Li, J. (2007) On the low regularity of the modified Korteweg-de Vries equation with a dissipative term. J. Differ. Equ.
240
(1), 125–144. MR2349167 (2008g:35182)Google Scholar
[8]
Chen, W. & Li, J. (2008) On the low regularity of the Benney-Lin equation. J. Math. Anal. Appl.
339
(2), 1134–1147. MR2377072 (2009e:35228)CrossRefGoogle Scholar
[9]
Chen, W., Li, J. & Miao, C. (2007) On the well-posedness of the Cauchy problem for dissipative modified Korteweg-de Vries equations. Differ. Integral Equ.
20
(11), 1285–1301. MR2372427 (2008k:35401)Google Scholar
[10]
Chen, W., Li, J. & Miao, C. (2008) On the low regularity of the fifth order Kadomtsev-Petviashvili I equation. J. Differ. Equ.
245
(11), 3433–3469. MR2460030 (2009j:35302)CrossRefGoogle Scholar
[11]
Darwich, M. (2012) On the well-posedness for Kadomtsev-Petviashvili-Burgers I equation. J. Differ. Equ.
253
(5), 1584–1603. MR2927391CrossRefGoogle Scholar
[12]
Esfahani, A. (2012) The ADMB-KdV equation in Anisotropic Sobolev spaces. Differ. Equ. Appl.
4
(3), 459–484. MR3012073Google Scholar
[13]
Hadac, M. (2008) Well-Posedness for the Kadomtsev-Petviashvili II equation and generalisations. Trans. Am. Math. Soc.
360
(12), 6555–6572. MR2434299 (2009g:35265)CrossRefGoogle Scholar
[14]
Hall, P. (2006) Nonlinear evolution equations and braiding of weakly transporting flows over gravel beds. Stud. Appl. Math.
117
(1), 27–69. MR2236577 (2007c:76034)Google Scholar
[15]
Kenig, C. E., Ponce, G. & Vega, L. (1991) Well-posedness of the initial value problem for the Korteweg-de Vries equation. J. Am. Math. Soc.
4
(2), 323–347. MR1086966 (92c:35106)CrossRefGoogle Scholar
[16]
Kenig, C. E., Ponce, G. & Vega, L. (1996) A bilinear estimate with applications to the KdV equation. J. Am. Math. Soc.
9
(2), 573–603. MR1329387 (96k:35159)CrossRefGoogle Scholar
[17]
Kojok, B. (2007) Sharp well-posedness for Kadomtsev-Petviashvili-Burgers (KBII) equation in R
2
. J. Differ. Equ.
242
(2), 211–247. MR2363314 (2009b:35363)Google Scholar
[18]
Molinet, L. & Ribaud, F. (2002) On the low regularity of the Kortewig-de Vries-Burgers equation. Int. Math. Res. Not.
37, 1979–2005. MR1918236 (2003e:35272)CrossRefGoogle Scholar
[19]
Otani, M. (2006) Well-posedness of the generalized Benjamin-Ono-Burgers equations in Sobolev spaces of negative order. Osaka J. Math.
43
(4), 935–965. MR2303557 (2008d:35202)Google Scholar
[20]
Pecher, H. (2012) Some new well-posedness results for the Klein-Gordon-Schrödinger system. Differ. Integral Equ.
25
(1–2), 117–142. MR2906550 (2012m:35310)Google Scholar
[21]
Tao, T. (2006) Nonlinear Dispersive Equations: Local and Global Analysis}. CBMS Regional Conference Series in Mathematics, 106. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 2006. xvi+373 pp. ISBN: 0-8218-4143-2.Google Scholar

