Article contents
Analysis of a heterogeneous model for riot dynamics: the effect of censorship of information
Published online by Cambridge University Press: 15 July 2015
Abstract
This paper is concerned with modelling the dynamics of social outbursts of activity, such as protests or riots. In this sequel to our work in Berestycki et al. (Networks and Heterogeneous Media, vol. 10, no. 3, 1–34), written in collaboration with J-P. Nadal, we model the effect of restriction of information and explore its impact on the existence of upheaval waves. The system involves the coupling of an explicit variable representing the intensity of rioting activity and an underlying (implicit) field of social tension. We prove the existence of global solutions to the Cauchy problem in 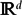 ${\mathbb R}^d$ as well as the existence of traveling wave solutions in certain parameter regimes. We furthermore explore the effects of heterogeneities in the environment with the help of numerical simulations, which lead to pulsating waves in certain cases. We analyse the effects of periodic domains as well as the barrier problem with the help of numerical simulations. The barrier problem refers to the potential blockage of a wavefront due to a spatial heterogeneity in the system which leads to an area of low excitability (referred to as the barrier). We conclude with a variety of open problems.
${\mathbb R}^d$ as well as the existence of traveling wave solutions in certain parameter regimes. We furthermore explore the effects of heterogeneities in the environment with the help of numerical simulations, which lead to pulsating waves in certain cases. We analyse the effects of periodic domains as well as the barrier problem with the help of numerical simulations. The barrier problem refers to the potential blockage of a wavefront due to a spatial heterogeneity in the system which leads to an area of low excitability (referred to as the barrier). We conclude with a variety of open problems.
Keywords
Information
- Type
- Papers
- Information
- European Journal of Applied Mathematics , Volume 27 , Issue 3: Mathematical Modelling of Crime and Security , June 2016 , pp. 554 - 582
- Copyright
- Copyright © Cambridge University Press 2015
References
- 9
- Cited by

