Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Abdulla, Ugur G.
Du, Jian
Prinkey, Adam
Ondracek, Chloe
and
Parimoo, Suneil
2018.
Evolution of interfaces for the nonlinear double degenerate parabolic equation of turbulent filtration with absorption.
Mathematics and Computers in Simulation,
Vol. 153,
Issue. ,
p.
59.
Liu, Yang
Yu, Tao
and
Li, Wenke
2020.
Global well-posedness, asymptotic behavior and blow-up of solutions for a class of degenerate parabolic equations.
Nonlinear Analysis,
Vol. 196,
Issue. ,
p.
111759.
ABDULLA, UGUR G.
and
JELI, ROQIA
2020.
Evolution of interfaces for the nonlinear parabolic p-Laplacian-type reaction-diffusion equations. II. Fast diffusion vs. absorption.
European Journal of Applied Mathematics,
Vol. 31,
Issue. 3,
p.
385.
Abdulla, Ugur G.
and
Abuweden, Amna
2020.
Interface development for the nonlinear degenerate multidimensional reaction–diffusion equations.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 27,
Issue. 1,
Rong, Mei
Miao, Qing
and
Jaballah, Ali
2022.
A Sub‐Supersolution Method for p‐Laplacian Equation with Non‐Local Term.
Journal of Mathematics,
Vol. 2022,
Issue. 1,
Efendiev, Messoud A.
Ôtani, Mitsuharu
and
Eberl, Hermann J.
2022.
Long time behavior of a parabolic p-Laplacian equation coupled to a compartmental ODE system with an induction threshold phenomenon.
Journal of Differential Equations,
Vol. 339,
Issue. ,
p.
602.
Abdulla, Ugur G.
and
Abu Weden, Amna
2023.
Interface development for the nonlinear degenerate multidimensional reaction–diffusion equations II: fast diffusion versus absorption.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 30,
Issue. 3,
Aal-Rkhais, Habeeb A.
and
Qasim, Ruba H.
2024.
Asymptotic behaviour for a parabolic p-Laplacian equation with an advection force.
Journal of Physics: Conference Series,
Vol. 2701,
Issue. 1,
p.
012120.
Jeli, Roqia Abdullah
and
Makinde, Oluwole D.
2025.
Development of Interfaces in Nonlinear Multidimensional Reaction‐Diffusion Equations With Parabolic p‐Laplacian Properties.
Journal of Applied Mathematics,
Vol. 2025,
Issue. 1,
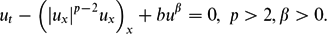 $$\begin{equation*}u_t-\Big(|u_x|^{p-2}u_x\Big)_x+bu^{\beta}=0, \ p>2, \beta >0.\end{equation*}$$
$$\begin{equation*}u_t-\Big(|u_x|^{p-2}u_x\Big)_x+bu^{\beta}=0, \ p>2, \beta >0.\end{equation*}$$ 
