Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T19:23:26.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogenization of a non-stationary non-Newtonian flow in a porous medium containing a thin fissure

Published online by Cambridge University Press:  05 February 2018

MARÍA ANGUIANO
MARÍA ANGUIANO*
Affiliation:
Departamento de Análisis Matemático, Facultad de Matemáticas, Universidad de Sevilla, P. O. Box 1160, 41080-Sevilla, Spain email: anguiano@us.es
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a non-stationary incompressible non-Newtonian Stokes system in a porous medium with characteristic size of the pores ϵ and containing a thin fissure of width ηϵ. The viscosity is supposed to obey the power law with flow index 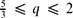$\frac{5}{3}\leq q\leq 2$. The limit when size of the pores tends to zero gives the homogenized behaviour of the flow. We obtain three different models depending on the magnitude ηϵ with respect to ϵ: if ηϵ ≪ 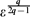$\varepsilon^{q\over 2q-1}$ the homogenized fluid flow is governed by a time-dependent non-linear Darcy law, while if ηϵ ≫ 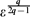$\varepsilon^{q\over 2q-1}$ is governed by a time-dependent non-linear Reynolds problem. In the critical case, ηϵ ≈ 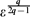$\varepsilon^{q\over 2q-1}$, the flow is described by a time-dependent non-linear Darcy law coupled with a time-dependent non-linear Reynolds problem.

Keywords

Non-Newtonian flowNon-stationary Stokes equationDarcy–Reynolds equationporous mediumfissure
Type
Papers
Information
European Journal of Applied Mathematics , Volume 30 , Issue 2 , April 2019 , pp. 248 - 277
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Allaire, G. (1989) Homogenization of the Stokes flow in a connected porous medium. Asymptot. Anal. 2, 203–222.Google Scholar
[2] Allaire, G. (1992) Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518.Google Scholar
[3] Bourgeat, A., ElAmri, H. & Tapiero, R. (1991) Existence d'une taille critique pour une fissure dans un milieu poreux. Second Colloque Franco Chilien de Mathematiques Appliquées, Cepadués Edts, Tolouse, 67–80.Google Scholar
[4] Bourgeat, A. & Tapiero, R. (1993) Homogenization in a perforated domain including a thin full interlayer. Int. Ser. Num. Math. 114, 25–36.Google Scholar
[5] Bourgeat, A., Marušic-Paloka, E. & Mikelić, A. (1995) Effective fluid flow in a porous medium containing a thin fissure. Asymptot. Anal. 11, 241–262.Google Scholar
[6] Bourgeat, A. & Mikelić, A. (1996) Homogenization of a polymer flow through a porous medium. Nonlinear Anal. 26, 1221–1253.Google Scholar
[7] Bourgeat, A., Gipouloux, O. & Marušić-Paloka, E. (2003) Filtration law for polymer flow through porous media. Multiscale Model. Simul. 1, 432–457.Google Scholar
[8] Clopeau, T. & Mikelić, A. (1998) On the non-stationary quasi-Newtonian flow through a thin slab. In: Navier–Stokes Equations: Theory and Numerical Methods, Pitman Res. Notes Math. Ser., 288, Longman, Harlow.Google Scholar
[9] Cloud, J. E. & Clark, P. E. (1985) Alternatives to the power-law fluid model for crosslinked fluids. Soc. Pet. Eng. J. 935-942.Google Scholar
[10] Galdi, G. P. 1994 An introduction to the mathematical theory of the Navier–Stokes equations, Springer-Verlag.Google Scholar
[11] Lions, J. L. 1969 Quelques méthodes de résolution des problèmes aux limites non linéaires, Dunod, Gauthier-Villars, Paris.Google Scholar
[12] Mikelić, A. & Tapiéro, R. (1995) Mathematical derivation of the power law describing polymer flow through a thin slab. RAIRO-Model. Math. Anal. Num. 29, 3–21.Google Scholar
[13] Nguestseng, G. (1989) A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20, 608–623.Google Scholar
[14] Panasenko, G. P. (1981) Higher order asymptotics of solutions of problems on the contact of periodic structures. Math. U.S.S.R. Sbornik 38, 465–494.Google Scholar
[15] Pham Huy, H. & Sanchez-Palencia, E. (1974) Phénomènes de transmission à travers des couches minces de conductivité élevée. J. Math. Anal. Appl. 47, 284–309.Google Scholar
[16] Shah, S. N. (1982) Propant settling correlations for non-Newtonian fluids under static and dynamic conditions. Soc. Pet. Eng. J., 164–170.Google Scholar
[17] Tartar, L. 1980 Incompressible fluid flow in a porous medium convergence of the homogenization process. Appendix to Lecture Notes in Physics, 127, Springer-Velag, Berlin.Google Scholar
[18] Temam, R. 1983 Navier-Stokes equations and nonlinear functional analysis. CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 41, Society for Industrial and Applied Mathematics (SIAM), Philadelphia.Google Scholar
[19] Zhao, H. & Yao, Z. (2008) Homogenization of a non-stationary Stokes flow in porous medium including a layer. J. Math. Anal. Appl. 342, 108–124.Google Scholar
[20] Zhao, H. & Yao, Z. (2012) Effective models of the Navier–Stokes flow in porous media with a thin fissure. J. Math. Anal. Appl. 387, 542–555.Google Scholar