Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T00:18:33.666Z Has data issue: false hasContentIssue false
  • English
  • Français

On continuous branches of very singular similarity solutions of a stable thin film equation. I – The Cauchy problem

Published online by Cambridge University Press:  21 February 2011

J. D. EVANS  and
V. A. GALAKTIONOV
J. D. EVANS
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath, BA2 7AY, UK email: masjde@maths.bath.ac.uk, vag@maths.bath.ac.uk
V. A. GALAKTIONOV
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath, BA2 7AY, UK email: masjde@maths.bath.ac.uk, vag@maths.bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the fourth-order thin film equation,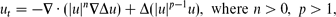with a stable second-order diffusion term. For the first critical exponent,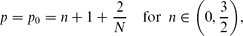where N ≥ 1 is the space dimension, the Cauchy problem is shown to admit countable continuous branches of source-type self-similar very singular solutions of the form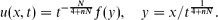These solutions are inherently oscillatory in nature and will be shown in Part II to be the limit of appropriate free-boundary problem solutions. For p ≠ p0, the set of very singular solutions is shown to be finite and to be consisting of a countable family of branches (in the parameter p) of similarity profiles that originate at a sequence of critical exponents {pl, l ≥ 0}. At p = pl, these branches appear via a non-linear bifurcation mechanism from a countable set of similarity solutions of the second kind of the pure thin film equation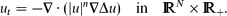Such solutions are detected by the ‘Hermitian spectral theory’, which allows an analytical n-branching approach. As such, a continuous path as n → 0+ can be constructed from the eigenfunctions of the linear rescaled operator for n = 0, i.e. for the bi-harmonic equation ut = −Δ2u. Numerics are used, wherever appropriate, to support the analysis.

Keywords

Stable thin film equationCauchy problemGlobal similarity solutionsAsymptotic behaviourBranchingBifurcationsHermitian spectral theory

Information

Type
Papers
Information
European Journal of Applied Mathematics , Volume 22 , Issue 3 , June 2011 , pp. 217 - 243
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Bernis, F. (1988) Source-type solutions of fourth order degenerate parabolic equations. In: Ni, W.-M., Peletier, L. A. & Serrin, J. (editors), Proc. Microprogram Nonlinear Diffusion Eqs Equilibrium States, Vol. 1, MSRI Publications, New York, NY, USA, pp. 123–146.CrossRefGoogle Scholar
[2]Bernis, F. & Friedman, A. (1990) Higher order nonlinear degenerate parabolic equations. J. Differ. Equ. 83, 179–206.CrossRefGoogle Scholar
[3]Bernis, F., Hulshof, J. & King, J. R. (2000) Dipoles and similarity solutions of the thin film equation in the half-line. Nonlinearity 13, 413–439.CrossRefGoogle Scholar
[4]Bernis, F. & McLeod, J. B. (1991) Similarity solutions of a higher order nonlinear diffusion equation. Nonlinear Anal. 17, 1039–1068.CrossRefGoogle Scholar
[5]Bernis, F., Peletier, L. A. & Williams, S. M. (1992) Source-type solutions of a fourth order nonlinear degenerate parabolic equation. Nonlinear Anal. Theory Methods Appl. 18, 217–234.CrossRefGoogle Scholar
[6]Bowen, M., Hulshof, J. & King, J. R. (2001) Anomalous exponents and dipole solutions for the thin film equation. SIAM J. Appl. Math. 62, 149–179.Google Scholar
[7]Bowen, M. & Witelski, T. P. (2006) The linear limit of the dipole problem for the thin film equation. SIAM J. Appl. Math. 66, 1727–1748.CrossRefGoogle Scholar
[8]Egorov, Yu. V., Galaktionov, V. A., Kondratiev, V. A. & Pohozaev, S. I. (2004) Asymptotic behaviour of global solutions to higher-order semilinear parabolic equations in the supercritical range. Adv. Difference Equ. 9, 1009–1038.Google Scholar
[9]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007a) Blow-up similarity solutions of the fourth-order unstable thin film equation. Eur. J. Appl. Math. 18, 195–231.CrossRefGoogle Scholar
[10]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007b) Source-type solutions for the fourth-order unstable thin film equation. Eur. J. Appl. Math. 18, 273–321.CrossRefGoogle Scholar
[11]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007c) Unstable sixth-order thin film equation. I. Blow-up similarity solutions; II. Global similarity patterns. Nonlinearity 20, 1799–1841, 1843–1881.CrossRefGoogle Scholar
[12]Evans, J. D., Galaktionov, V. A. & Williams, J. F. (2006) Blow-up and global asymptotics of the limit unstable Cahn–Hilliard equation. SIAM J. Math. Anal. 38, 64–102.CrossRefGoogle Scholar
[13]Ferreira, R. & Bernis, F. (1997) Source-type solutions to thin-film equations in higher dimensions. Eur. J. Appl. Math. 8, 507–534.CrossRefGoogle Scholar
[14]Galaktionov, V. A. (2004) Evolution completeness of separable solutions of non-linear diffusion equations in bounded domains. Math. Methods Appl. Sci. 27, 1755–1770.CrossRefGoogle Scholar
[15]Galaktionov, V. A. (2007) Sturmian nodal set analysis for higher-order parabolic equations and applications. Adv. Difference Equ. 12, 669–720.Google Scholar
[16]Galaktionov, V. A. (2010) Very singular solutions for thin film equations with absorption. Studies Appl. Math. 124, 39–63 (arXiv:0109.3982).CrossRefGoogle Scholar
[17]Galaktionov, V. A. & Harwin, P. J. (2005a) On evolution completeness of nonlinear eigenfunctions for the porous medium equation in the whole space. Adv. Difference Equ. 10, 635–674.Google Scholar
[18]Galaktinov, V. A. & Harwin, P. J. (2005b) Non-uniqueness and global similarity solutions for a higher-order semilinear parabolic equation. Nonlinearity 18, 717–746.CrossRefGoogle Scholar
[19]Galaktionov, V. A. & Harwin, P. J. (2009) On centre subspace behaviour in thin film equations. SIAM J. Appl. Math. 69, 1334–1358 (an earlier preprint in arXiv:0901.3995v1).CrossRefGoogle Scholar
[20]Galaktionov, V. A. & Svirshchevskii, S. R. (2007) Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics, Chapman & Hall/CRC, Boca Raton, FL, USA.Google Scholar
[21]Galaktionov, V. A. & Williams, J. F. (2004) On very singular similarity solutions of a higher-order semilinear parabolic equation. Nonlinearity 17, 1075–1099.CrossRefGoogle Scholar
[22]Gohberg, I., Goldberg, S. & Kaashoek, M. A. (1990) Classes of Linear Operators, Vol. 1; Operator Theory: Advances and Applications, Vol. 49, Birkhäuser Verlag, Basel, Switzerland/Berlin, Germany.Google Scholar
[23]Hulshof, J. (1991) Similarity solutions of the porous medium equation with sign changes. J. Math. Anal. Appl. 157, 75–111.CrossRefGoogle Scholar
[24]Kolmogorov, A. N. & Fomin, S. V. (1976) Elements of the Theory of Functions and Functional Analysis, Nauka, Moscow, Russia.Google Scholar
[25]Krasnosel'skii, M. A. & Zabreiko, P. P. (1984) Geometrical Methods of Nonlinear Analysis, Springer-Verlag, Berlin, Germany.CrossRefGoogle Scholar
[26]Perko, L. (1991) Differential Equations and Dynamical Systems, Springer-Verlag, New York, USA.CrossRefGoogle Scholar
[27]Vainberg, M. A. & Trenogin, V. A. (1974) Theory of Branching of Solutions of Non-Linear Equations, Noordhoff International Publishing, Leiden, Netherlands.Google Scholar
[28]Wu, Z., Zhao, J., Yin, J. & Li, H. (2001) Nonlinear Diffusion Equations, World Scientific Publishing Company, River Edge, NJ, USA.CrossRefGoogle Scholar
[29]Zel'dovich, Ya. B. (1956) The motion of a gas under the action of a short-term pressure shock. Akust. Zh., 2, 28–38; Sov. Phys. Acoust. 2, 25–35.Google Scholar